機器學習之異常檢測

前言

           以下內容是個人學習之后的感悟，轉載請注明出處~ 

 

 

簡介

　　在生活中，經常會遇到這樣一個對象集，有個別的對象是與大部分對象不一樣的，且前者是比較罕見的。我們通常

需要去發現它，這就用到了非監督學習的異常檢測算法，下面來舉一些異常檢測的應用：

• 欺騙檢測
• 制造業質檢
• 動力環境監測
• .........

　　異常檢測算法一般有以下幾種：

• 基於模型的技術：

　　　　許多異常檢測技術首先建立一個數據模型，異常是那些同模型不能完美擬合的對象。例如，數據分布的模型可以

　　通過估計概率分布的參數來創建。如果一個對象不服從該分布，則認為他是一個異常。

• 基於鄰近度的技術：

　　　　通常可以在對象之間定義鄰近性度量，異常對象是那些遠離大部分其他對象的對象。當數據能夠以二維或者三維散

　　布圖呈現時，可以從視覺上檢測出基於距離的離群點。

• 基於密度的技術：

　　　　對象的密度估計可以相對直接計算，特別是當對象之間存在鄰近性度量。低密度區域中的對象相對遠離近鄰，可能

　　被看做為異常。

 

異常檢測算法分析

　　本文以基於模型的高斯分布異常檢測算法為例，講解異常檢測的實現。

　　高斯分布，又名正態分布，其均值為μ、 方差為σ²的概率密度函數如下公式所示，如果一個隨機變量X服從這個分布，我們寫

作 X ~ N(μ,σ²)。此外，改變μ和σ，會使高斯分布曲線發生變化，其規律如下圖所示：

                                                                                

                                                                            

　　 首先，我們假設有一個數據集{x⁽¹⁾,x⁽²⁾,x⁽³⁾,.........,x^(m)}，其數據符合高斯分布，即 x⁽ⁱ⁾~ N(μ,σ²)，那么我們可以得到如下公式：

　　　　　　　　　　　　　　　　　

　　根據數據集，可得出訓練集：

　　　　　　　　　　　　　　　　　

　　利用上述訓練集，求出每個特征對應的μ_j和σ_j，即可得到每個特征的概率密度函數p(x_j;μ_j,σ_j)，然后建立出異常檢測模型：

                                                                            

　　最后取需要進行異常檢測的數據，代入上述的模型公式，若p(x)<ε，則為異常值。

　　這里對異常檢測算法的實現步驟做一下總結：

                                                         

 

 

評估異常檢測算法

　　我們采用的是查准率/召回率結合F-Score的評估方法，數據集分為訓練集、驗證集和測試集，這些都在之前學過的

機器學習之模型選擇與改進中講過，這里就不再贅述。

　　注意：ε值的選擇一般來說得靠經驗，或者可以選擇不同的ε值，通過評估方法來選擇最合適的值。

 

異常檢測VS監督學習

　　異常檢測的思想就是選出異類，其本質是分類，那么和監督學習相比，有什么區別呢？其區別如下圖所示，總結的來說，

無非是當異常檢測時，往往是異常點非常少的時候，根本無法用於監督學習，這也是使用異常檢測的原因所在。

                                           

 

設計特征

　　上面提到的高斯分布異常檢測算法，之所以能夠達到我們想要的效果，是因為在數據集的特征都符合高斯分布的前提下，

一旦分布規律偏差很大，效果就會很差。所以我們需要對不滿足高斯分布的特征進行重新設計，讓其符合高斯分布,一般可以

通過對數轉（log(x)）進行轉換。例如：

                 

　　有時候我們還需要根據實際應用情況設計新的特征變量來幫助異常檢測算法更好的檢測離群點。舉個檢測網絡系統的例子來

看看怎樣設計出更合理的特征：

                                                            

 

多元高斯分布

　　多元高斯分布有其優點也有其局限性，我們先來看看其優點。其優點是能夠捕捉到上面模型捕捉不到的異常樣本，

來看一個例子：

（1）我們的原始數據為下圖所示（圖左為二維的數據，圖右為把兩個特征分別當做高斯分布來建模）

                                               

 

（2）假如有個異常點（綠色樣本點）如下圖左中所示，其在下圖右中的檢測情況為：

                                              

 

　　從上圖能夠看出，這個綠色的異常樣本在單獨建模的模型中並不能檢測出來。因此這就需要通過多元高斯分布構

建模型來檢測。 多元高斯分布的概率密度函數為：

                                            

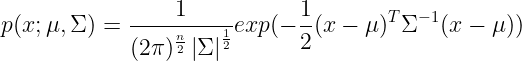
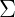　　其中為n*n維協方差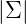矩陣，為矩陣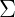的行列式。

　　下面我們來看一些例子，來說明向量和矩陣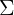對概率密度函數的影響。 先來看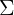的影響：

                                                

                                                                                                     圖一

                                                    

                                                                                                      圖二

                                                         

                                                                                                      圖三

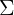　　從上面三個圖中可以看出當矩陣的副對角線都為0時，主對角線上的元素大小控制着概率密度函數俯瞰圖的形狀

大小，至於具體到數字大小對應的形狀，大家自己觀察便知。

　　再來看看主對角線不變，變化副對角線是如何影響的例子：

                                                       

                                                                                                    圖四

                                                          

                                                                                                      圖五  

　　能夠看出，副對角線控制的是傾斜程度。

　　下面來看看對概率密度函數的影響：

                                                          

　　從上圖能夠看出控制着圖形的位置變化。

 

 

多元高斯分布在異常檢測上的應用

　　介紹完多元高斯分布，下面我們來介紹下通過多元高斯分布推導出來的異常檢測算法：

                                                            

　　下面我們來看下多元高斯分布模型與多個一元高斯模型之間的關系：

                                                               

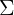　　其實就是當多元高斯分布模型的協方差矩陣為對角矩陣，且對角線上的元素為各自一元高斯分布模型的方差時，

二者是等價的。 下面來總結比較下多元高斯分布模型和多個一元高斯分布模型：

                                                              

 

 

 

以上是全部內容，如果有什么地方不對，請在下面留言，謝謝~