Neural Networks and Deep Learning(神經網絡與深度學習) - 學習筆記

catalogue

0. 引言
1. 感知器及激活函數
2. 代價函數(loss function)
3. 用梯度下降法來學習-Learning with gradient descent
4. 用反向傳播調整神經網絡中逐層所有神經元的超參數
5. 過擬合問題
6. IMPLEMENTING A NEURAL NETWORK FROM SCRATCH IN PYTHON – AN INTRODUCTION

 

0. 引言

0x1: 神經網絡的分層神經元意味着什么

為了解釋這個問題，我們先從一個我們熟悉的場景開始說起，電子電路的設計

如上圖所示，在實踐中，在解決線路設計問題(或者大多數其他算法問題)時，我們通常先考慮如何解決子問題，然后逐步地集成這些子問題的解。換句話說，我們通過多層的抽象來獲得最終的解答，回到上圖的電路，我們可以看到，不論多么復雜的電路功能，在最底層的底層，都是由最簡單的"與、或、非"門通過一定的邏輯關系組成

這就很自然地讓我么聯想到深度神經網絡的一張膾炙人口的架構圖

深度神經網絡中間的隱層可以理解為是一種逐層抽象封裝的思想，這么說可能並沒有嚴格的理論依據，但是卻十分符合我自己直覺上的理解，例如，如果我們在進行視覺模式識別

1. 第一層的神經元可能學會識別邊
2. 第二層的神經元可以在邊的基礎上學會識別更加復雜的形狀(例如三角形或者矩形)
3. 第三層能夠識別更加復雜的形狀
4. 以此類推，這些多層的抽象看起來能夠賦予深度網絡一種學習解決復雜模式識別問題的能力

借着這個話題，我們引申出一個很有趣的論點

用4個參數可以描繪出一個大象，如果給我5個參數，我甚至可以讓它卷鼻子

通過線性方程組來擬合一個數據集，本質是說世界上的所有的事物都可以用線性方程組來描繪

https://publications.mpi-cbg.de/Mayer_2010_4314.pdf

0x2: 神經網絡的普遍性(神經網絡可以計算任何函數)

神經網絡的一個最顯著的事實就是它可以計算任何的函數，不管目標數據集對應的函數是什么樣的，總會確保有一個神經網絡能夠對任何可能的輸入x，其值f(x)或者某個足夠准確的近似是網絡的輸出。這表明神經網絡擁有一種"普遍性"，普遍性是指，在原理上，神經網絡可以做所有的事情

1. 兩個預先聲明

在討論普遍性定理成立之前，我們先定義下兩個預定聲明，即"神經網絡可以計算任何函數"

1. 這句話不是說一個網絡可以被用來准確地計算任何函數，而是說，我們可以獲得盡可能好的一個"近似"(即擬合)，同時通過增加隱藏元的數量，我們可以提升近似的精度
2. 只要連續函數才可以被神經網絡按照上面的方式去近似

總的來說，關於普遍性定理的表述應該是: 包含一個及以上隱藏層的神經網絡可以被用來按照任意給定的精度來近似任何連續函數

2. 激活函數輸出值在各個區間的累加和抵消

這樣寫標題可能有些奇怪，但這是我個人這個現象的理解，這個情況在我們高中數學中並不少見，即每個函數都有自己的定義域和值區間，當把兩個函數相加時需要同時考慮它們的定義域區間，最終得到"累加和抵消"后的函數結果，而我們網絡中每個神經元對應的激活函數輸出值都可以看作是一個函數，我們回到我們的sigmoid S型函數，把它的w權重設置為一個較大的值，想象一下它的函數曲線會是下面這個樣子(接近階躍函數)

可以看到，S型函數的階躍點為 s = -b / w: 和b成正比，和w成反比，在這種前提下，隱藏層的加權輸出(w1a1 + w2a2)就可以近似看成是一組階躍函數的輸出，那問題就好辦了

這些事情就變得很有趣的，由於b不同，導致階躍點不同，每個神經元的激活值輸出函數的階躍點是錯開的，這就允許我們通過調整b(當然階躍點也受w的影響)來構造任意的突起。在注意第二點，這個突起的高度是誰決定的？答案也很明顯，它是由這一層的激活值輸出乘上下一層的權重的累加值決定的。以上2點達成后，我們具備了一個能力: 可以在一個隱藏層中通過有效地調整w和b，來構造任意寬、任意高的"塔形凸起"

當繼續增加神經元的組合時，我們可以構造出更復雜的塔形突起

總的來說，通過改變權重和偏置，我們實際上是在設計這個擬合函數

Relevant Link:

http://neuralnetworksanddeeplearning.com/
http://neuralnetworksanddeeplearning.com/chap4.html
https://github.com/ty4z2008/Qix/blob/master/dl.md
http://neuralnetworksanddeeplearning.com/chap1.html
http://neuralnetworksanddeeplearning.com/

 

1. 感知器及激活函數

為了更好的理解神經網絡的"決策過程"，我么需要先了解激活函數以及它的理論前身: 感知器，請注意我這里用詞，決策過程，不管是多少層的神經網絡，每一層/每一層上的每一個神經元都不不斷進行"決策"，在深度神經網絡中這通過激活函數來支持(我們稍后再詳細討論激活函數，現在只要知道激活函數為這個決策提供了輸入)

0x1: 感知器

我們剛才提到決策這個概念，一個感知器接受幾個二進制輸入x1、x2、x3...，並產生一個二進制輸出

同時，對每個二進制輸入(對應圖上左邊的3根箭頭)都定義了權重w1、w2、w3，表示相應輸入對於輸出(決策)重要性的實數

可以看到，這里就包含了一個最簡單朴素的決策器思想，並且隨着權重w和閾值threshold的變化，你可以得到不同的"決策模型"，我們把這些感知器組成一個層狀網絡

這個感知器網絡能做出一些很"微秒"的決策

1. 第一層感知器通過權衡輸入依據做出3個非常簡單的決定
2. 第二層感知器可以比第一層做出更復雜和抽象的決策
3. 第三層中的感知器甚至能進行更復雜的決策
4. 以這種方式，一個多層的感知器網絡可以從事復雜巧妙的決策

再觀察一個細節，每一層的感知器都和上一層的所有感知器的輸入進行了"全連接"，這意味着從第二層開始每一個層的所有感知器都是一個獨立的決策者。

我們把每一層的權重累加改寫為，這里的w和x對應權重和輸入的向量，然后把閾值threshold移到不等式的另一邊，並用b = -threshold代替，用偏置而不是閾值，那么感知器的決策規則可以重寫為

我么可以把偏置看作一種表示讓感知器輸出1(或者用生物學的術語即"激活感知器")，即輸入和權重和乘積累加加上這個偏置到達甚至超過這個感知器的"激活點"，讓它達到"激活態"

0x2: S型神經元(sigmoid激活函數)

感知器很好，它體現了一個多路輸入綜合決策的思想，但是我們仔細看一下感知器的函數圖，它是一個階躍函數，它最大的一個問題就是階躍點附近會產生巨大的翻轉，體現在感知器網絡上就是單個感知器的權限或者偏置的微小改動有時候會引起那個感知器的輸出的完全翻轉。這也很容易想象，因為在階躍點附近，感知器的輸出是瞬間從0->1或者1->0的，這本質是感知輸入決策是一種階躍函數，它不具備函數連續性，不具備連續性的函數自然也無法對輸入的微小改變做出相應的微小改變

為了解決非連續性的問題，我么可以引入一個稱為S型神經元的人工神經元，S型神經元最大的特點就是輸入權重和偏置的微小改動只會引入輸出的微小變化，這對讓神經網絡學習起來是很關鍵的

上面被稱為S型函數，這實際上也就是sigmoid激活函數的單個形式，權重和輸入的乘積累加，和偏置的和的輸出是

可以看到，S型函數是一個連續函數

這個函數可以看成是感知器階躍函數平滑后的版本，Sigmoid激活函數的平滑意味着權重和偏置的微小變化，會從神經元產生一個微小的輸出變化

0x3: tanh激活函數(雙曲正切  hyperbolic tangent函數)

除了S型激活函數之外，還有很多其他類型的激活函數，tanch函數的輸入為，，通過簡單的代數運算，我們可以得到: 。可以看出，tanh是S型函數的按比例變化版本

tanh在特征相差明顯時的效果會很好，在循環過程中會不斷擴大特征效果。與 sigmoid 的區別是，tanh 是 0 均值的，因此實際應用中 tanh 會比 sigmoid 更好

0x4: ReLu激活函數(修正線性神經元 rectified linear neuron)

輸入為x，權重向量為w，偏置為b的ReLU神經元的輸出是: ，函數的形態是這樣的

ReLU 得到的 SGD 的收斂速度會比 sigmoid/tanh 快很多，因為它不存在在"在接近0或1時學習速率大幅下降"的問題

0x5: softmax激活函數(柔性最大值)

softmax 的想法其實就是為神經網絡定義一種新式的輸出層。開始時和 sigmoid 層一樣的，首先計算帶權輸入: ，不過，這里我們不會使用 sigmoid 函數來獲得輸出。而是，會應用一種叫做 softmax 函數

分母是對所有的輸出神經元進行求和。該方程同樣保證輸出激活值都是正數，因為指數函數是正的。將這兩點結合起來，我們看到 softmax 層的輸出是一些相加為 1 正數的集合。換言之，softmax 層的輸出可以被看做是一個概率分布。這樣的效果很令人滿意。在很多問題中，將這些激活值作為網絡對於某個輸出正確的概率的估計非常方便。所以，比如在 MNIST 分類問題中，我們可以將 輸出值解釋成網絡估計正確數字分類為 j 的概率

Relevant Link:

http://www.jianshu.com/p/22d9720dbf1a 

 

2. 代價函數(loss function)

我們已經了解了組成神經網絡的基本單元S型神經單元，並且了解了它的基本組成架構

現在我們將注意力從單個神經元擴展到整個網絡整體，從整體的角度來看待所有神經元對最后輸入"最終決策"的影響，網絡中每一層的所有的權重和偏置在輸入的作用下，最終在輸出層得到一個輸出向量，這個時候問題來了，網絡預測的輸出結果和我們預期的結果(label)一致嗎？它們差距了多少？以及是哪一層的哪一個神經元(或者多個神經元)的參數沒調整好導致了這種偏差(這個問題在之后的梯度下降會詳細解釋)，為了量化這些偏差，我們需要為神經網絡定義一個代價函數，代價函數有很多形式

下面只會簡單的介紹並給出對應代價函數的數學表示，而不是詳細討論，因為代價函數本身沒啥可以討論的，它的真正用途在於對各層神經元的w/b進行偏微分求導，從而得到該如何調整修正各個神經元w/b的最優化指導，這是一種被稱為梯度下降的技術

0x1: 二次代價函數(均方誤差 MSE)

y(x) - a是目標值和實際輸出值的差，可以看到，當對於所有的訓練輸入x，y(x)都接近於輸出a時(即都預測正確時)，代價函數C(w, b)的值相當小，換句話說，如果我們的學習算法能找到合適的權重和偏置，使得C(w, b) = 0，則該網絡就是一個很好的網絡，因此這就表明，我們訓練的目的，是最小化權重和偏置的代價函數，我們后面會說道將使用梯度下降來達到這個目的

1. 神經元飽和問題(僅限S型神經元這類激活函數)

在開始探討這個問題前，先來解釋下什么是神經元飽和，當然這里依然需要下面將要講到的梯度下降的相關知識

1. 我們知道，循環迭代訓練神經網絡的根本目的是尋找到一組w和b的向量，讓當前網絡能盡量准確地近似我們的目標數據集
2. 而要達到這個目的，其中最關鍵的一個"反饋"，最后一層輸出層的結果和目標值能夠計算出一個代價函數，根據這個代價函數對權重和偏置計算偏微分(求導)，得到一個最佳下降方向
3. 知道第二步之前都沒問題，問題在於"二次代價函數+Sigmoid激活函數"的組合，得到的偏導數和激活函數本身的導致有關，這樣，激活函數的曲線緩急就直接影響了代價函數偏導數的緩急，這樣是很不高效的，常常會遇到"神經元飽和"問題，即如果一個S型神經元的值接近1或者0，它認為自己已經接近優化完畢了，它會降低自己的激活導致，讓自己的w和b趨於穩定，但是如果恰好這個w和b是隨機初始的錯誤值或者不小心進入了一個錯誤的調整，則很難再糾正這個錯誤，有點撞了南牆不回頭的意思

這么說可能會很抽象，我們通過數學公式推導和可視化函數圖像來說明這點，首先，我們的二次代價函數方程如下

我們有，其中。使用鏈式法則來求權重和偏置的偏導數有

我們發現，公式中包含了這一項，仔細回憶下的函數圖像

從這幅圖可以看出，當神經元的輸出接近1的時候(或者0)，曲線變得相當平，所以就很小了，帶回上面的方程，則w和b的偏導數方程也就很小了，這就導致了神經元飽和時學習速率緩慢的原因。如果正確調整了倒還好，如果是因為初始化或者錯誤的調整導致進入了一個錯誤的方向，則要調整回來就變得很緩慢很困難

對着這個這題，我們再延伸出去思考一下，導致學習速率緩慢的罪魁禍首是S型神經元的這種曲線特性導致的是吧？那如果不用S型呢，用ReLU呢，是不是就不存在這種情況呢？答案是肯定的，至少不存在學習速率緩慢的問題(雖然ReLU也有自己的缺點)

所以嚴格來說，並不是二次代價函數MSE導致的神經元飽和，是二次代價函數和S型的組合存在神經元飽和的問題

2. 輸出層使用線性神經元時使用二次代價函數不存在學習速率慢的問題

如果我們輸出層的神經元都是線性神經元，而不再是S型函數的話，即使我么繼續使用二次代價函數，最終關於權重和偏置的偏導數為

這表明如果輸出神經元是線性的那么二次代價函數不再會導致學習速率下降的問題，在此情形下，二次代價函數就是一種合適的選擇

0x2: 交叉熵代價函數

有句話說得好: "失敗是成功之母"，如果我們能及時定義自己犯得錯誤並及時改正，那么我們的學習速度會變得很快，同樣的道理也適用在神經網絡中，我們希望神經網絡可以從錯誤中快速地學習。我們定義如下的代價函數

通過數學分析我們同樣可以看出

1. C > 0: 非負
2. 在實際輸出和目標輸出之間的差距越小，最終的交叉熵的值就越低

這其實就是我們想要的代價函數的特性

1. 交叉熵代價函數解決神經元飽和問題

同時它也避免了學習速度下降的問題，我們來看看它的偏導數情況，我們將代入前式的鏈式偏導數中

這個公式很有趣也很優美，它告訴我們權重學習的速度受到，也就是輸出中的誤差的控制，更大的誤差，更快的學習速率，這是一種非常符合我們直覺認識的一種現象，類似的，我們也可以計算出關於偏置的偏導數

這正是我們期待的當神經元開始出現嚴重錯誤時能以最快速度學習。事實上，如果在輸出神經元是S型神經元時，交叉熵一般都是更好的選擇

2. 交叉熵究竟表示什么

交叉熵是一種源自信息論的解釋，它是"不確定性"的一種度量，交叉熵衡量我們學習到目標值y的正確值的平均起來的不確定性

1. 如果輸出我們期望的結果，不確定性就會小一些
2. 反之，不確定性就會大一些 

0x3: multiclass svm loss(hinge loss)

http://vision.stanford.edu/teaching/cs231n-demos/linear-classify/

Relevant Link:

https://hit-scir.gitbooks.io/neural-networks-and-deep-learning-zh_cn/content/chap3/c3s1.html

 

3. 用梯度下降法來學習-Learning with gradient descent

在上面討論清楚了代價函數的相關概念之后，我們接下來可以毫無障礙地繼續討論梯度下降的這個知識了。我們再次重申一下我們的目標，我們需要不斷調整w和b向量組，找到一組最佳的向量組，使之最終計算得到的代價函數C最小(C最小也就意味着最大化的擬合)

我們先從一個最簡單的情況切入話題，我們設計一個神經網絡，它只有一個輸入、一個輸出，權重w = 1，偏置b = 2，代價函數為 C = || (a - y) ||

我們的輸入x  = 1，可以看到，神經元輸出的值為3，代價函數為3，我們的目標是讓C降為0(x是不變的)，為此我們需要調整w和b的值，當讓這個例子太簡單了，我們知道怎么做，但是如果這里的神經元有多個呢，層數有多層呢，更重要的是，我們需要讓計算機自動完成這個過程。為此回答這個問題，我們需要引入梯度這個概念

1. 我們需要根據這里的代價函數計算出對w和b的偏導數，這里都是-1
2. 引入一個學習速率的概念，它表示一個學習調整的步長，設置為1
3. 接着我們每次把w和b分別進行: w = w - 1 * -1，b = b - 1 * -1
4. 很容易想象，在進行了2次學習后，此時w = -1，b = 1，此時代價函數C = 0，學習完成

這里根據代價函數C求權重和偏置的偏導數，並根據學習速率，逐輪調整w和b的思想，就是梯度下降。同樣的問題推廣到二次函數也是類似的

0x1: 使用梯度下降來尋找C的全局最小點

再次重申，我們訓練神經網絡的目的是找到能最小化二次代價函數C(w, b)的權重和偏置，拋開所有細節不談，現在讓我們想象我們只要最小化一個給定的多元函數(各個神經元上的w和b就是它的變元): C(v)，它可以是任意的多元實值函數，想象C是一個只有兩個變量v1和v2的函數

我們想要找到C的全局最小值，一種解決這個問題的方式是用微積分來解析最小值，我們可以計算導數(甚至二階導數)去尋找C的極值點，這里引入一個額外的話題: 隨機梯度下降(SGD)

1. 對於一次訓練來說，輸入的x是固定值，代表了所有樣本的輸入值
2. 梯度下降要做的是計算所有輸入值的"累加平均梯度"(這里會有一個累加符號)，並根據最終總的累加平均梯度來反饋到各層的w和b上，讓其作出相應調整
3. 問題就來了，當輸入樣本量十分巨大的時候，計算所有這些累加平均梯度是一件十分耗時的工作，所以為了改進這個問題，使用了隨機mini_batch技術，即從這批樣本中隨機選出一定數目的樣本作為代表，代表這批樣本進行計算累加平均梯度，計算得到的梯度再反饋給所有整體樣本，用這種方式提高運算效率
4. 假設我么總共樣本是100，我們選的mini-batch = 10，則我們每次隨機選取10個樣本計算梯度，然后繼續重復10次，把所有樣本都輪一邊(當然隨機抽樣不能保證一定所有樣本都覆蓋到)，這被稱為完成了一個"訓練迭代(epoch)"

我們把我們的代價函數C想象成一個山谷，我們當前的w/b想象成在山谷中的某個點，我們的梯度下降就是當前小球沿重力作用要滾落的方向，學習率可以看成是速度v，而每次w/b調整的的大小可以看成是位移

微積分告訴我們C將會有如下變化: ，進一步重寫為: 。這個表達式解釋了為什么被稱為梯度向量，因為它把v的變化關聯為C的變化，整個方程讓我們看到了如何選取才能讓C下降: ，這里的是個很小的正數(稱為學習速率)。至此，C的變量的變化形式我們得到了: 。然后我們用它再次更新規則計算下一次移動，如果我們反復持續這樣做，我們將持續減小C直到獲得一個全局最小值。總結一下

梯度下降算法工作的方式就是重復計算梯度然后沿着相反的方向移動，沿着山谷"滾落"

從舉例中回到權重w和偏置的情況也是一樣的，我們用w和b代替變量v

0x2: 基於momentum的梯度下降

為了理解momentum技術，想想我么關於梯度下降的原始圖片，其中我們研究了一個球滾向山谷的場景，我們稱之為梯度下降，momentum技術修改了梯度下降的兩處使之更加貼近於真實物理場景

1. 為我們想要優化的參數引入了一個稱為速度(velocity)的概念，梯度的作用就是改變速度(物理中力的作用是改變速度，而不是位移)
2. momentum方法引入了一種摩擦力的項，用來逐步減少速度

我們將梯度下降更新規則: 改為

我們來仔細看一看上面這個方程，它真正變化的量是v，每一輪計算新的v之前都要乘上一個因子u，然后減去學習率乘以代價函數差值(這個和普通梯度是一樣的)，唯一的區別就在那個因子u

在上面方程中是用來控制阻礙或者摩擦力的量的超參數，為了理解這個參數的意義，我么可以考慮一下

1. u = 1的時候，對應於沒有任何摩擦力，此時我們看到代價函數差值直接改變速度v，速度v隨后再控制w的變化率。直覺上想象一下，我們朝着梯度的方向不斷下降，由於v的關系，當我們到達谷底的時候，還會繼續越過去，這個時候如果梯度本該快速改變而沒有改變，我們會發現我們在錯誤的方向上移動太多了，雖然此時代價函數已經翻轉了，但是不能完全抵消v的影響
2. 前面提到，u可以控制系統中摩擦力的大小，更加准確的說，我們應該將"1 - u"看作是摩擦力的量
　　1) 當u = 1沒有摩擦，速度完全由梯度導數決定
　　2) 當u = 0就存在很大摩擦，速度無法疊加，上訴公式就退化成了普通的梯度下降公式

0x3: rmsprop

SGD的問題在於如果我們把learning rate設置的很小，則SGD會花費一個相當長的過程，為此，我們有很多對SGD的改進梯度下降方法，接下來逐一研究

The basic idea behind rmsprop is to adjust the learning rate per-parameteraccording to the a (smoothed) sum of the previous gradients. Intuitively this means that

1. frequently occurring features get a smaller learning rate (because the sum of their gradients is larger): 梯度越大，一次參數調整的size就要越小，這相當於速度很快了，時間s就要動態調整小，防止一次移動的距離s過大(步子邁的太大扯着蛋)
2. and rare features get a larger learning rate: 梯度越小，一個參數調整的size就要越大

The implementation of rmsprop is quite simple. For each parameter we keep a cache variable and during gradient descent we update the parameter and the cache as follows (example for ):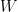

cacheW = decay * cacheW + (1 - decay) * dW ** 2
W = W - learning_rate * dW / np.sqrt(cacheW + 1e-6)

The decay is typically set to 0.9 or 0.95 and the 1e-6 term is added to avoid division by 0.

可以看到，RMSPROP的做法和momentum的梯度下降核心思想是一樣的，這是一種對不同的梯度進行動態補償調整的機制，目的是讓網絡在大梯度情況下慢慢收斂，而在平緩梯度的時候盡快前進

0x4: (Nesterov) Momentum Method

0x5: AdaGrad

AdaGrad是RMSPROP的"old version"，RMSPROP是在AdaGrad的基礎上改進而來的，我們來看看AdaGrad的定義

historical_grad += g^2
adjusted_grad = grad / (fudge_factor + sqrt(historical_grad))
w = w - master_stepsize*adjusted_grad

缺點是因為公式中分母上會累加梯度平方，這樣在訓練中持續增大的話，會使學習率非常小，甚至趨近無窮小

0x6: AdaDelta

0x7: Adam

Adam可以理解為momutum SGD和RMSPROP的綜合改進版本，同時引入了動態調整特性以及動量V特性。Adam(Adaptive Moment Estimation)本質上是帶有動量項的RMSprop，它利用梯度的一階矩估計和二階矩估計動態調整每個參數的學習率。Adam的優點主要在於經過偏置校正后，每一次迭代學習率都有個確定范圍，使得參數比較平穩。公式如下

Relevant Link:

http://www.wildml.com/2015/09/implementing-a-neural-network-from-scratch/
http://blog.csdn.net/yc461515457/article/details/50498266
https://tigerneil.gitbooks.io/neural-networks-and-deep-learning-zh/content/chapter3b.html
http://blog.csdn.net/u012759136/article/details/52302426

 

4. 用反向傳播調整神經網絡中逐層所有神經元的超參數 

這個話題是針對整個神經網絡的所有神經元而言的，是一個整體優化的話題，在開始討論這個話題前，我們先看一張多層神經網絡的架構圖

我們設想一下，我們在當前超參數的前提下，根據一組輸入值x，得到了一個代價函數，接下來我們要怎么把這種誤差傳遞給每一層的所有神經元呢，答案就是對所有神經元反向計算梯度，即要對每一層每一個神經元的w/b計算偏導數

這張圖實際上為了說明接下來要討論的"消失的梯度"的問題的，但是我認為它同樣表達出了反向傳播的核心思想，仔細看這個方程，我們會發現幾點

1. 越前面層的神經元相對於C的偏導數，可以通過后面層的神經元的偏導數推演而得，直觀上就像從最后一層反向傳播到了第一層一樣，故名反向傳播
2. C對逐層神經元的w/b的偏導數，隨着越往前，偏導數乘的因子越多

0x2: 反向傳播算法標准化流程

仔細看這個算法，我么可以看到為何它被稱為反向傳播，我們從最后一層開始向后計算誤差向量，這種反向移動其實是代價函數是網絡輸出的函數的結果。說動這里引入一個題外話

1. 前饋網絡: 輸入x通過一層一層的w/b逐步把影響傳遞到最后一層輸出層
2. 反向傳播: 這個時候輸入可以看作是代價函數C，通過鏈式求導反向逐層把C的誤差值傳遞給前面每一層的每一個神經元

這2點讓我影響深刻，充滿了哲學思想

0x3: 不穩定的梯度問題(梯度激增/消失)

我們從一個現象引出這個話題: 多層神經網絡並不能顯著提高整體的精確度，在一個網絡框架的基礎上，再增加新的一層神經元，網絡的整體精確度並沒有顯著提升？這是為什么呢？新增加的隱層沒有增加網絡對抽象問題的決策能力嗎？

我們來看一個多層神經網絡各個層的學習速率的變化曲線對比圖

我們可以發現，每層的神經元的學習速率都差了一個數量級，越前面層的神經元，獲得的學習速率越小，這種現象也被稱為"消失的梯度(vanishing gradient problem)"，同時值得注意的是，這種情況也存在反例，即前面層的神經元學習速率比后面的大，即"激增的梯度問題(exploiding gradient problem)"。更一般的說，在深度神經網絡中的梯度是不穩定的，在前面的層中會消失或激增

這種現象背后的數學原理是啥呢？我么再次來看一下前面那張代價函數對各層神經元的偏導數

我們知道，越前面的神經元，代價函數C對w/b的偏導數的公式中，乘積因子越多，所以接下來問題就是這些多出來的乘積因子對結果產生什么影響了呢？為了理解每個項的行為，先看看下面的sigmoid函數導數的圖像

該導數在時達到最高值。現在，如果我們使用標准方法來初始化網絡中的權重，那么會使用一個均值為0標准差為1的高斯分布，因此所有的權重會滿足 |wj|<1。有了這些信息，我們發現會有 wjσ′(zj)<1/4。並且在我們進行了所有這些項的乘積時，最終結果肯定會指數級下降：項越多，乘積的下降的越快。這就是消失的梯度問題的合理解釋。

Relevant Link:

https://tigerneil.gitbooks.io/neural-networks-and-deep-learning-zh/content/chapter5.html
http://blog.csdn.net/yc461515457/article/details/50499515

 

5. 過擬合問題

在科學領域有一種說法，一個擁有大量參數的模型能夠描述特別神奇的現象，但即使這樣的模型能夠很好地擬合已有的數據，但並不表示它就是一個好的模型，因為這可能只是模型中足夠的自由度使得它可以描述幾乎所有給定大小的數據集，而不需要真正洞察現象背后的本質。所以發生這種情形時，模型對已有的數據會表現的很好，但是對新的數據很難泛化。事實上，對一個模型真正的檢驗就是它對沒有見過的場景的"預測能力"

0x1: 過擬合(overfitting)/過度訓練(overtrainning)在神經網絡訓練中表現出的幾種現象

1. 訓練集和測試集的准確率曲線沒有一致收斂

網絡幾乎是在單純記憶訓練集合，而沒有對數字本質進行理解能夠泛化到測試數據集上

2. 訓練數據集准確度曲線在到達一定迭代次數后維持在一個數值周圍上線劇烈浮動

0x2: 如何規避過擬合問題

1. 在train_set/test_set的基礎上，增加validate_set驗證數據集判斷是否需要提前停止

我們使用validate_set來防止過度擬合，在每個迭代周期的最后都計算在validate_set上的分類准確度，一旦分類准確度已經飽和，就停止訓練，這個策略被稱為"提前停止"

在網絡根據訓練數據集進行訓練的過程中，我們借助validate_set來不斷驗證各種超參數，然后一旦獲得了想要的超參數，最終我們就使用test_set進行准確率測量，這給了我們在test_set上的結果是一個網絡泛化能力真正的度量。換言之，你可以將驗證集看成一種特殊的訓練數據集能夠幫助我們學習好的超參數。這種尋找好的超參數的方法有時被稱為"hold out"方法(因為validate_set是從training_set中留出或者拿出一部分)

2. 增加訓練樣本的數量

思考一個最簡單的問題，我們有1000個超參數，但是訓練樣本只有100個，那么平均下來就是10個超參數去擬合一個樣本，這給參數擬合帶來了很大的自由度，也就很容易造成過擬合。一般來說，最好的降低過擬合度的方式之一就是增加訓練樣本的量。有了足夠的訓練數據，就算是一個規模非常大的網絡也不大容易過度擬合

3. 規范化

規范化能夠幫助我們解決過度擬合的問題，規范化有很多種方式，例如L1規范化、L2規范化，本小節我們重點討論L2規范化，他在實際的Tensorflow或者thoeno中用的最多

L2規范化，也叫權重衰減(weight decay)，它的思想是增加一個額外的項到代價函數上，這個項叫做規范化項，下面就是規范化的交叉熵

注意到第二個項是新加入的所有權重的平方的和。然后使用一個因子 λ/2n 進行量化調整，其中 λ>0 可以成為 規范化參數，而 n 就是訓練集合的大小。當然，對其他的代價函數也可以進行規范化，例如二次代價函數。類似的規范化的形式如下

兩者都可以寫成這樣

直覺上看，規范化的效果是讓網絡傾向於學習小一點的權重，換言之，規范化可以當作一種尋找小的權重和最小化原始代價函數之間的折中，這兩部分之前相對的重要性就由 λ 的值來控制了：λ 越小，就偏向於最小化原始代價函數，反之，傾向於小的權重。

思考一個問題，為什么規范化能夠幫助減輕過度擬合？我們要明白，規范化只是一種術語說法，它的本質是通過改變原始代價函數的方程式，讓代價函數有的新的屬性，即誘導網絡學習盡量小的權重，這背后的道理可以這么理解:

小的權重在某種程度上，意味着更低的復雜性，也就對數據給出了一種更簡單卻更強大的解釋，因此應該優先選擇

讓我們從抗噪音干擾的角度來思考這個問題，假設神經網絡的大多數參數有很小的權重，這最可能出現在規范化的網絡中。更小的權重意味着網絡的行為不會因為我們隨便改變一個輸入而改變太大。這會讓規范化網絡學習局部噪聲的影響更加困難。將它看作是一種讓單個的證據不會影響整個網絡輸出太多的方式。相對的，規范化網絡學習去對整個訓練集中經常出現的證據進行反應，對比看，大權重的網絡可能會因為輸入的微小改變而產生比較大的行為改變

4. 棄權(Dropout)技術

棄權是一種相當激進的技術，和L1/L2規范化不同，棄權技術並不依賴對代價函數的修改，而是在棄權中，我們改變了網絡本身，假設我們嘗試訓練一個網絡

特別地，假設我們有一個訓練數據 x 和 對應的目標輸出 y。通常我們會通過在網絡中前向傳播 x ，然后進行反向傳播來確定對梯度的共現。使用 dropout，這個過程就改了。我們會從隨機（臨時）地刪除網絡中的一半的神經元開始，讓輸入層和輸出層的神經元保持不變。在此之后，我們會得到最終的網絡。注意那些被 dropout 的神經元，即那些臨時性刪除的神經元，用虛圈表示在途中

我們前向傳播輸入，通過修改后的網絡，然后反向傳播結果，同樣通過這個修改后的網絡。在 minibatch 的若干樣本上進行這些步驟后，我們對那些權重和偏差進行更新。然后重復這個過程，首先重置 dropout 的神經元，然后選擇新的隨機隱藏元的子集進行刪除，估計對一個不同的minibatch的梯度，然后更新權重和偏差

為了解釋所發生的事，我希望你停下來想一下沒有 dropout 的訓練方式。特別地，想象一下我們訓練幾個不同的神經網絡，使用的同一個訓練數據。當然，網絡可能不是從同一初始狀態開始的，最終的結果也會有一些差異。出現這種情況時，我們可以使用一些平均或者投票的方式來確定接受哪個輸出。例如，如果我們訓練了五個網絡，其中三個被分類當做是 3，那很可能它就是 3。另外兩個可能就犯了錯誤。這種平均的方式通常是一種強大（盡管代價昂貴）的方式來減輕過匹配。原因在於不同的網絡可能會以不同的方式過匹配，平均法可能會幫助我們消除那樣的過匹配。

那么這和 dropout 有什么關系呢？啟發式地看，當我們丟掉不同的神經元集合時，有點像我們在訓練不同的神經網絡。所以，dropout 過程就如同大量不同網絡的效果的平均那樣。不同的網絡以不同的方式過匹配了，所以，dropout 的網絡會減輕過匹配。

一個相關的啟發式解釋在早期使用這項技術的論文中曾經給出

因為神經元不能依賴其他神經元特定的存在，這個技術其實減少了復雜的互適應的神經元。所以，強制要學習那些在神經元的不同隨機子集中更加健壯的特征

換言之，如果我們就愛那個神經網絡看做一個進行預測的模型的話，我們就可以將 dropout 看做是一種確保模型對於證據丟失健壯的方式。這樣看來，dropout 和 L1、L2 規范化也是有相似之處的，這也傾向於更小的權重，最后讓網絡對丟失個體連接的場景更加健壯

5. 人為擴展訓練數據

我們前面說過，減少過擬合的一個最好的手段就是增加訓練樣本量，但這在很多場景是很難做到的，在圖像識別領域，為了彌補樣本量不夠的問題，人們想出了一種擴大訓練樣本量的方法，即數據擴展，例如

1. 圖像翻轉
2. 圖像平移
3. 模擬人手肌肉的圖像線條抖動
..

Relevant Link:

https://tigerneil.gitbooks.io/neural-networks-and-deep-learning-zh/content/chapter3a.html

 

6. IMPLEMENTING A NEURAL NETWORK FROM SCRATCH IN PYTHON – AN INTRODUCTION

0x1: LOGISTIC REGRESSION(使用邏輯回歸分類器分類兩類圓環點集)

import numpy as np
from sklearn import datasets, linear_model
import matplotlib.pyplot as plt


def generate_data():
    np.random.seed(0)
    X, y = datasets.make_moons(200, noise=0.20)
    return X, y


def visualize(X, y, clf):
    # plt.scatter(X[:, 0], X[:, 1], s=40, c=y, cmap=plt.cm.Spectral)
    # plt.show()
    plot_decision_boundary(lambda x: clf.predict(x), X, y)
    plt.title("Logistic Regression")


def plot_decision_boundary(pred_func, X, y):
    # Set min and max values and give it some padding
    x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
    y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
    h = 0.01
    # Generate a grid of points with distance h between them
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # Predict the function value for the whole gid
    Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    # Plot the contour and training examples
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Spectral)
    plt.show()


def classify(X, y):
    clf = linear_model.LogisticRegressionCV()
    clf.fit(X, y)
    return clf


def main():
    X, y = generate_data()
    # visualize(X, y)
    clf = classify(X, y)
    visualize(X, y, clf)


if __name__ == "__main__":
    main()

可以看到，邏輯回歸盡可能地忽略噪音(從直線擬合的角度看的噪音)，用一條直線對數據集進行了分類，但是很明顯，邏輯回歸沒有"理解"數據背后真正的"含義"，沒有把圓環給分類出來

0x2: TRAINING A NEURAL NETWORK

Let’s now build a 3-layer neural network with one input layer, one hidden layer, and one output layer. The number of nodes in the input layer is determined by the dimensionality of our data, 2. Similarly, the number of nodes in the output layer is determined by the number of classes we have, also 2. (Because we only have 2 classes we could actually get away with only one output node predicting 0 or 1, but having 2 makes it easier to extend the network to more classes later on). The input to the network will be x- and y- coordinates and its output will be two probabilities, one for class 0 (“female”) and one for class 1 (“male”). It looks something like this:

1. HOW OUR NETWORK MAKES PREDICTIONS

Our network makes predictions using forward propagation, which is just a bunch of matrix multiplications and the application of the activation function(s) we defined above. If x is the 2-dimensional input to our network then we calculate our prediction 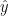 (also two-dimensional) as follows:

2. LEARNING THE PARAMETERS

Learning the parameters for our network means finding parameters () that minimize the error on our training data. But how do we define the error? We call the function that measures our error the loss function. A common choice with the softmax output is the categorical cross-entropy loss (also known as negative log likelihood). If we have 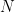 training examples and  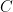classes then the loss for our prediction  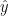with respect to the true labels  is given by:

We can use gradient descent to find the minimum and I will implement the most vanilla version of gradient descent, also called batch gradient descent with a fixed learning rate. Variations such as SGD (stochastic gradient descent) or minibatch gradient descent typically perform better in practice. So if you are serious you’ll want to use one of these, and ideally you would also decay the learning rate over time.

3. IMPLEMENTATION

import numpy as np
from sklearn import datasets, linear_model
import matplotlib.pyplot as plt


class Config:
    nn_input_dim = 2  # input layer dimensionality
    nn_output_dim = 2  # output layer dimensionality
    # Gradient descent parameters (I picked these by hand)
    epsilon = 0.01  # learning rate for gradient descent
    reg_lambda = 0.01  # regularization strength


def generate_data():
    np.random.seed(0)
    X, y = datasets.make_moons(200, noise=0.20)
    return X, y


def visualize(X, y, model):
    # plt.scatter(X[:, 0], X[:, 1], s=40, c=y, cmap=plt.cm.Spectral)
    # plt.show()
    plot_decision_boundary(lambda x:predict(model,x), X, y)
    plt.title("Logistic Regression")


def plot_decision_boundary(pred_func, X, y):
    # Set min and max values and give it some padding
    x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
    y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
    h = 0.01
    # Generate a grid of points with distance h between them
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # Predict the function value for the whole gid
    Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    # Plot the contour and training examples
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Spectral)
    plt.show()


# Helper function to evaluate the total loss on the dataset
def calculate_loss(model, X, y):
    num_examples = len(X)  # training set size
    W1, b1, W2, b2 = model['W1'], model['b1'], model['W2'], model['b2']
    # Forward propagation to calculate our predictions
    z1 = X.dot(W1) + b1
    a1 = np.tanh(z1)
    z2 = a1.dot(W2) + b2
    exp_scores = np.exp(z2)
    # 得到實際預測值，用於和目標值計算代價函數
    probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
    # Calculating the loss(交叉熵)
    corect_logprobs = -np.log(probs[range(num_examples), y])
    # 針對每一個輸入樣本都要計算一個代價函數，C = 總的代價累加結果的平均值
    data_loss = np.sum(corect_logprobs)
    # Add regulatization term to loss (optional)
    data_loss += Config.reg_lambda / 2 * (np.sum(np.square(W1)) + np.sum(np.square(W2)))
    # 除以樣本數，得到平均代價函數值
    return 1. / num_examples * data_loss


def predict(model, x):
    W1, b1, W2, b2 = model['W1'], model['b1'], model['W2'], model['b2']
    # Forward propagation
    z1 = x.dot(W1) + b1
    a1 = np.tanh(z1)
    z2 = a1.dot(W2) + b2
    exp_scores = np.exp(z2)
    # 根據當前網絡的w/b向量組，根據激活函數softmax得到一組預測值輸出向量
    probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
    # 因為softmax輸出中各項和為1，所以其中值最大的那個代表了該網絡的預測項
    return np.argmax(probs, axis=1)


# This function learns parameters for the neural network and returns the model.
# - nn_hdim: Number of nodes in the hidden layer
# - num_passes: Number of passes through the training data for gradient descent
# - print_loss: If True, print the loss every 1000 iterations
def build_model(X, y, nn_hdim, num_passes=20000, print_loss=False):
    # Initialize the parameters to random values. We need to learn these.
    num_examples = len(X)
    np.random.seed(0)
    W1 = np.random.randn(Config.nn_input_dim, nn_hdim) / np.sqrt(Config.nn_input_dim)
    b1 = np.zeros((1, nn_hdim))
    W2 = np.random.randn(nn_hdim, Config.nn_output_dim) / np.sqrt(nn_hdim)
    b2 = np.zeros((1, Config.nn_output_dim))

    # This is what we return at the end
    model = {}

    # Gradient descent. For each batch...
    for i in range(0, num_passes):

        # Forward propagation
        z1 = X.dot(W1) + b1
        a1 = np.tanh(z1)
        z2 = a1.dot(W2) + b2
        exp_scores = np.exp(z2)
        # 計算softmax
        probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)

        # Backpropagation
        delta3 = probs
        delta3[range(num_examples), y] -= 1
        dW2 = (a1.T).dot(delta3)
        db2 = np.sum(delta3, axis=0, keepdims=True)
        delta2 = delta3.dot(W2.T) * (1 - np.power(a1, 2))
        dW1 = np.dot(X.T, delta2)
        db1 = np.sum(delta2, axis=0)

        # Add regularization terms (b1 and b2 don't have regularization terms)
        dW2 += Config.reg_lambda * W2
        dW1 += Config.reg_lambda * W1

        # Gradient descent parameter update
        W1 += -Config.epsilon * dW1
        b1 += -Config.epsilon * db1
        W2 += -Config.epsilon * dW2
        b2 += -Config.epsilon * db2

        # Assign new parameters to the model
        model = {'W1': W1, 'b1': b1, 'W2': W2, 'b2': b2}

        # Optionally print the loss.
        # This is expensive because it uses the whole dataset, so we don't want to do it too often.
        if print_loss and i % 1000 == 0:
            print("Loss after iteration %i: %f" % (i, calculate_loss(model, X, y)))

    return model


def classify(X, y):
    # clf = linear_model.LogisticRegressionCV()
    # clf.fit(X, y)
    # return clf

    pass


def main():
    X, y = generate_data()
    model = build_model(X, y, 3, print_loss=True)
    visualize(X, y, model)


if __name__ == "__main__":
    main()

Relevant Link:

http://www.wildml.com/2015/09/implementing-a-neural-network-from-scratch/
https://github.com/dennybritz/nn-from-scratch

Copyright (c) 2017 LittleHann All rights reserved