碼上快樂

相關內容    簡體    繁體

beta分布

本文轉載自   查看原文   2017-03-21 13:06   2562    統計學

beta分布介紹

相信大家學過統計學的都對 正態分布 二項分布 均勻分布 等等很熟悉了，但是卻鮮少有人去介紹beta分布的。

用一句話來說，beta分布可以看作一個概率的概率分布，當你不知道一個東西的具體概率是多少時，它可以給出了所有概率出現的可能性大小。

舉一個簡單的例子，熟悉棒球運動的都知道有一個指標就是棒球擊球率(batting average)，就是用一個運動員擊中的球數除以擊球的總數，我們一般認為0.266是正常水平的擊球率，而如果擊球率高達0.3就被認為是非常優秀的。

現在有一個棒球運動員，我們希望能夠預測他在這一賽季中的棒球擊球率是多少。你可能就會直接計算棒球擊球率，用擊中的數除以擊球數，但是如果這個棒球運動員只打了一次，而且還命中了，那么他就擊球率就是100%了，這顯然是不合理的，因為根據棒球的歷史信息，我們知道這個擊球率應該是0.215到0.36之間才對啊。

對於這個問題，我們可以用一個二項分布表示（一系列成功或失敗），一個最好的方法來表示這些經驗（在統計中稱為先驗信息）就是用beta分布，這表示在我們沒有看到這個運動員打球之前，我們就有了一個大概的范圍。beta分布的定義域是(0,1)這就跟概率的范圍是一樣的。

接下來我們將這些先驗信息轉換為beta分布的參數，我們知道一個擊球率應該是平均0.27左右，而他的范圍是0.21到0.35，那么根據這個信息，我們可以取α=81,β=219


之所以取這兩個參數是因為：

  • beta分布的均值是\frac{\alpha}{\alpha+\beta}=\frac{81}{81+219}=0.27
  • 從圖中可以看到這個分布主要落在了(0.2,0.35)間，這是從經驗中得出的合理的范圍。

在這個例子里，我們的x軸就表示各個擊球率的取值，x對應的y值就是這個擊球率所對應的概率。也就是說beta分布可以看作一個概率的概率分布。

那么有了先驗信息后，現在我們考慮一個運動員只打一次球，那么他現在的數據就是”1中;1擊”。這時候我們就可以更新我們的分布了，讓這個曲線做一些移動去適應我們的新信息。beta分布在數學上就給我們提供了這一性質，他與二項分布是共軛先驗的（Conjugate_prior）。所謂共軛先驗就是先驗分布是beta分布，而后驗分布同樣是beta分布。結果很簡單：


\mbox{Beta}(\alpha_0+\mbox{hits}, \beta_0+\mbox{misses})

其中α0和β0是一開始的參數，在這里是81和219。所以在這一例子里，α增加了1(擊中了一次)。β沒有增加(沒有漏球)。這就是我們的新的beta分布Beta(81+1,219)，我們跟原來的比較一下：


可以看到這個分布其實沒多大變化，這是因為只打了1次球並不能說明什么問題。但是如果我們得到了更多的數據，假設一共打了300次，其中擊中了100次，200次沒擊中，那么這一新分布就是：


\mbox{beta}(81+100, 219+200)

注意到這個曲線變得更加尖，並且平移到了一個右邊的位置，表示比平均水平要高。

一個有趣的事情是，根據這個新的beta分布，我們可以得出他的數學期望為：\frac{\alpha}{\alpha+\beta}=\frac{82+100}{82+100+219+200}=.303，這一結果要比直接的估計要小 \frac{100}{100+200}=.333 。你可能已經意識到，我們事實上就是在這個運動員在擊球之前可以理解為他已經成功了81次，失敗了219次這樣一個先驗信息。

因此，對於一個我們不知道概率是什么，而又有一些合理的猜測時，beta分布能很好的作為一個表示概率的概率分布。

beta分布與二項分布的共軛先驗性質二項分布

二項分布即重復n次獨立的伯努利試驗。在每次試驗中只有兩種可能的結果，而且兩種結果發生與否互相對立，並且相互獨立，與其它各次試驗結果無關，事件發生與否的概率在每一次獨立試驗中都保持不變，則這一系列試驗總稱為n重伯努利實驗，當試驗次數為1時，二項分布服從0-1分布

二項分布的似然函數：


P(data|\theta) \propto \theta^z(1-\theta)^{N-z} \\ z=\sum_{i=1}^NX_i
beta分布
Beta(a,b)=\frac{\theta^{a-1}(1-\theta)^{b-1}}{B(a,b)}\propto \theta^{a-1}(1-\theta)^{b-1}


在beta分布中，B函數是一個標准化函數，它只是為了使得這個分布的概率密度積分等於1才加上的。

貝葉斯估計

我們做貝葉斯估計的目的就是要在給定數據的情況下求出θ的值，所以我們的目的是求解如下后驗概率：


P(\theta |data)=\frac{P(data|\theta)P(\theta)}{P(data)}\propto P(data|\theta)P(\theta)


注意到因為P(data)與我們所需要估計的θ是獨立的，因此我們可以不考慮它。

我們稱P(data|θ)為似然函數，P(θ)為先驗分布

共軛先驗

現在我們有了二項分布的似然函數和beta分布，現在我們將beta分布代進貝葉斯估計中的P(θ)中，將二項分布的似然函數代入P(data|θ)中，可以得到：


P(\theta |data) \propto \theta^z(1-\theta)^{N-z}*\theta^{a-1}(1-\theta)^{b-1} \\ \propto \theta^{a+z-1}(1-\theta)^{b+N-z-1}


我們設a′=a+z,b′=b+N−z
最后我們發現這個貝葉斯估計服從Beta(a’,b’)分布的，我們只要用B函數將它標准化就得到我們的后驗概率：


P(\theta |data)=\frac{\theta^{a'-1}(1-\theta)^{b'-1}}{B(a',b')}
參考資料：

1.Understanding the beta distribution (using baseball statistics)
2.20 - Beta conjugate prior to Binomial and Bernoulli likelihoods


作為分享主義者(sharism)，本人所有互聯網發布的圖文均遵從CC版權，轉載請保留作者信息並注明作者a358463121專欄: a358463121的專欄，如果涉及源代碼請注明GitHub地址： 358463121 (QJ) · GitHub。商業使用請聯系作者。
參考原文：

Beta Distribution

Beta Distribution Definition:

 

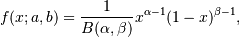
f(x; a,b) = \frac{1}{B(\alpha, \beta)} x^{\alpha - 1}(1 - x)^{\beta - 1},

這里，因為Beta分數是二項分布的參數p的概率分布, 所以x（即p）的取值范圍為0 <= x <= 1

where the normalisation, B, is thebeta function, Beta function could also be expressed by Gamma function:

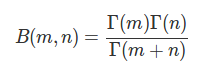
Gamma函數 在實數域可以表示為：

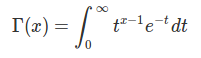
Gamma函數 在整數域可以表示為：

Γ(n)=(n−1)!

Gamma函數有以下性質：

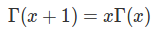
因為Beta函數可以表示為Gamma函數，所以Beta分布還可以表示為：

0 <= x <= 1

Beta分布可以理解為二項分布的參數p的分布，所以，這里重新定義Beta分布：

Beta分布的期望：

 

Beta分布的方差：

 

Beta分布的 眾數 mode:


 

Beta分布的偏度 Skewness：


 

Beta分布的 峰度 Kurtosis:


 

Beta Distribution Examples

Beta分布可以說是一個百變星君，根據參數a,b的不同，可以呈現出多種完全不同的概率分布圖.

生成Beta分布的代碼：

 

[python]  view plain  copy
 
 在CODE上查看代碼片派生到我的代碼片
  1. from scipy.stats import beta  
  2. import matplotlib.pyplot as plt  
  3. import numpy as np  
  4.   
  5. a, b = 2, 1  
  6.   
  7. mean, var, skew, kurt = beta.stats(a, b, moments='mvsk')  
  8.   
  9. x = np.linspace(0, 1, 100)  
  10. plt.plot(x, beta.pdf(x, a, b), 'r-', lw=5, alpha=0.6, label='beta pdf')  
  11. plt.show()  

 

然后，根據調整代碼中的a,b的取值，可以得到不同的Beta分布：

a, b = 2, 1:

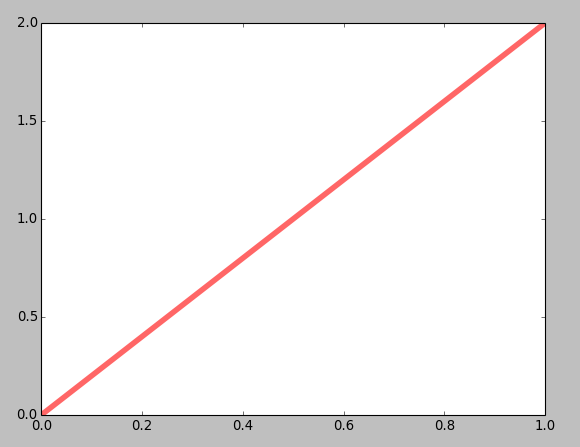
a, b = 2, 2

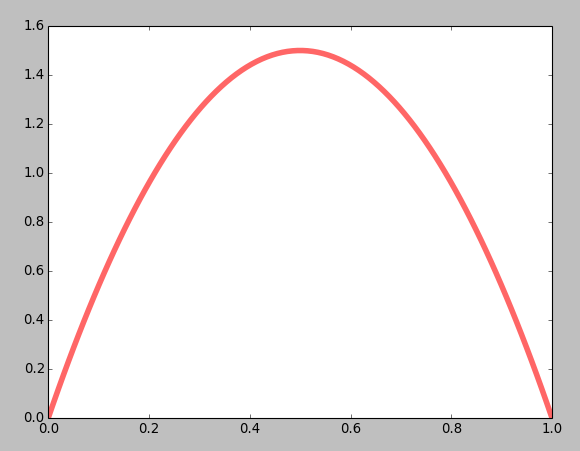
a, b = 8, 2

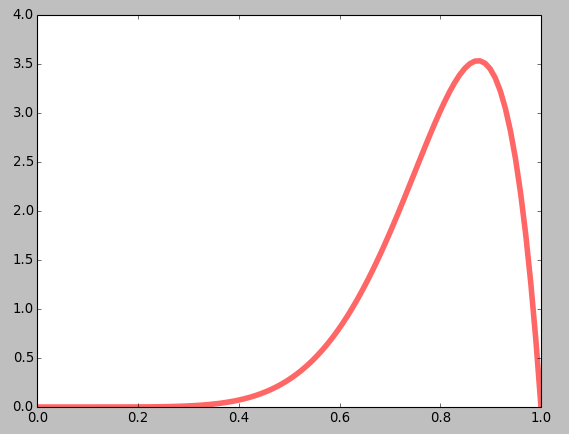
a, b = 0.01, 20

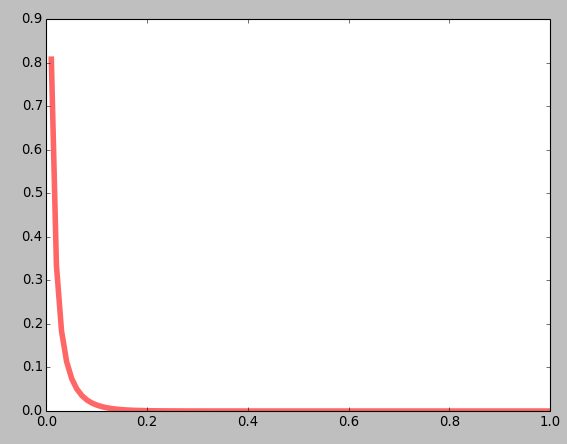
a, b = 1, 1

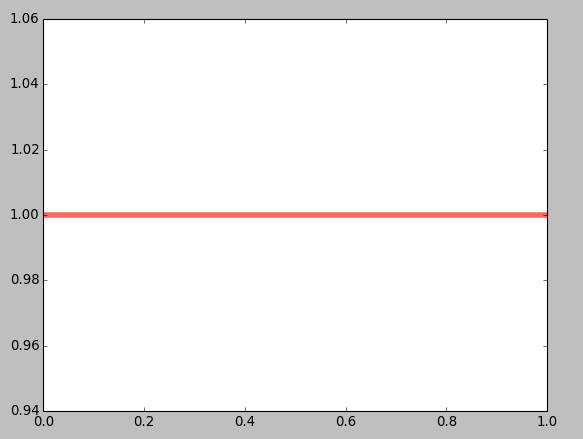
這樣一個一個的繪制，是不是太遜了， 畫在一起：

代碼：

 

[python]  view plain  copy
 
 在CODE上查看代碼片派生到我的代碼片
  1. from scipy.stats import beta  
  2. import matplotlib.pyplot as plt  
  3. import numpy as np  
  4.   
  5. x = np.linspace(0, 1, 100)  
  6.   
  7. a_array = [1, 2, 4, 8]  
  8. b_array = [1, 2, 4, 8]  
  9.   
  10. fig, axarr = plt.subplots(len(a_array), len(b_array))  
  11.   
  12. for i, a in enumerate(a_array):  
  13.   for j, b in enumerate(b_array):  
  14.     axarr[i, j].plot(x, beta.pdf(x, a, b), 'r', lw=1, alpha=0.6, label='a='+str(a)+',b='+str(b))  
  15.     axarr[i, j].legend(frameon=False)  
  16.   
  17. plt.show()  

 

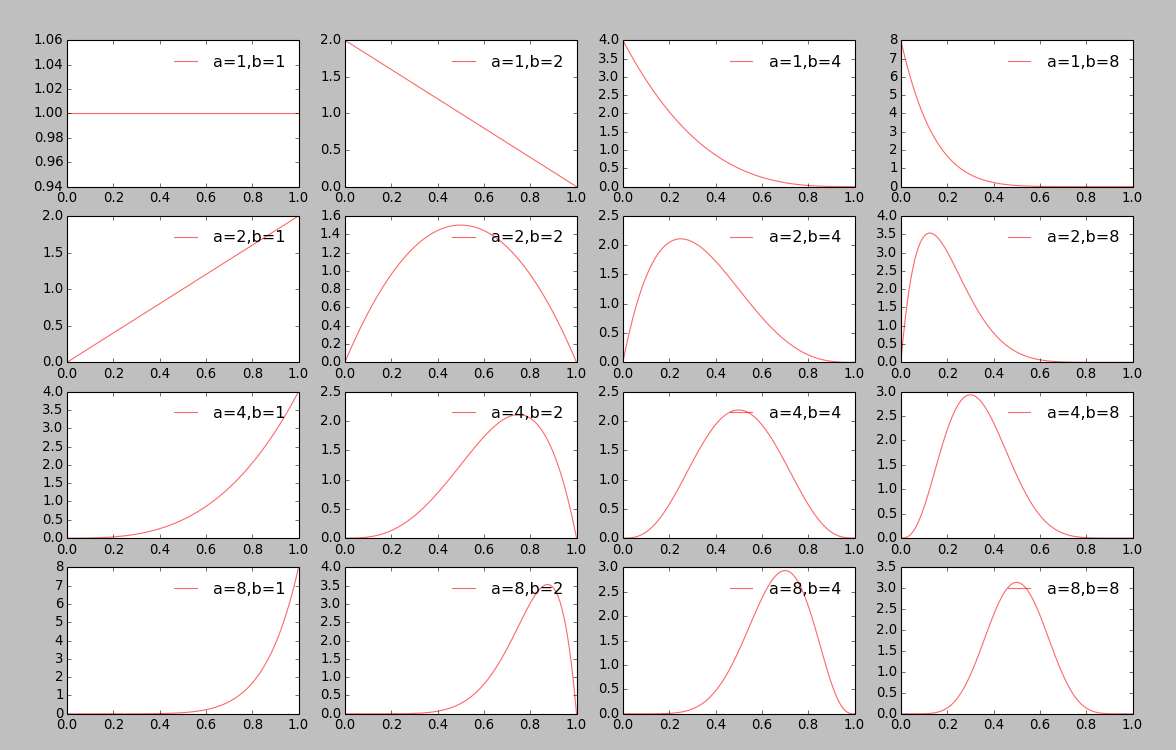
將所有的Beta分布繪制在一個圖上：

代碼：

 

[python]  view plain  copy
 
 在CODE上查看代碼片派生到我的代碼片
  1. from scipy.stats import beta  
  2. import matplotlib.pyplot as plt  
  3. import numpy as np  
  4.   
  5. x = np.linspace(0, 1, 100)  
  6.   
  7. a_array = [1, 2, 4, 8]  
  8. b_array = [1, 2, 4, 8]  
  9.   
  10. for i, a in enumerate(a_array):  
  11.   for j, b in enumerate(b_array):  
  12.     plt.plot(x, beta.pdf(x, a, b), lw=1, alpha=0.6, label='a='+str(a)+',b='+str(b))  
  13.   
  14. plt.legend(frameon=False)  
  15. plt.show()  

 

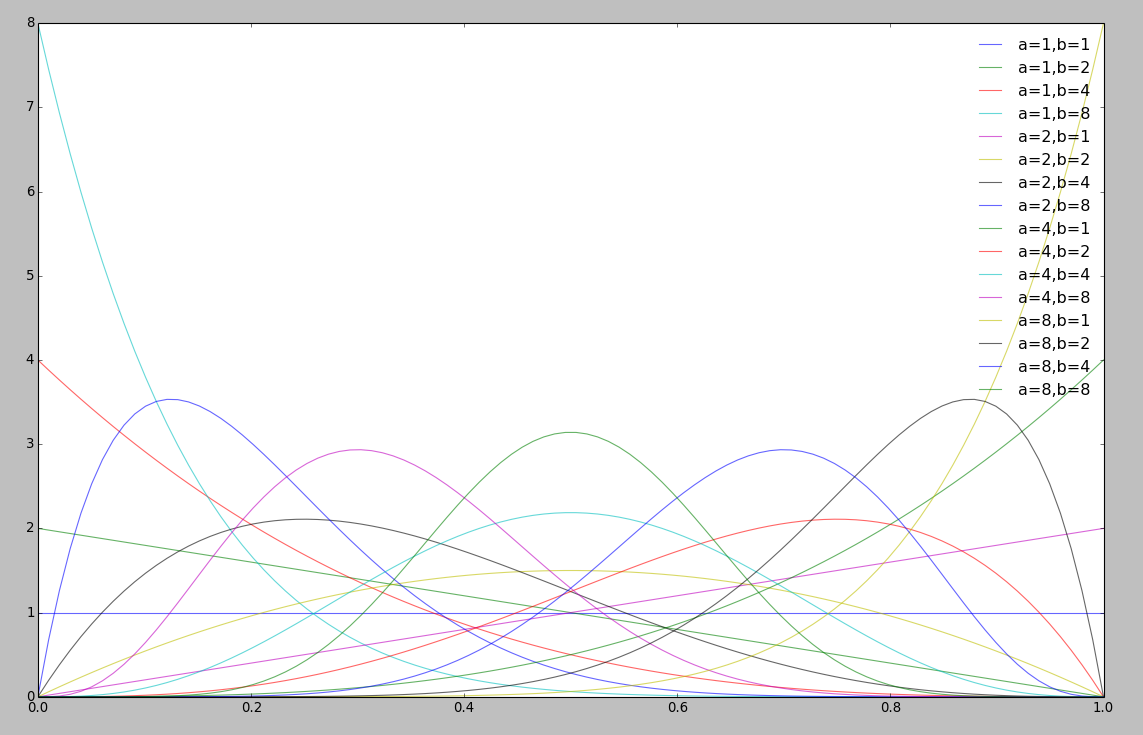
Beta Mean

由公式可以得到，Beta分布的均值，也可以通過采樣的方法，在一個Beta分布中，采樣，計算均值。

代碼：

 

[python]  view plain  copy
 
 在CODE上查看代碼片派生到我的代碼片
  1. import numpy as np  
  2. import numpy.random as nprnd  
  3. import scipy.stats as spstat  
  4. import scipy.special as ssp  
  5. import itertools as itt  
  6.   
  7. import matplotlib.pyplot as plt  
  8. import pylab as pl  
  9.   
  10. N = (np.arange(200) + 3) ** 2 * 20  
  11.   
  12. betamean = np.zeros_like(N, dtype=np.float64)  
  13.   
  14. for idx, i in enumerate(N):  
  15.     betamean[idx] = np.mean(nprnd.beta(2, 1, i))  
  16.   
  17. plt.plot(N, betamean, color='steelblue', lw=2)  
  18. plt.xscale('log')  
  19. plt.show()  
  20.   
  21. print spstat.beta(2, 1).mean()  
  22.   
  23. print spstat.beta(2, 1).mean(), 2.0 / (2 + 1)  
  24. print spstat.beta(2, 1).var(), 2 * 1.0 / (2 + 1 + 1) / (2 + 1) ** 2  

 

運行結果：

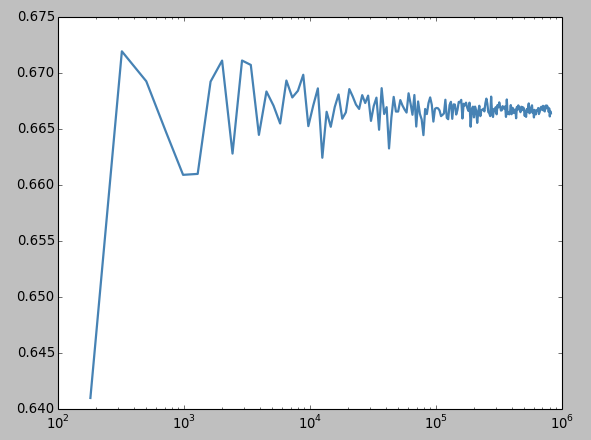
這里可以看到，隨着采樣點的增加，樣本點的均值也就更加的收斂，更加的接近⅔,  ⅔ 是一個通過公式計算得到的。 這樣，這個圖片的結果也符合大數定理，隨着采樣點的增加，只要樣本點無限大，那么最終的均值就會無限的接近⅔.

Conjugate Prior

A conjugate prior,p(p), of a likelihood, p(x|p), is a distribution that results in a posterior distribution, p(p|x)with the same functional form as the prior and a parameterisation that incorporates the observationx.

這句話，猛的一讀，暈頭轉向，但是，仔細讀上三五遍，基本上就理解了什么叫“共軛先驗”。

基本上說，一個參數的共軛先驗p(p)是這樣的一個分布：在這個分布的基礎上加上觀測樣本能夠得到一個與先驗分布具有相同的函數形式的后驗概率分布p(p|x)，並且這個后驗概率分布p(p|x)融合了觀測樣本x。也就是說共軛先驗p(p)和后驗概率分布p(p|x)具有相當的函數形式。

說點人話吧。。。

Beta分布是二項分布的參數p的共軛先驗，也就是說，二項分布的參數p的共軛先驗是一個Beta分布，其中，Beta分布中的兩個參數a,b可以看作兩個二項分布的參數p的先驗知識，可以稱為偽計數，例如 a, b = 2, 1, 這就意味着，二項分布的參數p的先驗知識為：在三次實驗中，a出現兩次，b出現1次，也可以理解為發生了2次，沒有發生的有1次。

后驗概率也符合Beta分布：

Beta(p|a, b) + count(m1, m2) = Beta(p| a+m1, b+m2)

在二項分布的參數的先驗分布的基礎上，加上觀測數據，就可以得到二項分布的參數p的后驗概率分布也符合Beta分布。這里， m1, m2 分別表示對應於 x=1 和 x=0在觀測數據中出現的次數。

話說，共軛先驗中的參數即Beta分布中的兩個參數a,b 是非常有意義的hyperparameter的解釋，前面已經提到了，a,b 可以理解為在觀測樣本 (m1, m2)的基礎上的先驗知識，或者可以理解為偽計數，即在我們的先驗知識中， x=1和x=0分別應該出現多少次，並且，這個先驗知識的取值，對於后驗概率的計算有比較大的影響。

二項分布的參數p的后驗概率分布仍然符合Beta分布可以通過下面的公式推到進行證明：

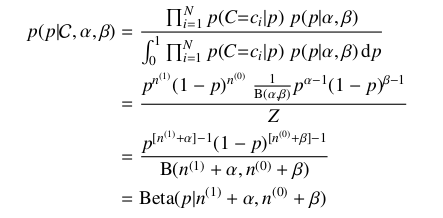
下面給出上面公式的推導過程：

假定集合C是服從N Bernoulli分布的一個集合，其中c=1或者c=0，那么可以根據貝葉斯參數估計計算集合C 的后驗參數估計：

 

所以，由上面的推導可以證明二項分布的參數p的后驗概率分布也服從Beta分布。

其中，上面公式中的Z可以進行如下推導：


 

 

公式2中用到了一個Beta分布的公式Beta函數：


 

所以，公式2中

 


免責聲明！

本站轉載的文章為個人學習借鑒使用，本站對版權不負任何法律責任。如果侵犯了您的隱私權益，請聯系本站郵箱yoyou2525@163.com刪除。



猜您在找 Beta分布 如何通俗理解 beta 分布？ beta 分布的簡單理解 二項分布和Beta分布 C++生成隨機數：Beta分布（beta distribution） 伯努利分布、二項分布、多項分布、Beta分布、Dirichlet分布 伯努利分布、二項分布、Beta分布、多項分布和Dirichlet分布與他們之間的關系，以及在LDA中的應用 （轉）Gamma分布，Beta分布，Multinomial多項式分布，Dirichlet狄利克雷分布 數理統計4：均勻分布的參數估計，次序統計量的分布，Beta分布 F-Beta-Score
 
粵ICP備18138465號   © 2018-2025 CODEPRJ.COM