感謝WHD的大力支持
最早知道網絡流的內容便是最大流問題,最大流問題很好理解:
解釋一定要通俗!
如右圖所示,有一個管道系統,節點{1,2,3,4},有向管道{A,B,C,D,E},即有向圖一張. [1]是源點,有無限的水量,[4]是匯點,管道容量如圖所示.試問[4]點最大可接收的水的流量?
這便是簡單的最大流問題,顯然[4]點的最大流量為50
死理性派請注意:流量是單位時間內的,總可以了吧!
然而對於復雜圖的最大流方法是什么呢,有EK,Dinic,SAP,etc.下面介紹Dinic算法(看代碼的直接點這)
Dinic 算法
Dinic算法的基本思路:
- 根據殘量網絡計算層次圖。
- 在層次圖中使用DFS進行增廣直到不存在增廣路
- 重復以上步驟直到無法增廣
引自NOCOW,相當簡單是吧…
小貼士:
一般情況下在Dinic算法中,我們只記錄某一邊的剩余流量.
- 殘量網絡:包含反向弧的有向圖,Dinic要循環的,每次修改過的圖都是殘量網絡,
- 層次圖:分層圖,以[從原點到某點的最短距離]分層的圖,距離相等的為一層,(比如上圖的分層為{1},{2,4},{3})
- DFS:這個就不用說了吧…
- 增廣 :在現有流量基礎上發現新的路徑,擴大發現的最大流量(注意:增加量不一定是這條路徑的流量,而是新的流量與上次流量之差)
- 增廣路:在現有流量基礎上發現的新路徑.(快來找茬,和上一條有何不同?)
- 剩余流量:當一條邊被增廣之后(即它是增廣路的一部分,或者說增廣路通過這條邊),這條邊還能通過的流量.
- 反向弧:我們在Dinic算法中,對於一條有向邊,我們需要建立另一條反向邊(弧),當正向(輸入數據)邊剩余流量減少I時,反向弧剩余流量增加I
Comzyh的較詳細解釋(流程) :
- 用BFS建立分層圖 注意:分層圖是以當前圖為基礎建立的,所以要重復建立分層圖
- 用DFS的方法尋找一條由源點到匯點的路徑,獲得這條路徑的流量I 根據這條路徑修改整個圖,將所經之處正向邊流量減少I,反向邊流量增加I,注意I是非負數
- 重復步驟2,直到DFS找不到新的路徑時,重復步驟1
注意(可以無視):
- Dinic(其實其他的好多)算法中尋找到增廣路后要將反向邊增加I
- Dinic中DFS時只在分層圖中DFS,意思是說DFS的下一個節點的Dis(距源點的距離)要比自己的Dis大1,例如在圖1中第一個次DFS中,1->2->4 這條路徑是不合法的,因為Dis[2]=1;Dis[4]=1;
- 步驟2中“獲得這條路徑的流量I “實現:DFS函數有參量low,代表從源點到現在最窄的(剩余流量最小)的邊的剩余流量,當DFS到匯點是,Low便是我們要的流量I
對於反向弧(反向邊)的理解:
這一段不理解也不是不可以,對於會寫算法沒什么幫助,如果你着急,直接無視即可.
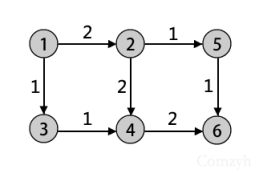
先舉一個例子(如右圖):
在這幅圖中我們首先要增廣1->2->4->6,這時可以獲得一個容量為2的流,但是如果不建立4->2反向弧的話,則無法進一步增廣,最終答案為2,顯然是不對的,然而如果建立了反向弧4->2,則第二次能進行1->3->4->2->5->6的增廣,最大流為3.
Comzyh對反向弧的理解可以說是”偷梁換柱“,請仔細閱讀:在上面的例子中,我們可以看出,最終結果是1->2->5->6和1->2->4->6和1->3->4->6.當增廣完1->2->4->5(代號A)后,在增廣1->3->4->2->5->6(代號B),相當於將經過節點2的A流從中截流1(總共是2)走2->5>6,而不走2->4>6了,同時B流也從節點4截流出1(總共是1)走4->6而不是4->2->5->6,相當於AB流做加法.
簡單的說反向弧為今后提供反悔的機會,讓前面不走這條路而走別的路.
Alwa同學非要我給他的文章加一個鏈接,大家可以看看他的文章: 有關網絡流中的反向弧和增廣路