一、准经典模型
1. 经典处理
- 经典处理:电子的行为能用牛顿定律处理。
- Drude模型用了经典处理。(sommerfeld模型不是,sommerfeld模型是用薛定谔方程处理电子)
- 在很多问题中经典处理是很好的近似的原因:北大书第15页(+注1)
2. 准经典模型
- 在Drude模型(完全的经典模型)中,电子的速度取平均热运动速度\(v _ { th }\),由能量均分定理\(\frac{1}{2}mv _ { th } ^ { 2 }=\frac{3}{2}k _ { B } T\)得:\(v _ { th } ^ { 2 } \approx k _ { B } T / m\)
- 在sommerfeld模型中,几乎完全保留了Drude模型中的所有假设,只作了两点修正,一是电子在每个量子态上的分布由费米-狄拉克统计(全同粒子,泡利不相容原理,费米分布函数)决定,二是金属中传导电子的量子态由薛定谔方程决定。
- 准经典模型:
用经典处理,采取牛顿定律,但是也使用费米狄拉克统计得到的费米面,费米速度等这些概念,只有费米面附近的电子对电流有贡献,故这些对电流有贡献的电子的速度的大小近似为费米速度(速度方向不同)。
二、Drude模型(完全的经典模型)求电导率
- 复习:河北师大书18至20页
电子的漂移速度:t时刻电子的恒定的平均的速度v(t)
平均的含义:碰撞和未碰撞的电子都考虑了
三、准经典模型求电导率
-
复习:河北师大书 20至22页
-
补充1:

-
补充2:(下面的一段话“近似估计认为......"非常重要,必须复习!)

-
补充3:费米面的漂移一般很小:课件
-
没时间就不复习:《solid state》第二章 sommerfeld模型 第52、53页



在第13章当修正的费米分布被使用,加上能量依赖的弛豫时间,会使金属的很多性质产生量子力学的影响。
四、金属的交流电导率
未学
五、金属的热导率
- 河北师大书22页
- 补充1:划线

- 补充2:(1.4.35)式下面一段话“电子的速度应取为费米速度”的补充:
在准经典模型中,由热学中气体分子动理论,也可得到和Drude模型中相同的热导率表达式:
\[\kappa = \frac { 1 } { 3 } c _{v} v l = \frac { 1 } { 3 } c_{v} v ^ { 2 } \tau\tag{1.4.35} \]
虽然准经典模型和Drude模型有差别【差别在于电子浓度(只有费米面附近的电子被热激发)和电子的平均速度(这些电子的速度近似都取为沿热流方向(不知道是否正确,应该查《solid state》或热学书中气体分子动理论推导热导率的过程)的大小为\(v_{F}\)的一个速度】,但此式和Drude模型中的热导率表达式相同,这是因为电子浓度的差别体现在热容中,由于热容和电子速度的差别,所以将热容改为量子理论的表达式,v改为,\(\tau\)改为\(\tau_{F}\),计算得热导率表达式:$$
\kappa = \frac { \pi ^ { 2 } k _{B}^ { 2 } n \tau _ { F } } { 3 m _ { e } } T\tag{1.4.36}
\[ ###六、热电子发射和接触电势 - 复习:课件 ###七、金属的霍尔效应和磁致电阻 - 河北师范书24页 - 补充1:  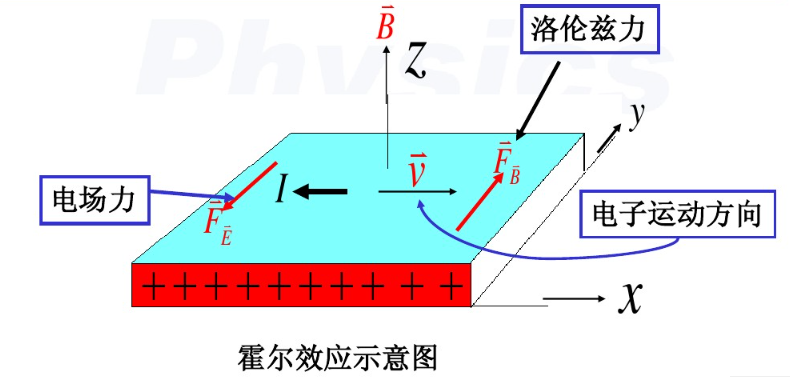 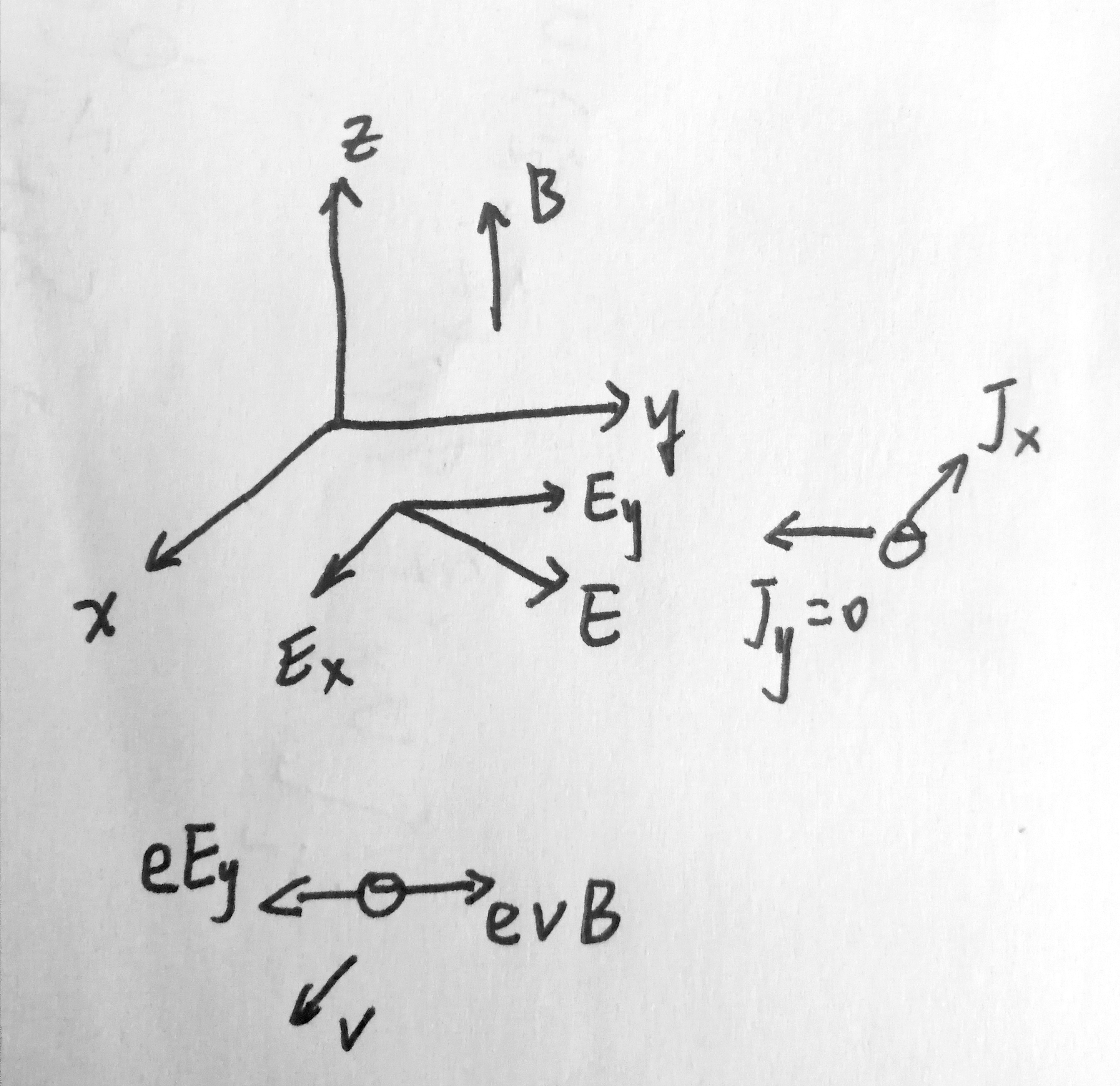 - 补充2:  - 磁致电阻未学,河北师大书 *** <span id = "jump">注1:还有原因见《solid state》:因此,经典力学可以很好地描述金属电子行为的现象范围很广。然而,这并不能立即证明N个这样的电子的行为可以用经典力学来描述。因为泡利不相容原理对N个电子,为什么它不应该对它们的动力学产生同样剧烈的影响呢?它并不遵循一个基本定理,我们不需要证明它,因为这个证明虽然简单,但在标记上却相当繁琐等。这些不重要,所以不复习</span> <br/><br/> --- <center>参考文献</center> 1.《固体物理基础》孙会元 2.河北师大孙会元老师的固体物理课件 3.《固体物理基础》阎守胜 4.《固体物理学》朱建国等 5.《solid state physics》Mermin 本文图片也来源于以上2、3、4、5这四种资料 6.中科大赵瑾老师的固体物理课件 7.慕课:北京交通大学 李丹 固体物理学 8.北京大学固体物理课件:http://www.doc88.com/p-1466697881134.html <br/><br/>                                                        ---本文由量子凝聚态编写                                                           (转载需注明来源)\]
