單、雙緩沖區學習筆記

緩沖區數據傳輸時間計算

單緩沖區

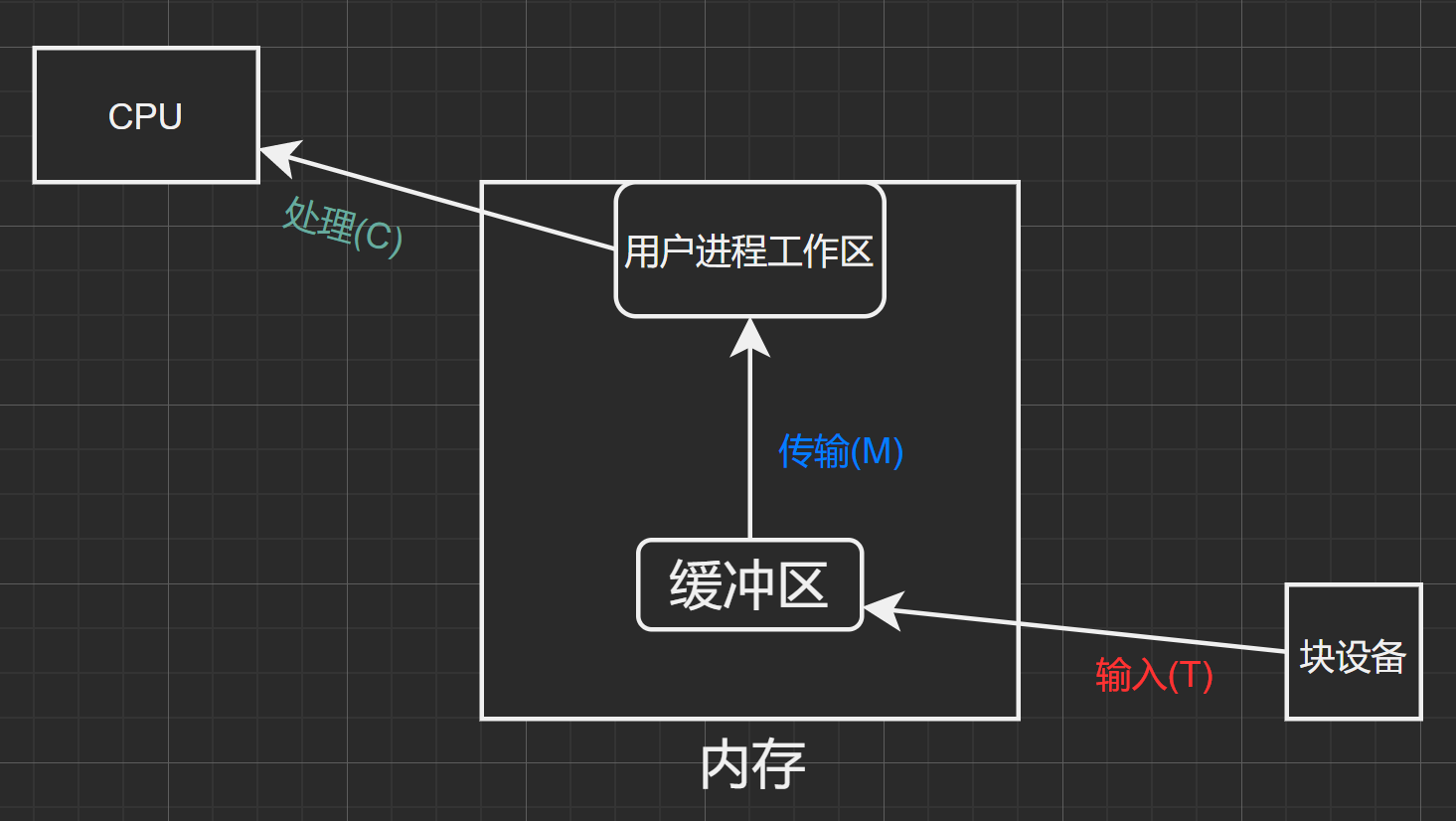圖1.1

其中數據流之間的關系為：圖1.2

• 這與緩沖區的特性有關，只有當緩沖區內為空時才能往里面傳入數據；只有緩沖區為滿時才能從中取出數據。

  也意味着，對於緩沖區來說，同一時刻只能存在輸入(T)與傳輸(M)中的一個操作。但是輸入(T)與處理(C)操作可以同時存在。

處理時間(C) > 輸入時間(T)的情況：

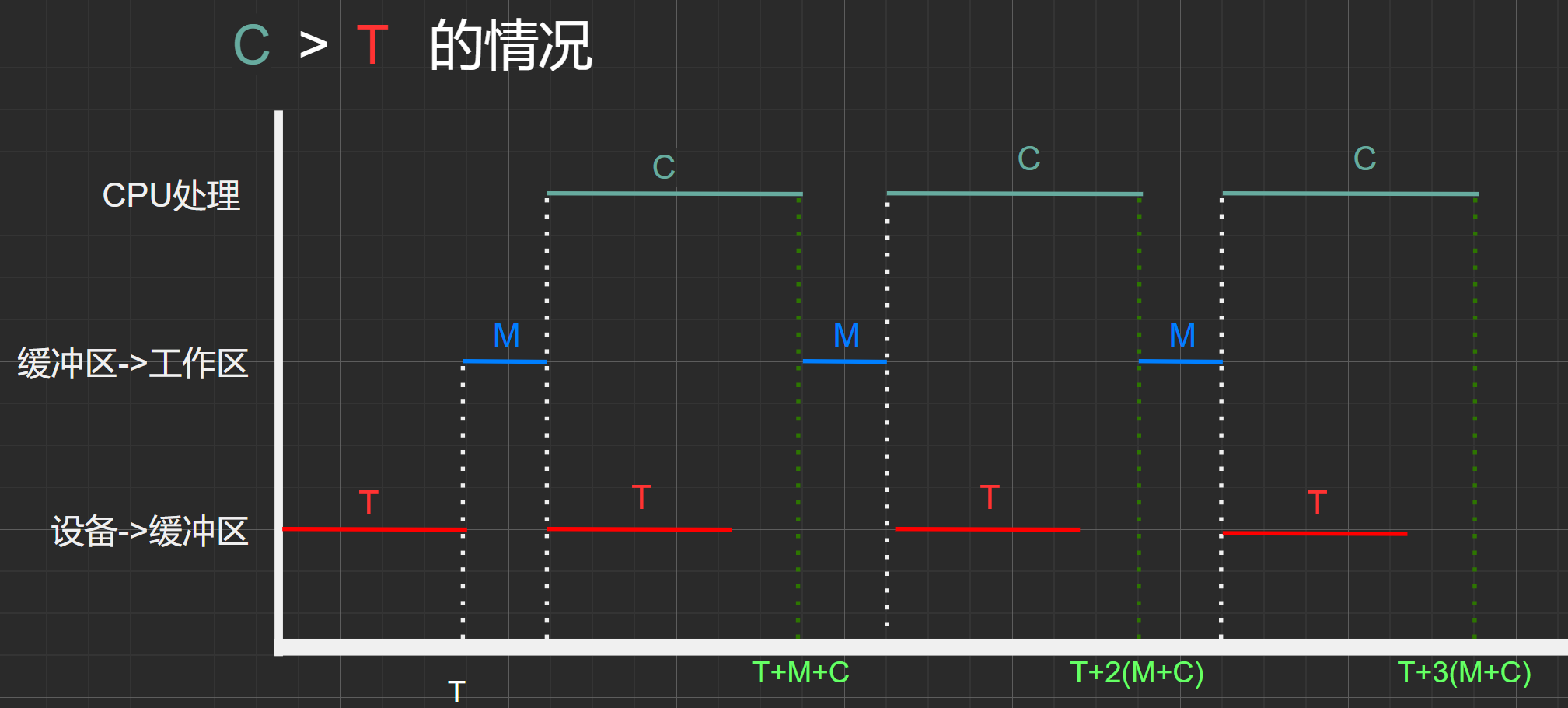圖1.3

假設初始0時刻狀態：緩沖區、工作區均為空。

這里稍微解釋一下這甘特圖的含義。從一開始經過T時間之后，緩沖區被充滿了第一塊數據。之后經過M時間后，該數據塊從緩沖區傳輸到工作區。再經過C時間，該數據塊在用戶空間內被CPU處理，而從上面的 [數據流之間的關系] 圖可以得知，在CPU處理該數據塊時，可以並行的從設備中接着輸入下一塊數據塊到緩沖區中(在CPU剛開始處理數據塊時緩沖區為空)，而由於C>T所以在CPU處理完上一塊數據時，緩沖區已經被充滿下一塊數據。從上面的 [數據流之間的關系] 圖可以得知C操作與M操作只能串行，即在工作區未完全為空時不能提前將緩沖區中的數據傳輸到工作區，所以下一個M需要等待C執行完畢之后才能進行。后面的過程與此類似。

這里可以一個周期為單位來分析數據塊的處理情況(一塊數據塊從設備->緩沖區->工作區->cup處理)，一個周期：下一次達到當前狀態時所需經過的最少時間。

如：

• \(T\)時間點：緩沖區為滿，工作區為空
• \(T+M+C\)時間點：緩沖區為滿，工作區為空，狀態與時刻\(T\)相同
• 可得，時間：\((T+M+C)-T=M+C\) 為一個周期，其中處理了一個數據塊（C）
• 因此，在處理時間(C) > 輸入時間(T)的情況下，平均處理一個數據塊所需時間為\(M+C\)

按照上面的推理，我們可知道，當時間點為：\(T+2(M+C)\)時，以及處理了兩個數據塊。

碎碎念：雖然僅僅從一塊數據塊的從設備->緩沖區->工作區->cup處理的時間為\(0\)~\((T+M+C)\) 很容易讓人以為兩塊數據塊的處理時間為\(2*(T+M+C)\)，我做題就這么算錯了 ，實際上為\(T+2(M+C)\) ，為什么不能這么算呢？因為對於連續處理數據快來說，相鄰的兩個周期內有一段時間是重合的。

處理時間(C) < 輸入時間(T)的情況：

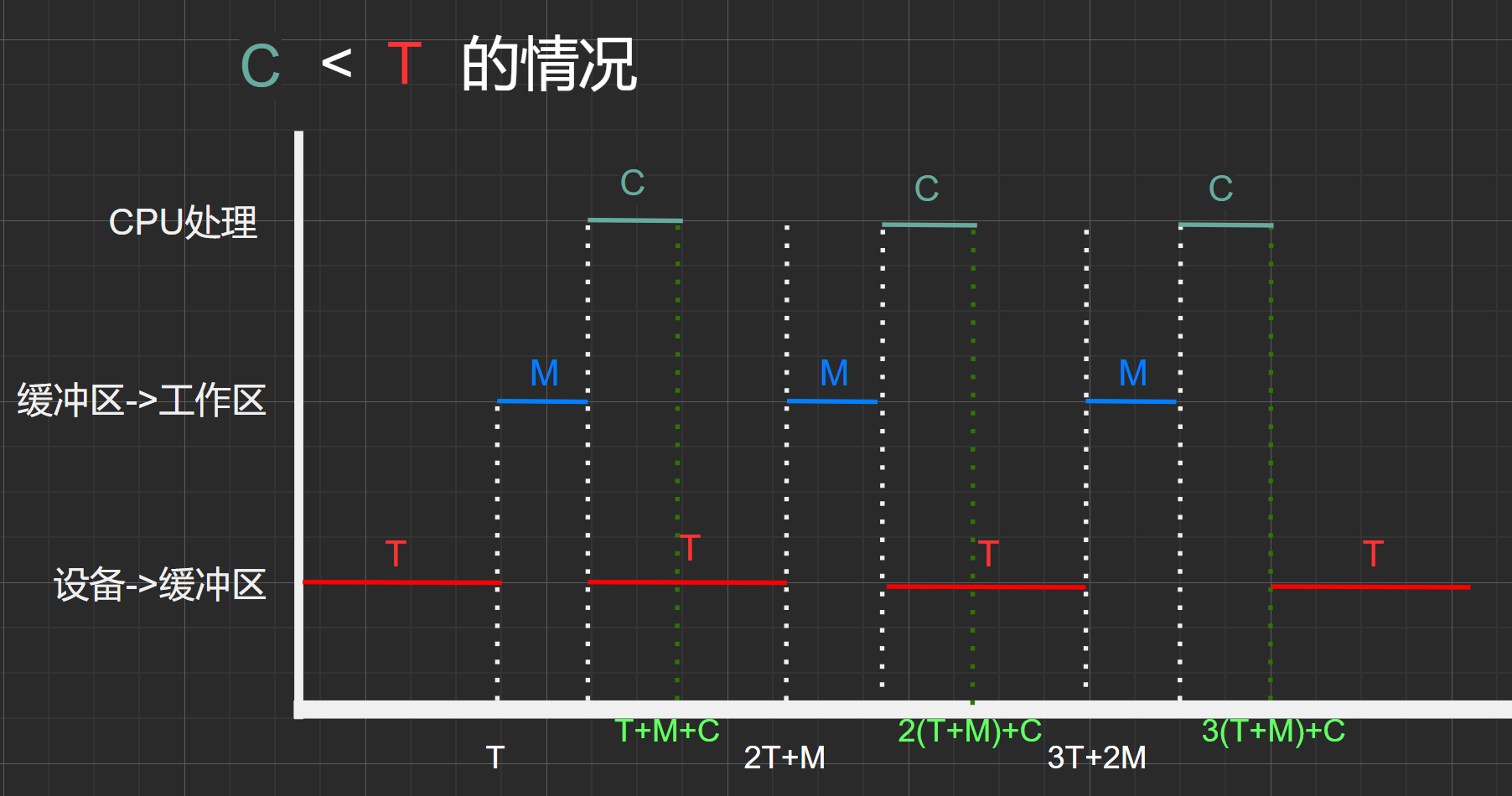圖1.4

同上面情況類型。

從一開始經過T時間之后，緩沖區被充滿了第一塊數據。之后經過M時間后，該數據塊從緩沖區傳輸到工作區。再經過C時間，該數據塊在用戶空間內被CPU處理，而從上面的 [數據流之間的關系] 圖可以得知，在CPU處理該數據塊時，可以並行的從設備中接着輸入下一塊數據塊到緩沖區中(在CPU剛開始處理數據塊時緩沖區為空)，而由於C<T所以在CPU處理完上一塊數據時，緩沖區還未傳輸完下一塊數據。

假設初始0時刻狀態：緩沖區、工作區均為空。

• \(T\)時間點：緩沖區為滿，工作區為空
• \(2T+M\)時間點：緩沖區為滿，工作區為空，狀態與時刻\(T\)相同
• 可得，時間：\((2T+M)-T=T+C\) 為一個周期，其中處理了一個數據塊（C）
• 因此，在處理時間(C) < 輸入時間(T)的情況下，平均處理一個數據塊所需時間為\(T+C\)

碎碎念：類似於上情況的碎碎念，不過需要注意的是，這里所要求處理第二個數據塊的時間所以不應該包括第三個\(T\)，因為那個\(T\)是屬於第三個數據塊周期的。所以該情況下處理兩個塊的耗時為：\(2*(T+M)+C\)

找關系，單緩沖區平均處理一個數據塊耗時

圖1.5

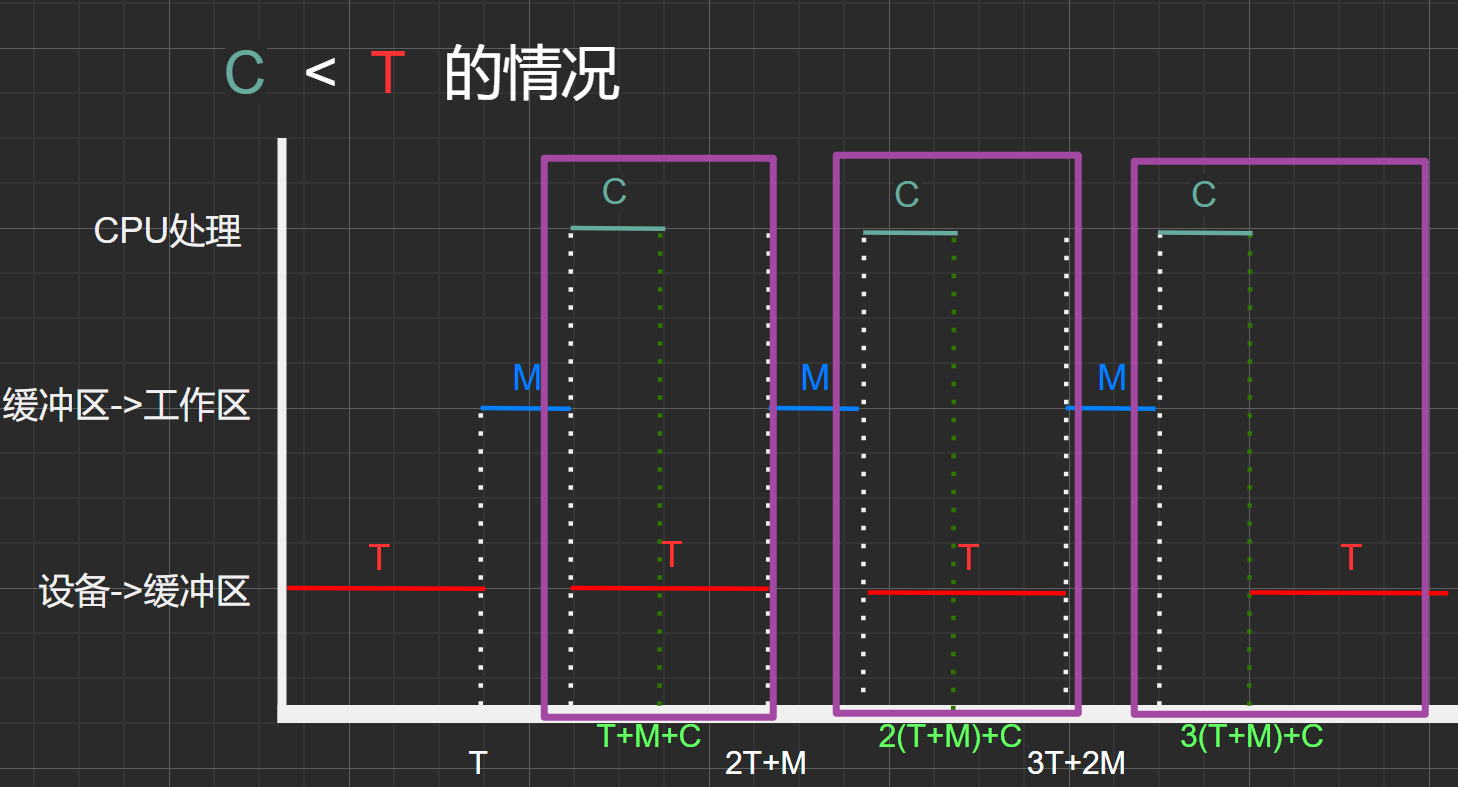圖1.6

仔細觀察上圖，不難發現這個現象：每個周期內，區間總時間內有一部分是重疊，且時間取最大值：\(MAX(C,T)\)

這里並不難理解，因為這兩個操作是並行的，也就是說可以同時進行。但是作為周期循環的中間媒介 緩沖區的相關操作M與這兩個操作又是串行的，因此需要單獨算上該時間。

**因此，不論是 C>T 還是 C<T ,緩沖區平均處理一個數據塊的時間為：\(MAX(C,T)+M\) **

看到這結論時，估計大家會想起我在上面碎碎念時談到關於處理兩個數據塊的耗時問題，會很自然的想處理兩個數據塊的耗時是不是可以直接\(2*[MAX(C,T)+M]\)呢？但是實際上兩種情況中處理兩個數據塊無論是哪一個情況都不符合這結果。

因為我們所求時間為：\(設備->緩沖區->工作區->CPU處理\)

與我們求公式時選定的周期時間：\(緩沖區->工作區->MAX(CPU處理,設備->緩沖區)\)

不一致。

接下來讓我們找一找內在聯系

圖1.7

可以看出，\([0,T+3(M+C)]\) 內處理了三個數據塊。

所需時間 =\(T+M+MAX(C,T)+M+MAX(C,T)+M+C\)

=\(T+M+C+2[M+MAX(C,T)]\)

=\(T+M+MAX(C,T)+2[M+MAX(C,T)]\)

=\(3[M+MAX(C,T)]+T\)

=>\(N*緩沖區平均處理一塊數據塊時間+T\)，其中N為處理的數據塊數

=\(3*(M+C)+T\)

用該公式求解碎碎念：

將公式中的3改成2即可得到答案。

圖1.8

可以看出，\([0,C+3(M+C)]\) 內處理了三個數據塊。

所需時間：\(T+M+MAX(C,T)+M+MAX(C,T)+M+C\)

=\(T+M+C+2[M+MAX(C,T)]\)

=\(MAX(C,T)+M+C+2[M+MAX(C,T)]\)

=\(3[M+MAX(C,T)]+C\)

=>\(N*緩沖區平均處理一塊數據塊時間+C\)，其中N為處理的數據塊數

=\(3*(M+T)+C\)

用該公式求解碎碎念：

將公式中的3改成2即可得到答案。

再總結：

求N塊數據塊從設備->緩沖區->工作區->cup處理所需的時間。

\(N*[M+MAX(C,T)]+min(C,T)\)

\(=處理數據塊的數量*[緩沖區->工作區+MAX(CPU處理,設備->緩沖區)]+min(CPU處理,設備->緩沖區)\)

例題：

設系統緩沖區和用戶工作區均采用單緩沖，從外設讀入一個數據塊到系統緩沖區的時間為\(100\)，從系統緩沖區讀入一個數據塊到用戶工作區的時間為\(5\)，對用戶工作區中的一個數據塊進行分析的時間為\(90\)（如下圖）。進程從外設讀入並分析\(2\)個數據塊的最短時間為多少？

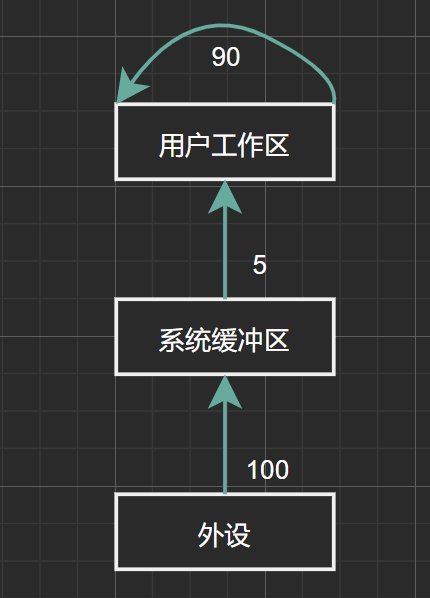圖1.11

時間甘特圖：

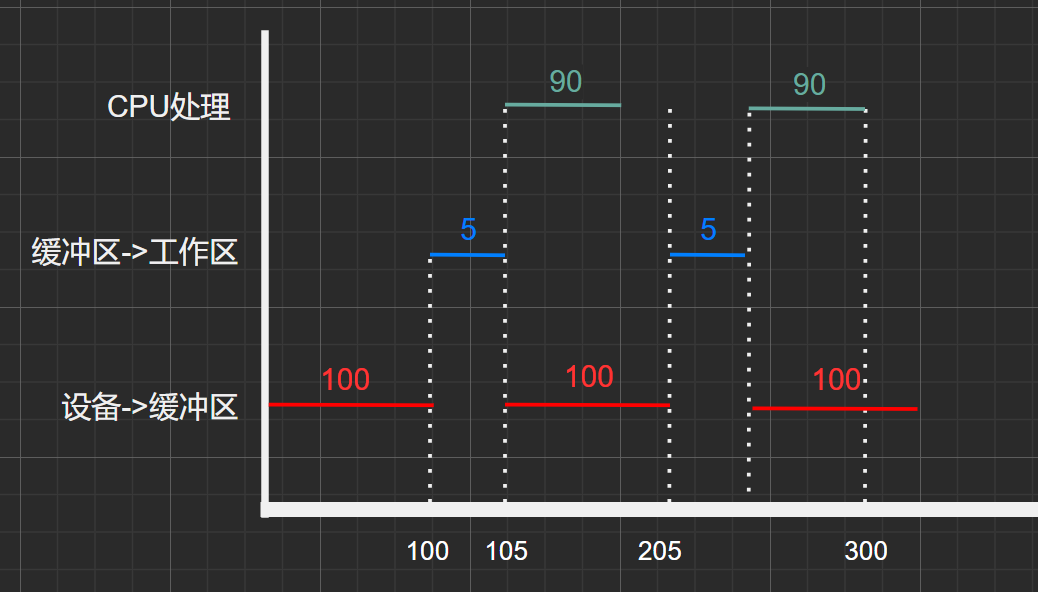圖1.12

單緩沖區，套用公式：\(N*[M+MAX(C,T)]+min(C,T)\)

得： \(2*(5+100)+90=300\)

雙緩沖區：

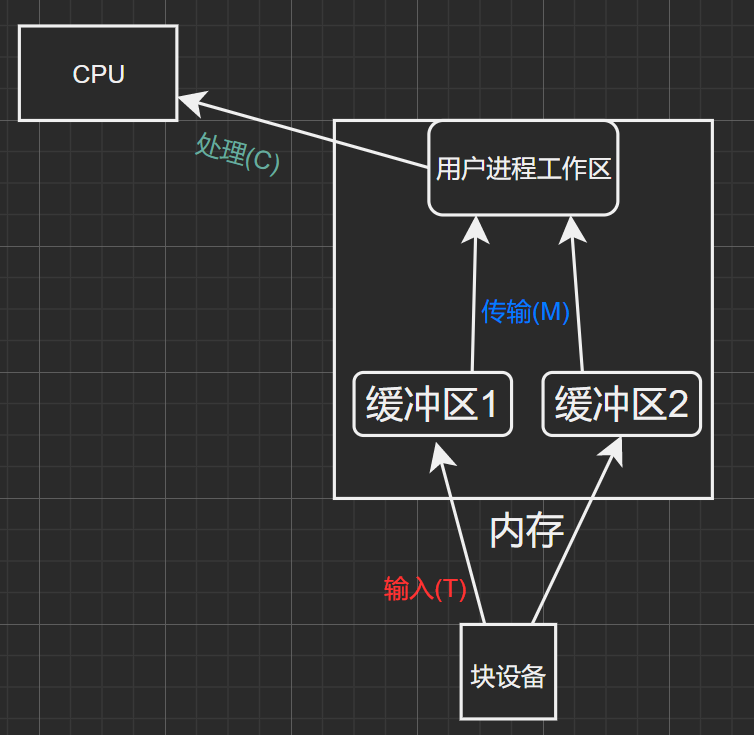圖2.1

其中數據流之間的關系為：圖2.2

注意這里的T2、T1的速度相同，M1、M2的速度相同

處理時間(C)+傳送時間(M) < 處理時間(C)的情況：

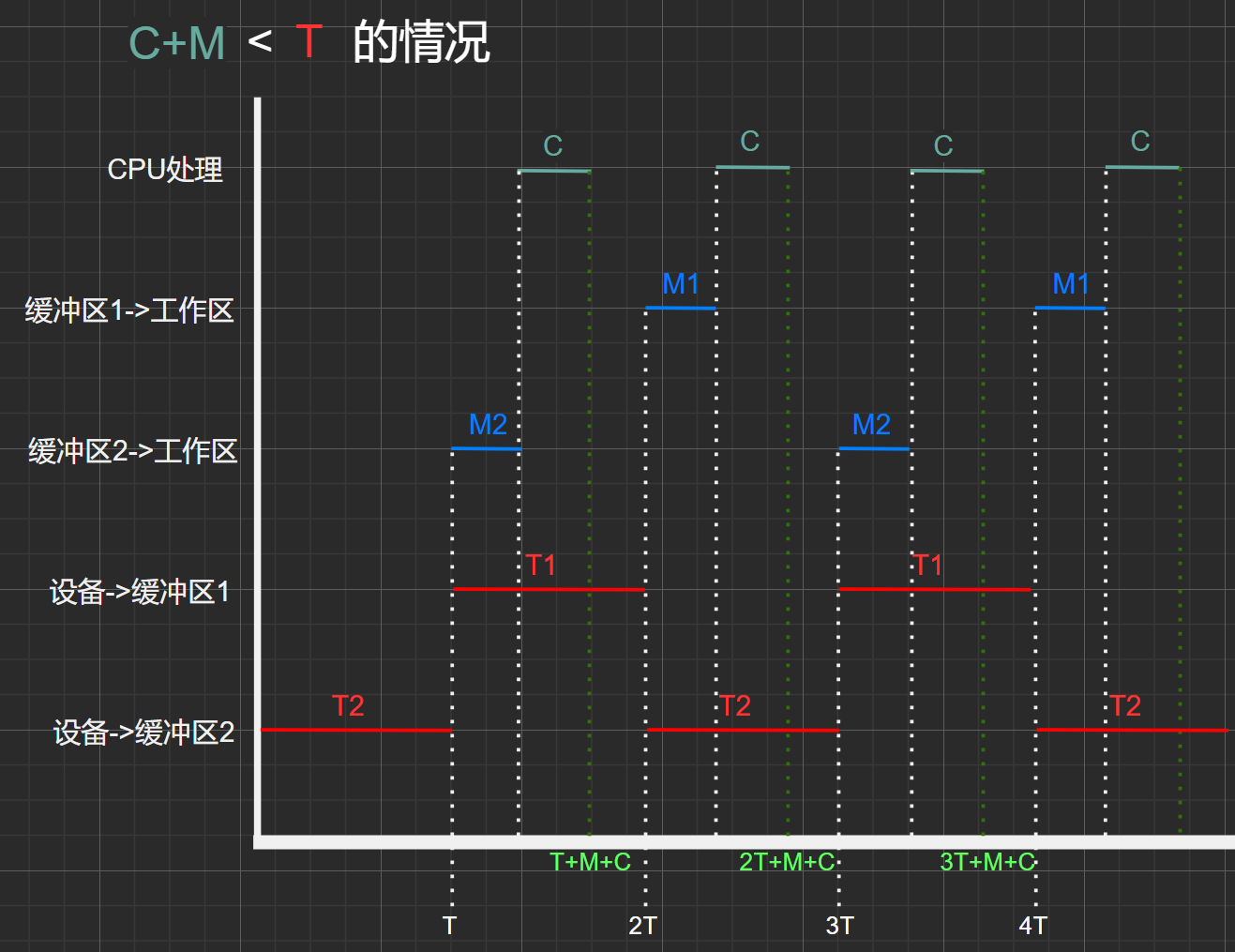圖2.3

初始狀態：0時刻中工作區，緩沖區1、緩沖區2均為空

這里的分析情況與單緩沖類似。

• \(T時間點：\) 工作區為空、緩沖區2為滿、緩沖區1為空
• \(2T時間點：\) 工作區為空、緩沖區2為空、緩沖區1為滿
• \(3T時間點：\)工作區為空、緩沖區2為滿、緩沖區1為空，達到了\(T時間點\)的相同狀態，因此
• 可得，時間\(3T-T=2T\)為一個周期，其中處理了兩個數據塊(C)
• 因此，在處理時間(C)+傳送時間(M) < 處理時間(C)的情況下，平均處理一個數據塊所需時間為：\(2T/2=T\)

其實，這兩個緩沖區的處理速度一樣，可以將其等效，即將\(T、2T、3T\)時間點看成相同的狀態：工作區為空，一個緩沖區為滿、一個緩沖區為空。

也就是說，\(2T\) ~ \(T\)可看作一個周期

處理時間(C)+傳送時間(M) > 處理時間(C)的情況：

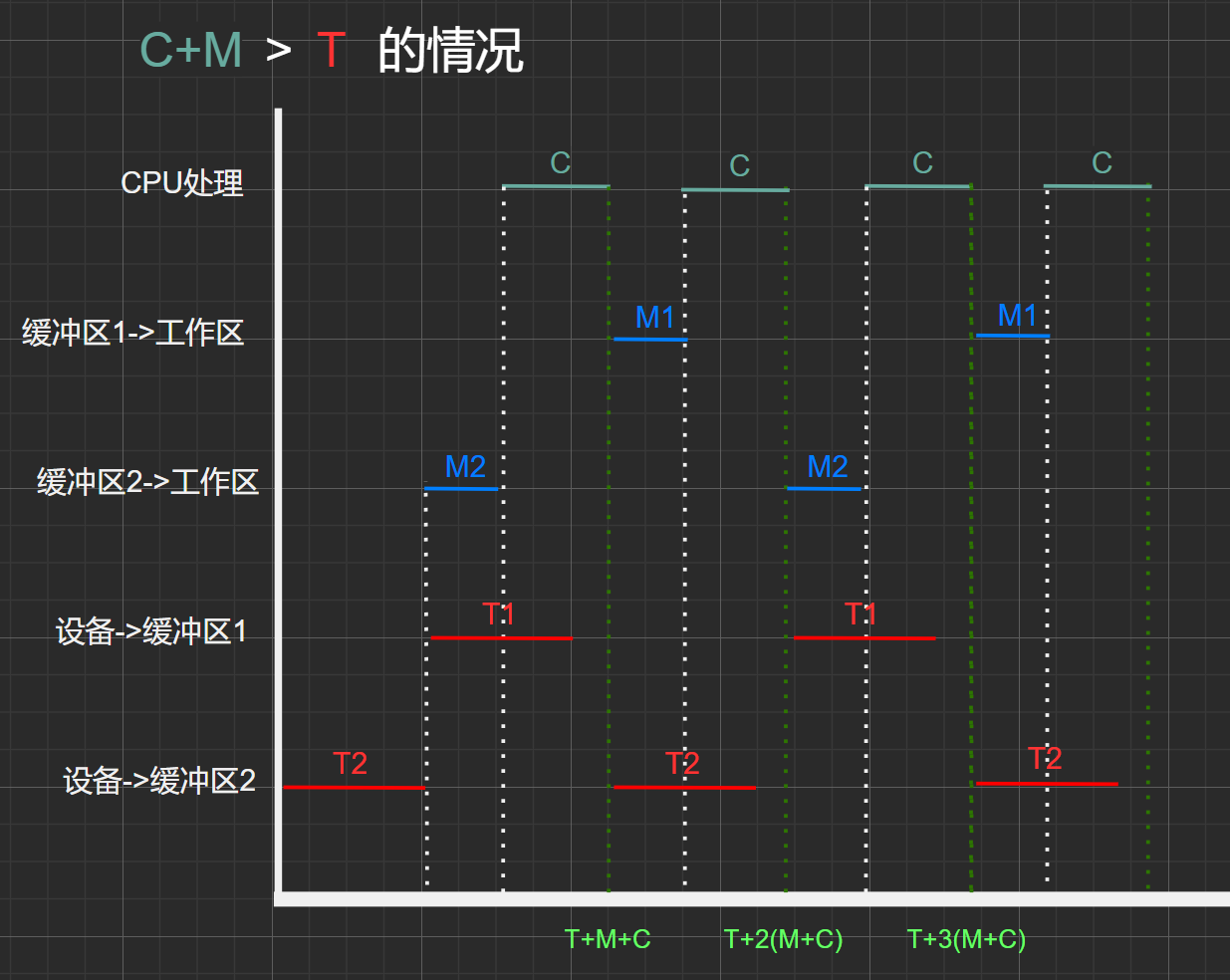圖2.4

初始狀態：0時刻中工作區，緩沖區1、緩沖區2均為空

• \(T時刻\)：工作區為空、緩沖區2為滿、緩沖區1為空
• \(T+M+C時刻：\) 工作區為空、緩沖區2為空、緩沖區1為滿
• \(T+2(M+C)時刻：\)工作區為空、緩沖區2為滿、緩沖區1為空，達到了\(T時刻\)相同的狀態，因此
• 可得，時間\([T+2(M+C)]-T = 2(M+C)\)為一周期，其中處理了兩個數據塊(C)
• 因此，在處理時間(C)+傳送時間(M) > 處理時間(C)的情況下，平均處理一個數據塊所需時間為：\(2(M+C)/2=M+C\)

同理，可將\(T、2T、3T\)時間點看成相同的狀態：工作區為空，一個緩沖區為滿、一個緩沖區為空。

也就是說，\(2T\) ~ \(T\)可看作一個周期

找規律：

仔細觀察，會發現，這雙緩沖區與單緩沖區類似，每個周期內，區間總時間內有一部分是重疊，且時間取最大值：\(MAX(C+M,T)\) ，而取這最大值的區域剛好為一個周期范圍，同時包括了三種操作。因此可得一個周期的時間為該最大值，且在這時間內剛好處理了一塊數據塊。

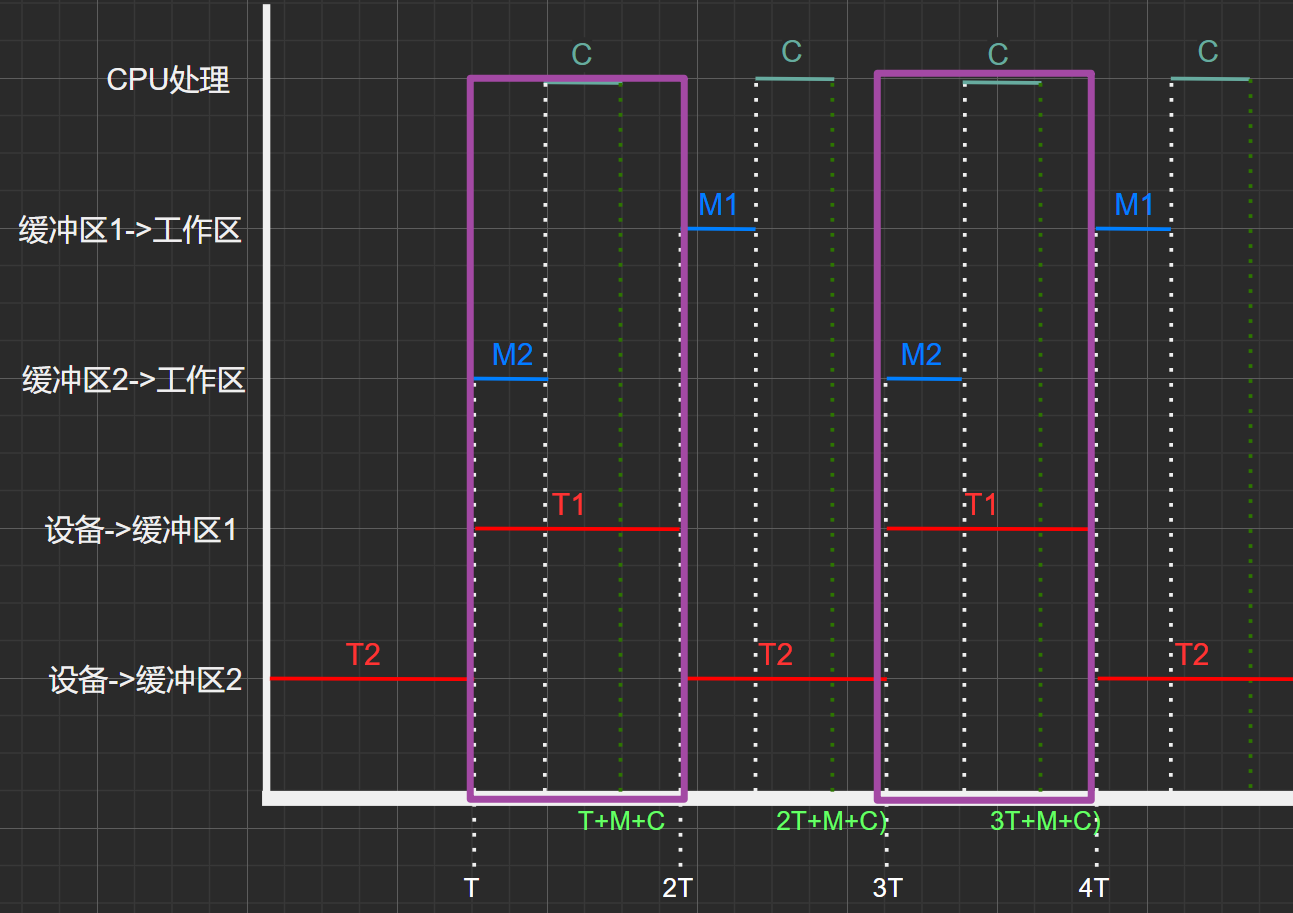圖2.5

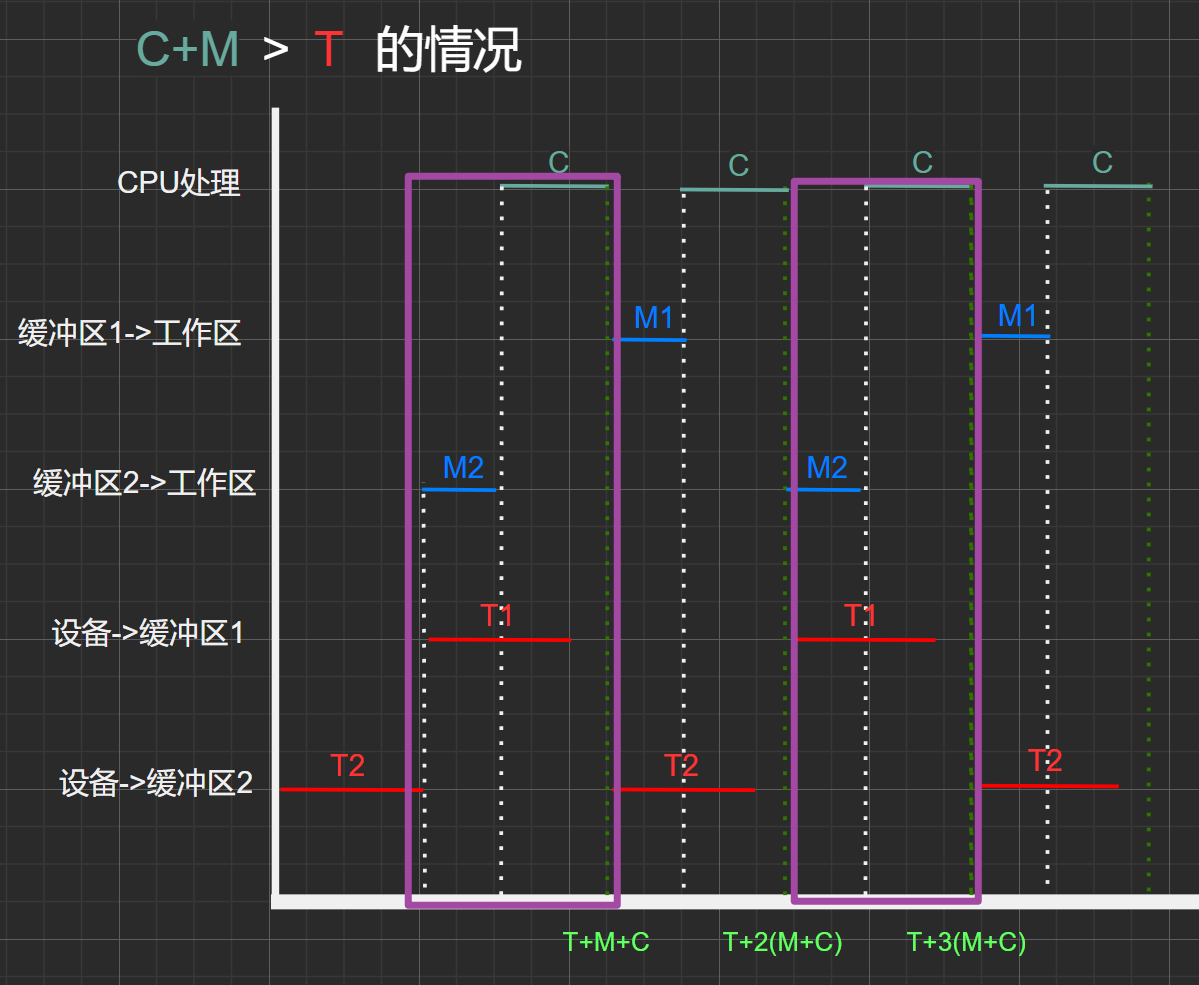圖2.6

**因此，不論是 (C+M)>T 還是 (C+M)<T ,緩沖區平均處理一個數據塊的時間為：\(MAX(C+M,T)\) **

類似於單緩沖區中的問題，讓我們來看一下\(N\)塊數據塊的從設備->緩沖區->工作區->cup處理的時間要多少。

從圖中可以很明顯的看出所需時間為：\(T+M+C\) 並不是 \(MAX(C+M,T)\)

我們所求時間為：\(設備->緩沖區->工作區->CPU處理\)

與我們求公式時選定的周期時間：\(MAX(緩沖區->工作區->CPU處理,設備->緩沖區)\)

不一致。

接下來讓我們找一找內在聯系

這里還是以CPU處理結束的結束作為一個數據塊處理完畢的標志。

1. 考慮 (C+M) <T 的情況：

   由上圖2.5可知，在時間段\(0\)~\(3T+M+C\)中共處理了三個數據塊

   \(T_{總}=\) \(T+MAX(M+C,T)+MAX(M+C,T)+M+C\)

   ​ \(= T+2*MAX(M+C,T)+M+C\)

2. 考慮 (C+M) >T 的情況：

   由上圖2.6可知，在時間段\(0\)~\(T+3(M+C)\)中共處理了三個數據塊

   \(T_{總}=\) \(T+MAX(M+C,T)+MAX(M+C,T)+M+C\)

   ​ \(= T+2*MAX(M+C,T)+M+C\)

因此，不論是 (C+M)>T 還是 (C+M)<T ,\(N\)塊數據塊從設備->緩沖區->工作區->cup處理耗時為：\(T+(N-1)*MAX(M+C,T)+M+C\)

\(=T+(N-1)*緩沖區平均處理一塊數據塊的時間+M+C\)

例題

某文件占10個磁盤塊，現要把該文件的磁盤塊逐個讀入主存緩沖區，並送入用戶去進行分析，假設一個緩沖區與一個磁盤塊大小相同，把一個磁盤塊讀入緩沖區的時間為100μs，將緩沖區的數據傳送到用戶區的時間是50μs，CPU對一塊數據進行分析的時間為50μs。在雙緩沖區的結構下，讀入並分析該文件的時間是多少？

甘特圖：

初始狀態為：工作區、緩沖區1、緩沖區2均為空。

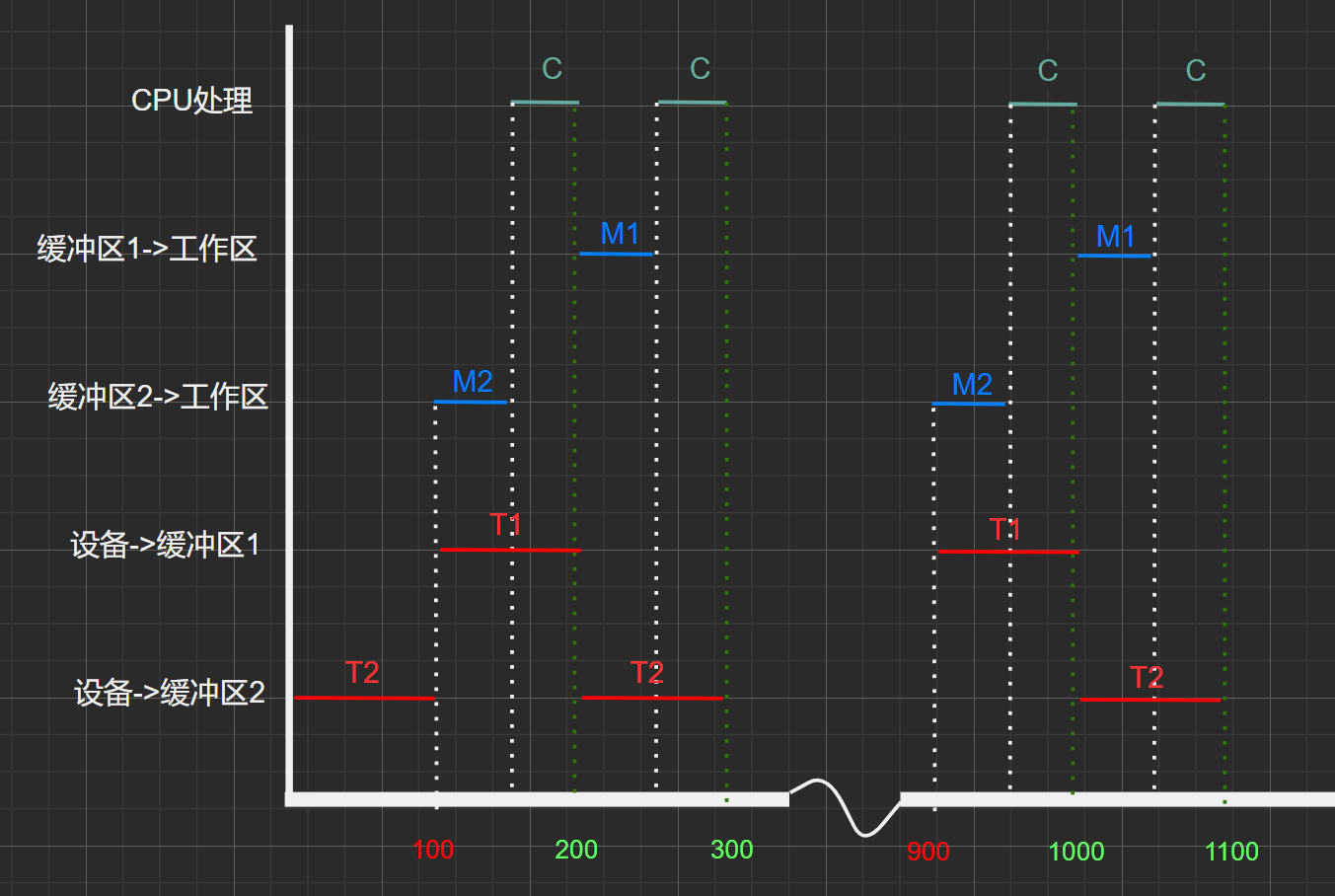
套用公式：
\(T+(N-1)*MAX(M+C,T)+M+C\)

\(=T+(N-1)*緩沖區平均處理一塊數據塊的時間+M+C\)

\(=100μs+(10-1)*MAX[(50+50)μs,100μs]+50+50=1100μs\)