例題:
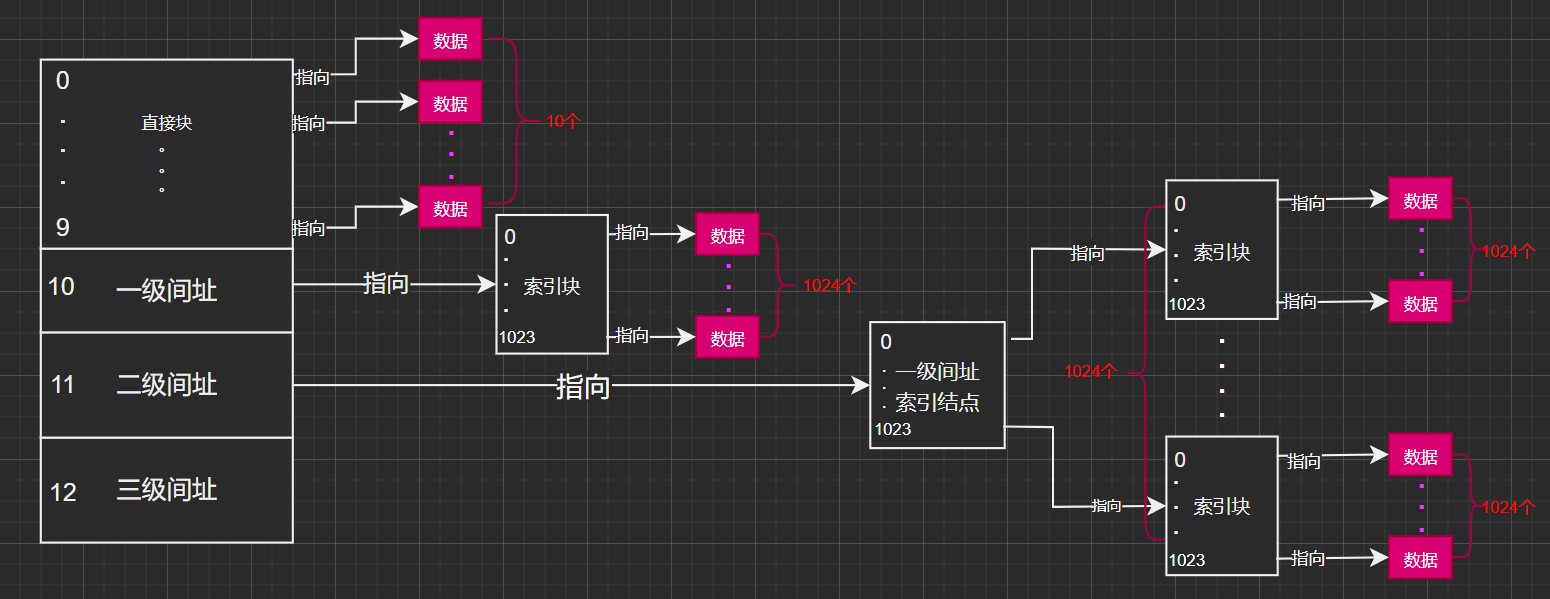
某系統文件采用混合索引的方式組織文件的數據存放,如上圖所示,假定在文件的 \(INode\) 中設有13個地址項,其中直接索引10項,一次間接索引項1項,二次間接索引項1項,三次間接索引項1。數據塊的大小為\(4KB\) ,磁盤地址用\(4B\)表示,試問:
-
這個文件系統允許的最大文件長度是多少?(等價問法 索引能訪問到的地址空間總大小為多大)
-
假設文件目錄存放在磁盤上。FCB占\(64B\),其中文件名占\(8B\) 。若某一目錄文件共有\(1024\)個FCB。
2.1 查找該目錄文件的某個FCB的平均訪問磁盤次數 (注意 只能順序訪問,考慮什么時候為最佳/最壞訪問情況)
2.2 在將FCB分解成兩個部分,第一部分占\(16B\)(包括文件名和文件內部號),第二部分占\(56B\)(包括文 件內部號和文件的其他描述信息)的情況下,求解 2.1
-
若使用文件分配表(FAT)
3.1 對於\(540MB\)的硬盤,其FAT最少需要占用多少存儲空間?
3.2 若FAT的每個表項僅存放數據塊號,占\(2B\),則FAT的最大長度為多少字節?
-
在索引結點已放入內存的情況下,若要讀取一個文件的第\(10000B\) 、\(4G\) 的內容,分別需要訪問磁盤多少次?
-
一個\(4GB\)大小的文件,在這個文件系統中實際占用多少空間?
【解】
-
計算公式:\(所有索引節點指向的數據塊的數目 × 數據塊大小\)
在這里,一個直接塊里存放的指針指向一個數據塊。
- 直接塊指向的數據塊數目:10塊,
(相關考法:當文件不超過多大時,可以只用直接塊。\(直接塊數目*數據塊大小 = 10 * 4KB\))
-
一級間址塊指向一個索引表,該索引表中指向數據塊的指針數目:\(4KB/4B = 1024\)
-
二級間址塊中存放的一級間址塊數目:\(4KB/4B = 1024\) 塊,又因為一個一級間塊能指向1024個數據塊,因此一個二級間塊能指向\((1024)^2\)個數據塊
-
類似的,三級間址塊能指向\((1024)^3\)個數據塊
所有索引節點指向的數據塊數目為:\(M = 10+1024+1024^2+1024^3\)
故最大文件長度為:\(M*4KB\)
-
求解平均訪問目錄文件被裝在不同的磁盤塊的次數
-
1
-
目錄文件總大小:\(M = FCB數目 * 單個FCB大小 = 1024 * 64B\)
-
裝載目錄文件所需的磁盤塊數:\(\lceil M/數據塊大小\rceil\) = \(\lceil(1024*64B)/4KB\rceil = 16\)
[最佳/差情況:所需訪問的FCB位於第一/最后一個磁盤塊]
- 平均訪問16個磁盤查找目錄項的次數:\(\frac {1+2+..+16}{16}=8.5次\)
-
-
2 因為原本整個FCB都是在目錄中的,而分解之后將一部分(\(56B\))放在了目錄之外,因此FCB占用的空間大小只有\(16B\)以便減少目錄的體積,但是這樣也造成了,當檢索完全部目錄項之后還需要額外的一次讀磁盤操作以便找齊完整的FCB
-
目錄文件總大小:\(M = FCB數目 * 16B = 1024 * 16B\)
-
裝載目錄文件所需的磁盤塊數:\(\lceil M/數據塊大小\rceil\) = \(\lceil(1024*16B)/4KB\rceil = 4\)
-
平均訪問4個磁盤查找目錄項的次數:\(t_1=\frac {1+2+..+4}{4}= 2.5次\)
-
查找完全部目錄項之后再查找剩余的FCB信息的平均次數:\(t_2 = \frac {1+1+1+1}4 = 1\)次
因此FCB的平均次數為:\(t_1+t_2 = 2.5+1 = 3.5\)次
-
-
-
1
-
對於\(540MB\)大小的硬盤,硬盤的總塊數為:\(N = 硬盤塊總大小/數據塊大小 = 540MB/4KB\)
-
要用FAT表來表示\(0\) ~\(N\)范圍的硬盤快,則FAT的每個表項的表目需要的位數為:\(\lceil log_2N\rceil\) = \(18\) ,
轉換為字節 => \(18/8 = 2.25B\)
- 又因為有\(N\)個硬盤總塊數,因此FAT有\(N\)個(行)表項。這樣FAT占用的總大小為:\(N*2.25B\)
-
-
2
- \(2B=16bit\),因此FAT表項可以表示的磁盤塊的范圍為:\(0\) ~ \(2^{15}-1\) ,由於磁盤塊與表項一一對應,因此也可以得到表項數目為\(2^{16}\)
- FAT占用的總大小為:\(2^{16} * 2B\)
- \(10000B\)的內容存放在第\(\lceil10000B/4KB\rceil = 10\) (下標號為\(9\))個直接塊中。
通過直接塊中的指針去訪問對應的磁盤,因此只需要訪問磁盤一次即可。
- \(4GB的內容存放所需物理塊數為:4GB/4KB = 2^{20}\)
所用塊 所能表示物理塊范圍最大值 直接塊 10 < \(2^{20}\) 直接塊+一級間址 10 + \({{\frac{4KB}{4B}}^2}\) = 10 + \(2^{10}\) < \(2^{20}\) 直接塊+一級間址+二級間址 10 + \({{\frac{4KB}{4B}}^2}\) + =\({{\frac{4KB}{4B}}^3}\) 10 + \(2^{10}\) +\(2^{20}\) > \(2^{20}\) 因此可以看出,\(4GB\)的內容存放在二級間址下的某個數據塊中,
讀取\(4GB\)的文件需要三次訪問磁盤操作:
第一次從二級間址中獲取一級索引結點表地址,並將其放入內存;第二次,從一級索引結點表中獲取索引塊地址,並將放入內存;第三次,從索引塊中獲取所需訪問的最終文件的地址,並將相應頁面調入內存。
-
該文件實際占用空間大小:\(\lfloor儲存該文件索引塊的大小\rceil + \lfloor該文件大小\rceil\)
-
由題4可知,儲存\(4GB\)大小的文件需要用到直接塊+一級間址+二級間址
-
因此與索引相關占用空間大小的有:\(n1\):13個\(INode\)結點;\(n2\):一級間址所指向的索引塊;\(n3\):二級間址所指向的一級間址索引結點;\(n4\):一級間址索引結點所指向的索引塊;
具體的可看下圖:
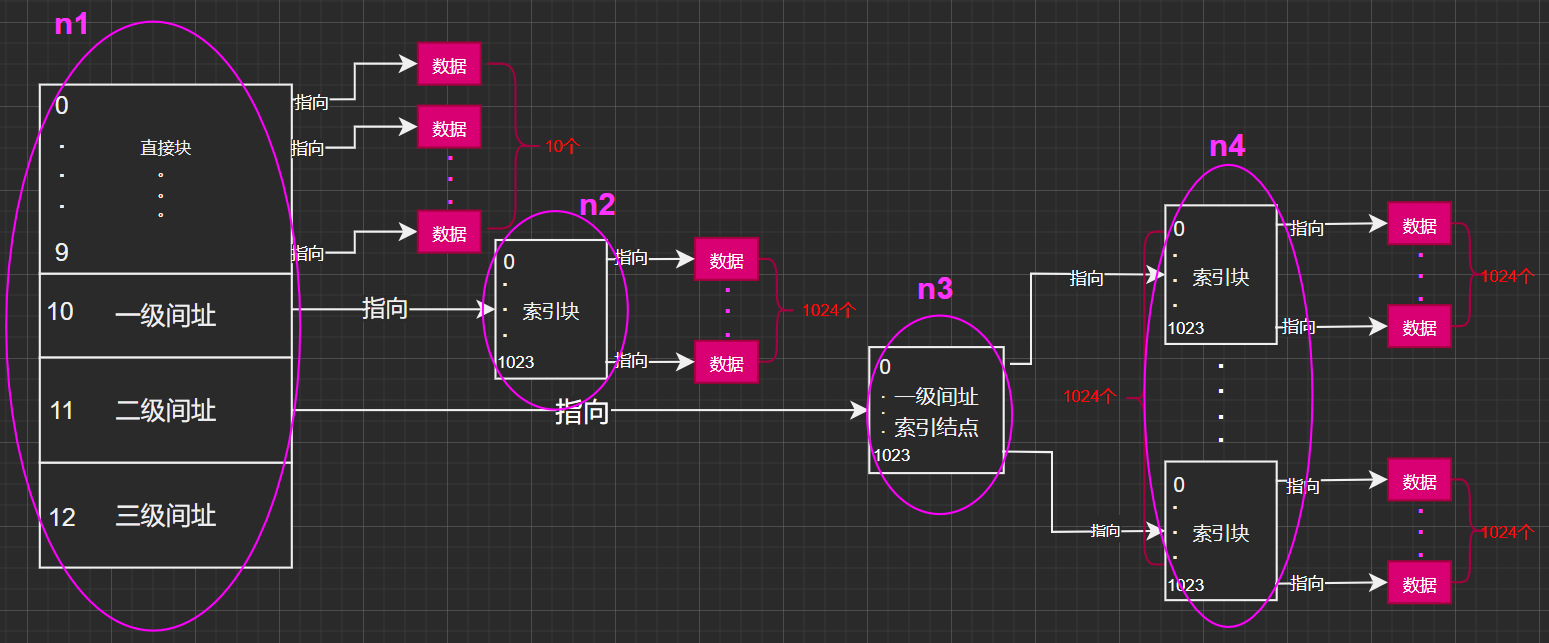
- 其中不難發現,直接塊
(對應INode中的第0~9號塊),與一級間接址(對應INode中的第10號塊)下的全部物理塊都將會被用到。因此,\(n2\)數量為1,\(n3\)數量為1。因此我們所需要求解的只有\(n4\)。
而求解\(n4\)可以利用物理塊數量來進行逆向求解。
- \(4GB的內容存放所需物理塊數為:N = 4GB/4KB = 2^{20}\) (對應上圖中的粉色框框個數)
\(n4 = \lceil \frac{N - 直接塊所表示的物理塊數 - n2索引塊所能表示的物理塊數}{一個索引塊能儲存的地址數}\rceil\)
= \(\lceil \frac{2^{20} - 10 - 1024}{4KB/4B}\rceil\)
≈ 1023
- 由於\(n2、n3、n4\)均以一個物理塊為單位,\(n1\)中的每一個分塊儲存着一個磁盤地址(4B)
此時便可以求得儲存該文件索引塊的大小:
=\((n2+n3+n4)*物理塊大小 + n1*磁盤地址大小\)
=\((1+1+1023)*4KB+13*4B\)
- 因此該文件實際占用空間大小 = \((1+1+1023)*4KB + 13*4B + 4GB\)
-
