分頁儲存
基本概念
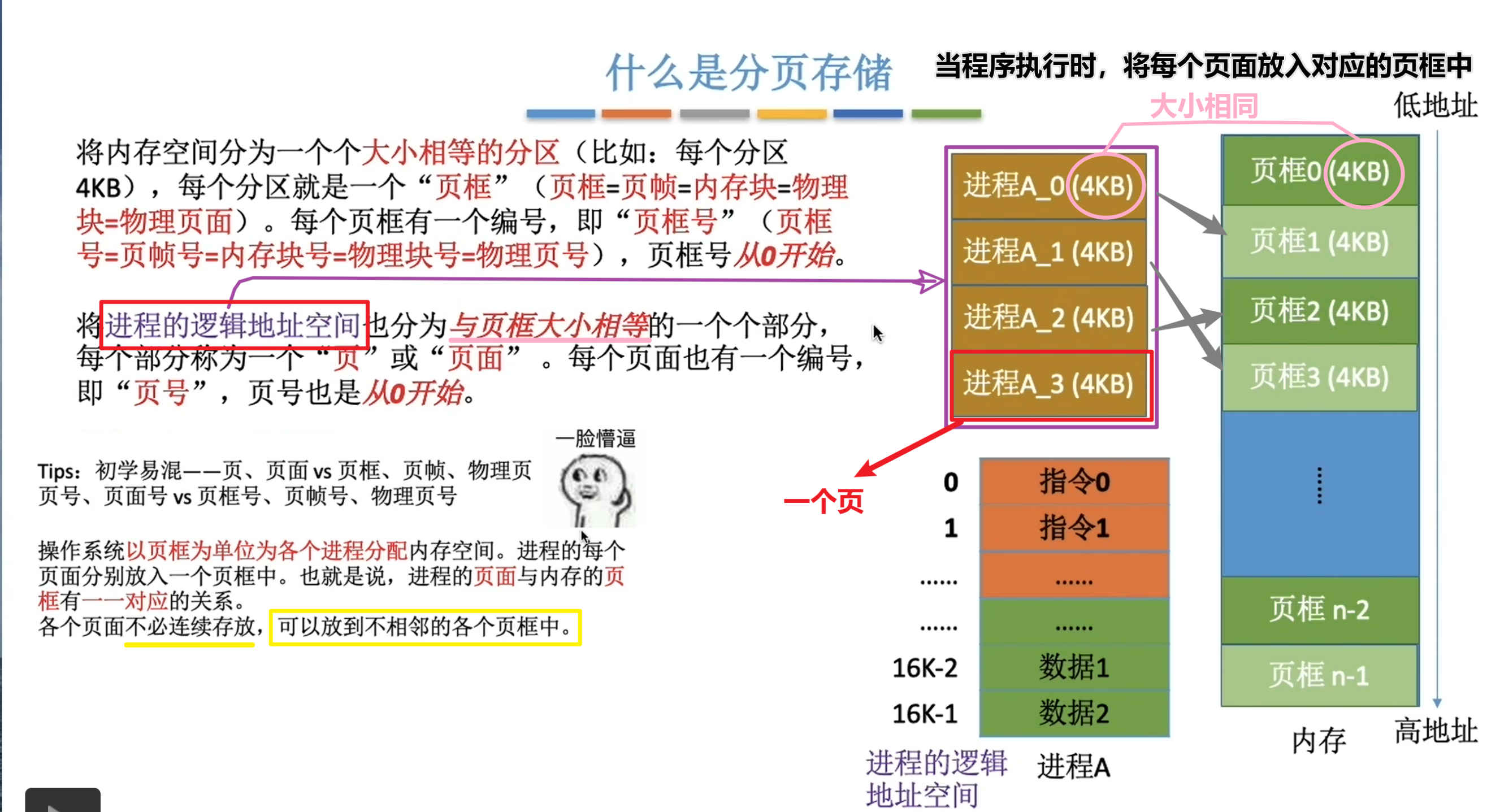
重要數據結構--頁表
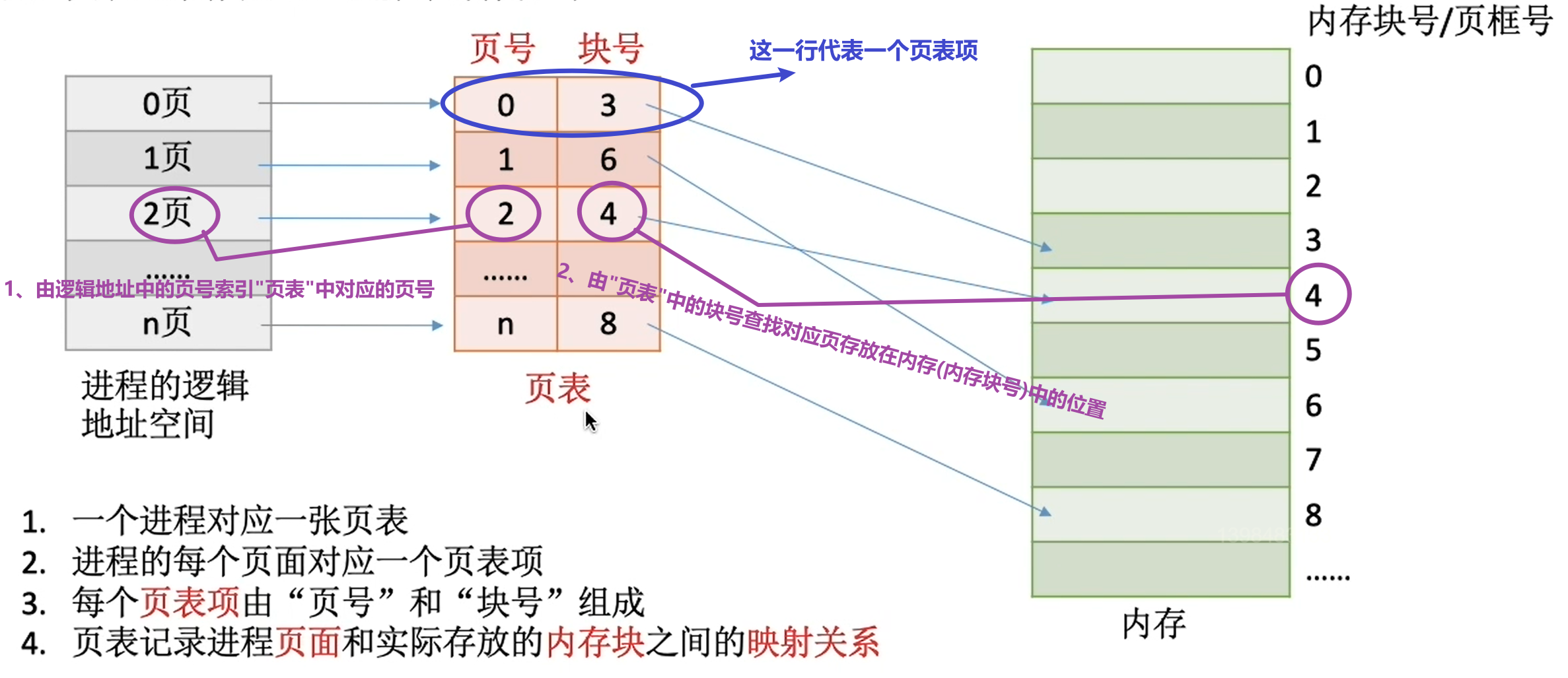
1、每個頁表項占用多少字節?
Eg:假設某系統物理內存大小為\(4GB\),頁面大小為\(4KB\),則每個頁表項至少應該為多少字節?
由題目可知,\(內存塊大小 = 頁面大小 = 4KB = 2^{12}B\)
又因為\(4GB = 2^{32}B\)
所以\(4GB\)的內存總共會被分為\(2^{32}/2^{12}=2^{20}\)個內存塊
所以內存塊號的范圍應該是 \(0\) ~ \(2^{20}-1\)
又因為一位二進制可以表示的狀態有\(2^1\)種
所以全部的內存塊號至少要用\(log_2{2^{20}}=20(位)bit\)來表示
又由於計算機分配內存是以字節(B)為單位分配,因此需要將位(bit)轉化位字節 \(1B = 8bit\)
所以至少需要\(3B\)來表示塊號\((3*8=24bit)\)
又由於頁表項另外一個組成:頁號不占用存儲空間(見下面解釋),
因此一條頁表項的大小只有塊號做貢獻,即\(3B\) ,而上例中整個頁表有\((n+1)\)個頁表項,故存儲整個頁表至少需要\(3*(n+1)B\)
另外,
重要考點:由計算機中內存塊的數量推算出頁表項中塊號至少占用多少字節
由於頁表中的頁表項是連續存放的,因此頁號可以是隱含的,不需要占用空間。可以類比數組,數組在內存中只存放數據,並不會單獨的存放多一個下標號。
1.1、如何根據頁號找到(在內存中)對應的頁表項(的地址)

這里需要注意的一點是,頁表中的塊號所記錄的只是內存塊號,而非內存塊的起始地址。
J號內存塊的起始地址為: J * 內存塊大小
但是當我們將頁表項按照上個例題所給的條件存放在內存時:一個頁面為\(4KB\),一個頁表項大小為\(3B\),則每個頁框可以存放\((4KB)4096B/3B =1365\)(序號從0開始,即存放0~1364號頁表項)個頁表項,但是這個頁表框會剩余 \(4096\%3=1B\)頁內碎片,又由於一個頁表項是連續存放的,不能分開存放在不同的頁框中,所以下一個頁表項第1365只能存放在下一個頁框中,而不能填補上一個頁框的1B頁內碎片。
因此,1365號頁表項存放的地址為:X+3*1365 +1。此時可以看出,由於頁表項之間並沒有連續存放,所以上面的公式X+3*I失效。
但是如果我們將頁表項的占用大小改成4B的話,則每個頁框剛好可以存放1024個頁表項,1024號頁表項雖然是存放在下一個頁框中的,但是它的地址依然可以用\(X+4*1024\) 得出,因為每個頁框都剛好可以被填滿,不存在頁內碎片,即頁表項之間連續存放。
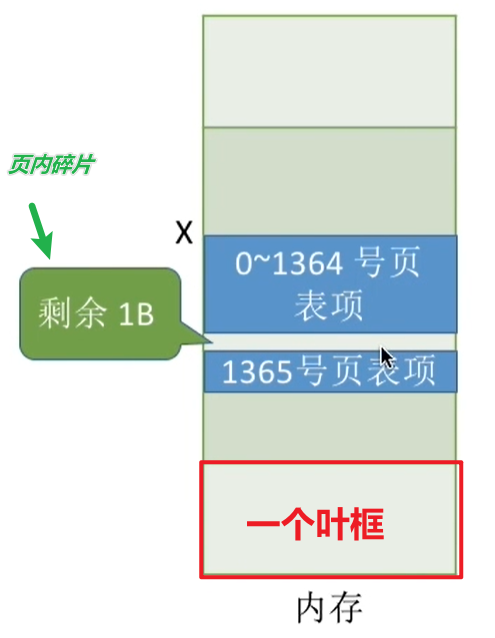
結論:理論上,頁表長度為\(3B\)即可表示內存塊號的范圍,但是,為了方便頁表的查詢,常常會讓一個頁表項占用更多的字節,使得每個頁面恰好可以裝得下整數個頁表項
2、如何實現從邏輯地址到物理地址的轉換
由分頁的特點:用於存放進程的頁框是離散存儲的,但是頁框內部是連續存放的。所以我們可以先找到該頁框的起始地址,然后再加上框內的偏移量即可求得具體的物理地址,具體的:
假如要訪問邏輯地址A,則
- 確定邏輯地址對應的“頁號” P
- 找到P號頁面在內存中的起始地址(需要查頁表,起始地址為: 內存塊號 * 內存塊大小”)
- 確定邏輯地址A的“頁內偏移量”W
- 最后邏輯地址A所對應的物理地址 = P號頁面在內存中的起始地址 + 頁內偏移量W
舉例說明:
如何將 將邏輯地址拆分成頁號與頁內偏移量。
在某計算機系統中,頁面大小是\(50B\)。某進程邏輯地址空間大小為\(200B\),則邏輯地址\(110\)對應的頁號、頁內偏移量是多少?
由題目所給,可以將進程邏輯地址空間分成下圖:

由上圖不能看出:
頁號 = 邏輯地址 / 頁面長度 (取除法的整數部分)
頁內偏移量 = 邏輯地址 % 頁面長度(取除法的余數部分)
因此例子中所給的邏輯地址110
頁號P = 100 / 50 = 2
頁內偏移量W = 100 %50 = 10
因此物理地址為 = \((頁表中P所對應的物理塊號) * 物理塊大小 + W\)
2.1 二進制的邏輯結構的地址划分
在計算機內部,地址是用二進制表示的,如果頁面大小剛好是2的整數冪,則計算機硬件可以很快速的把邏輯地址拆分成(頁號,頁內偏移量)
邏輯地址結構(假設操作系統用32個二進制來表示邏輯地址):
| 31 ................. 12 | 11 ................. 0 |
|---|---|
| 頁號P | 頁內偏移量W |
地址結構包含兩部分:前一部分為頁號P,后一部分位頁內偏移量W。如果每個頁面大小位\(2^kB\),用二進制表示邏輯地址,則末尾k位即為頁內偏移量,其余部分就是頁號。
- 如果由K位表示“頁內偏移量“,則說明系統中一個頁面的大小是2K個內存單元”
- 如果由M位表示“頁號“,則說明系統中,一個進程最多允許有2M個頁面,即,頁號范圍為 :0 ~ 2M-1
如上表中,地址長度為32位,\(0\) ~\(11\)位為“頁內偏移量”,或稱“頁內地址” ,可知頁面大小為:\(2^{12}B\) ;\(12\)~\(32\)為頁號。
因此,可以將十進制的頁號與頁內偏移量單獨的轉換成二進制的表示形式,然后將將其拼接:\(頁號+頁內偏移量\)
舉例說明:
假設某計算機用32個二進制表示邏輯地址,頁面大小為\(4KB = 2^{12}B = 4096B\) (結構划分與上表單一致)

如,邏輯地址\(4097\) 轉化:
頁號 = \(4097 / 4096 = 1\) 轉化為長度占20位的二進制形式為:00000000000000000001
頁內偏移量 = \(4097 \% 4096 = 1\) 轉化為長度占12位的二進制形式位:000000000001
然后將將其拼接得到二進制形式的邏輯地址:\(頁號+頁內偏移量\) = 00000000000000000001000000000001
同理,如果內存塊的大小剛好也是2的整數次冪的話,該方法也適用。

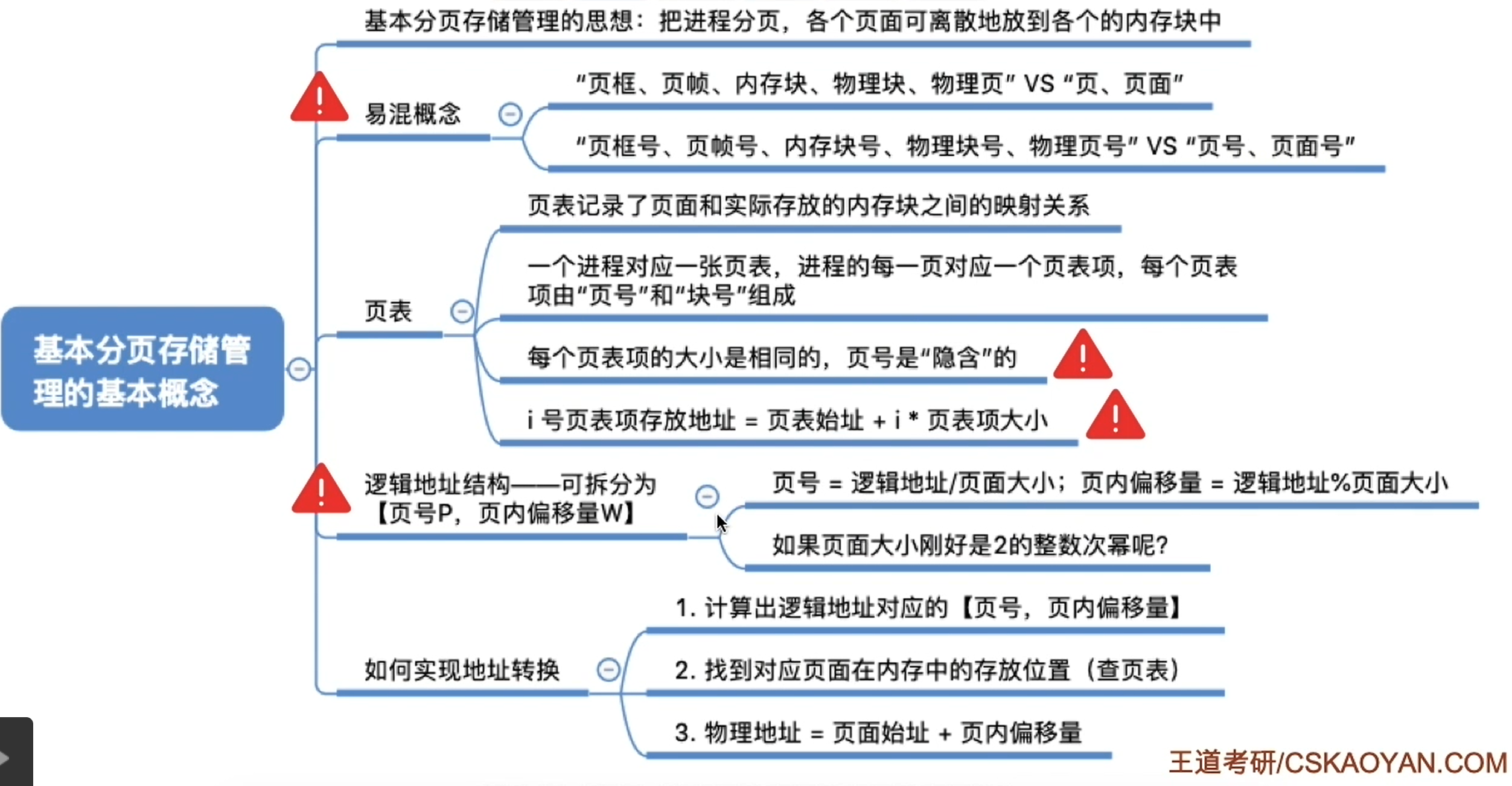
3、總結
兩級頁表
1、單級別頁表存在的問題
由上面的如何根據頁號找到對應的頁表項中可以得知,該方法適用於條件為,所有頁表項必須為連續存放在內存中。
現在考慮這么一個問題:
某計算機系統按字節尋址,支持32位的邏輯地址,采用分頁儲存管理,頁面大小為\(4KB\),頁表長度為\(4B\),則將全部頁表項連續儲存需要多少連續的頁框?
\(4KB=2^{12}B\),然后 \(2^{12}B \%4B=0\),可以看出,頁框大小剛好是頁表項的整數倍,所以頁表項在內存中的存放可以是連續的。另外,頁內地址要用12位表示,剩余20位表示頁號,因此,該系統中一個進程最多有\(2^{20}\)頁,這也是頁表項的數量。而一個頁表項大小位\(4B\),故一個頁表所占的總大小(即全部頁表項的大小總和)為:\(2^{20}*4B = 2^{22}B\) ,將這些頁表項連續分框裝進內存塊時,所需的頁框數量為:\(2^{22}/ 2^{12} = 2^{10}\) ,因此當頁表很大時,需要占用很多個連續的頁框。

1.2、二級頁面表定義
這時我們可以嘗試對頁面進行分頁:
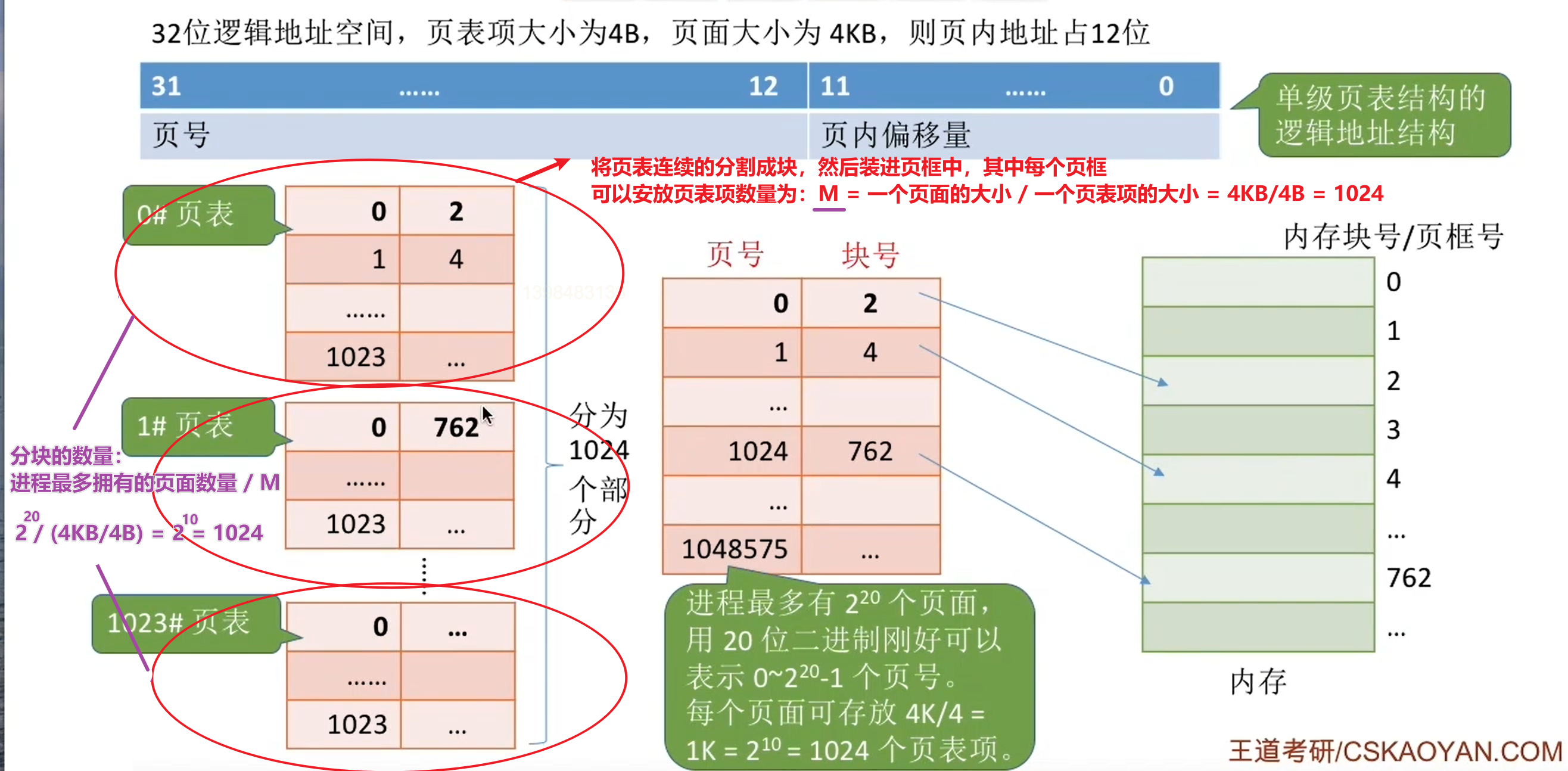
單獨的對頁表的分頁生成一個頁表進行進行映射:頁目錄表
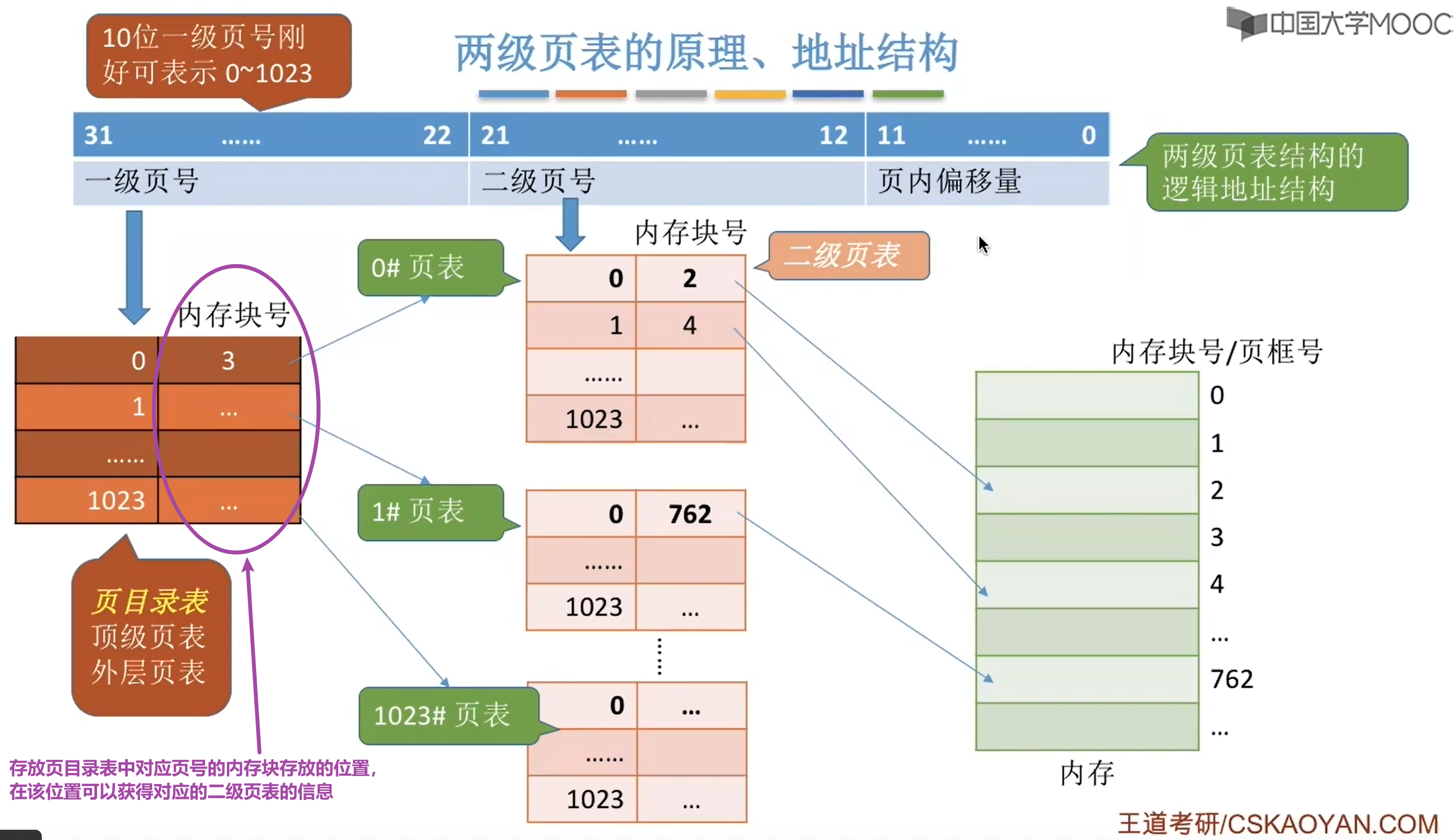
1.3、二級頁表的地址轉換
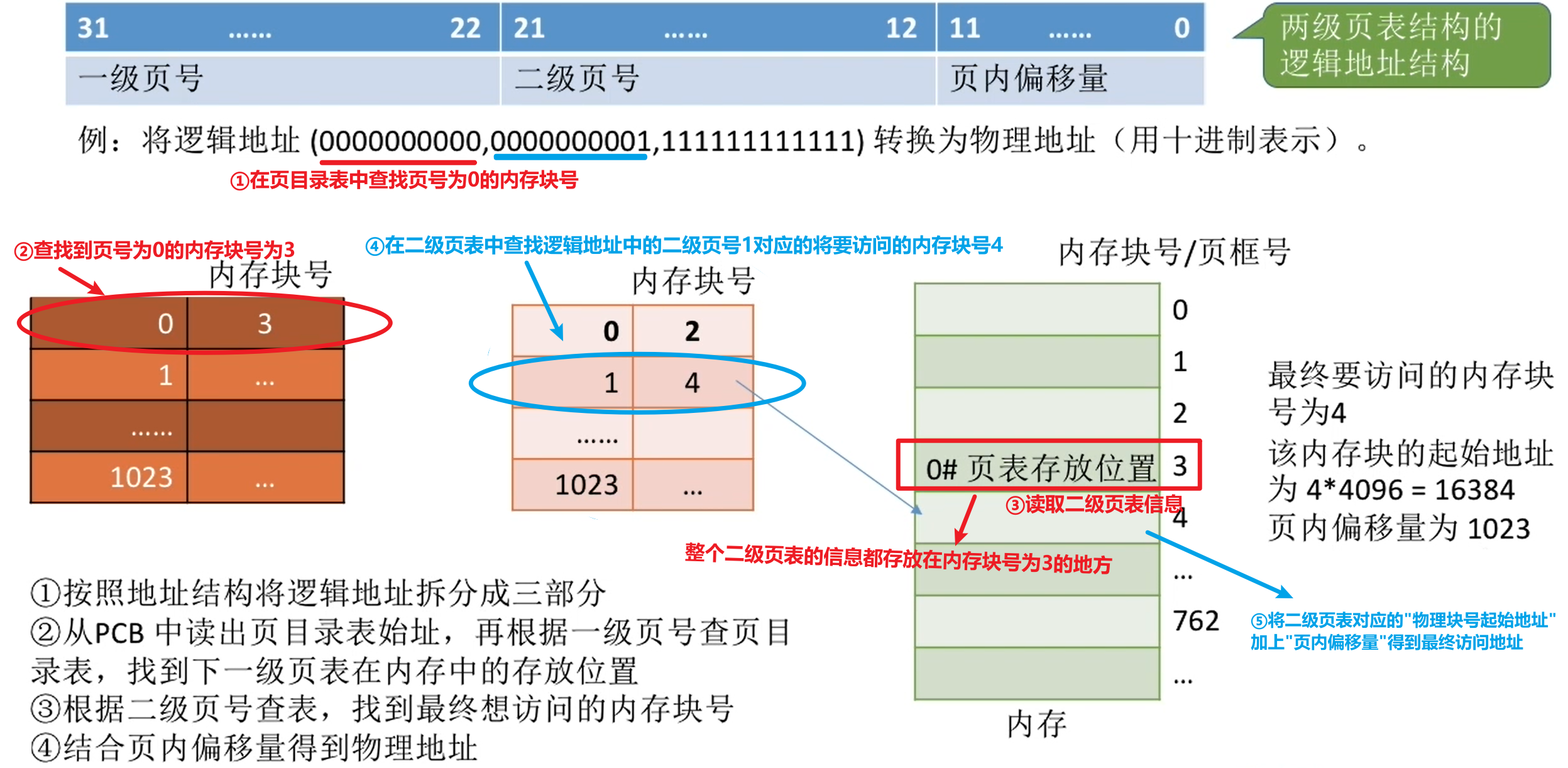
2.1、幾個需要注意的細節
- 若采用多級頁表機制,則各級頁表的大小不能超過一個頁面,

-
兩級頁表的訪存次數分析(假設沒有快表機構)
- 第一次訪存:訪問內存中的頁表目錄表
- 第二次訪存:訪問內存中的二級頁表
- 第三次訪存:訪問目標內存單元
總結:N級頁表的訪存次數為:\(N+1\) 次
3、總結
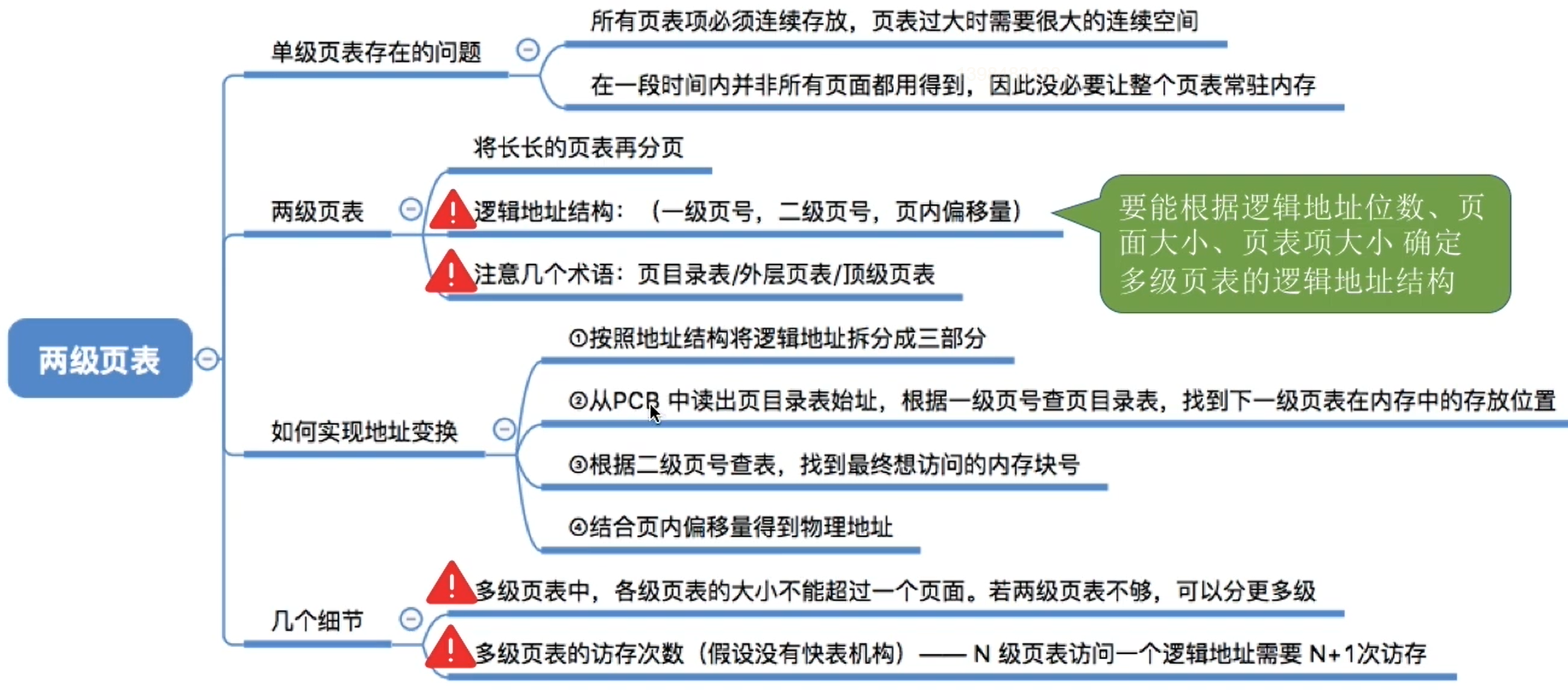
課后例題
-
某計算機主存按字節編址,采用二級分頁儲存管理,地址結構如下:
頁目錄號(10位) 頁號(10位) 頁內偏移量(12位) 則 虛擬地址 \(2050\) \(1225H\) 對應的 頁目錄號、頁號分別是()()
題目給出的邏輯地址是十六進制的,我們需要將其轉化為二進制高位補零,然后將其與地址結構進行對比划分 前10位、11~20位、21~32位分別對應:頁目錄號,頁號,頁內偏移量 <-高位 低位-> 2 0 5 0 1 2 2 5 / \ / \ / \ / \ / \ / \ / \ / \ 0010 0000 0101 0000 0001 0010 0010 0101 |------頁目錄號-----|---------頁號-------| 0010 0000 01 01 0000 0001 對兩個二進制重新從低位開始編排(四個一組): 00 1000 0001 01 0000 0001 高位補零: 0000 1000 0001 0001 0000 0001 頁目錄號 = 0000 1000 0001 頁號 = 0001 0000 0001 -
某計算機主存按字節編址,邏輯地址和物理地址都是32位,頁表項大小為4B。
如果其使用的分頁存儲管理方式,且其地址結構位:
| 頁號(20位) | 頁內偏移量(12位) |
|---|---|
問:一個代碼段的起始邏輯地址為 \(0000\) \(8000H\) ,其長度為\(8KB\) ,被裝載到物理地址從 \(0090\) \(0000H\) 開始的連續主存空間中。頁表從主存中物理地址 \(0020\) \(0000H\) 開始處處連續存放,如下圖(地址大小自下向上遞增)。請計算出該代碼段對應的兩個頁表項的物理地址、這兩個頁表項中的頁框號,以及代碼頁面2的起始物理地址。
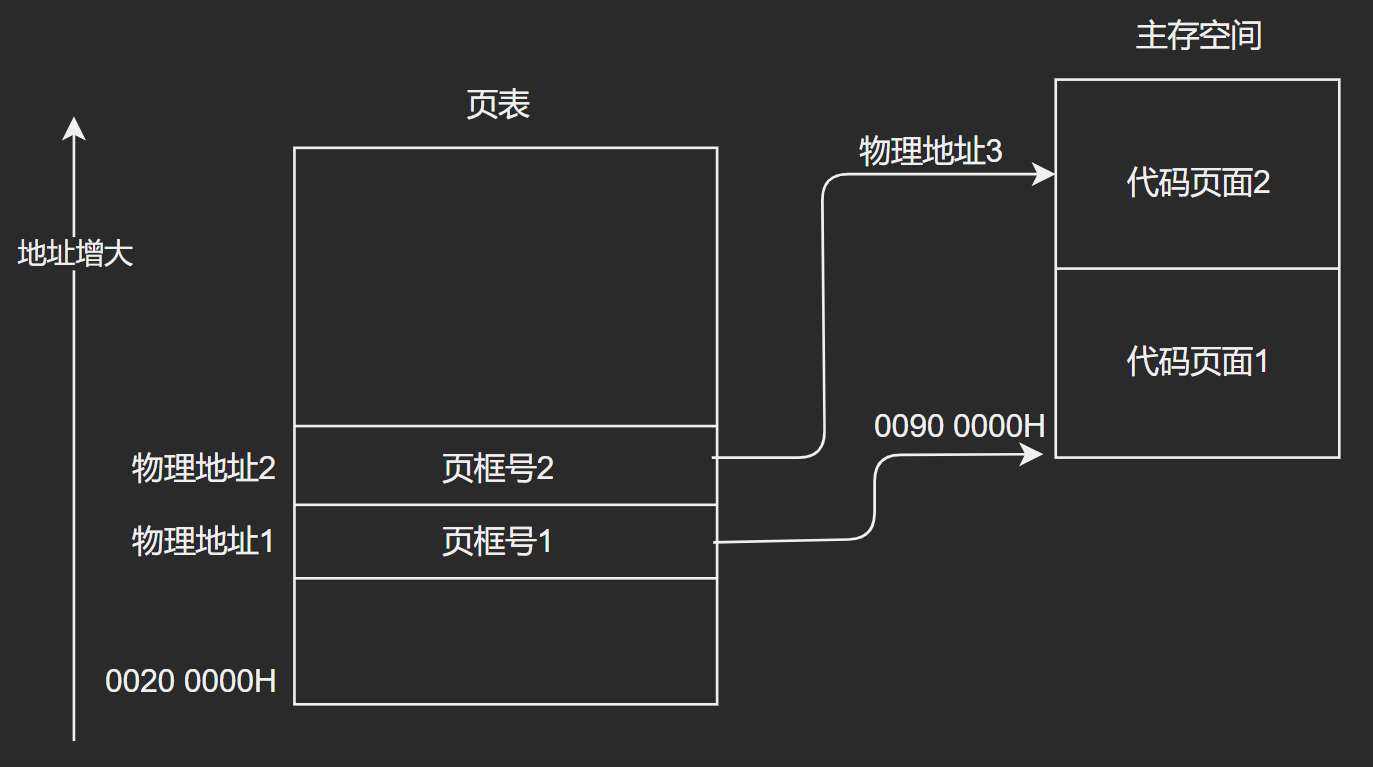
【解】
由邏輯結構可知,前20位為頁號,將代碼段起始邏輯地址轉化為二進制,其前二十位下划線的為頁號:
\(0000\) \(8000H\) = 0000 0000 0000 0000 1000 0000 0000 0000
=> 頁號 = 0000 0000 0000 0000 1000 = 8
因此可得知邏輯代碼段的起始對應頁表的八號頁表 ,於是根據公式I號頁表項的物理地址=頁表始址+I*每個頁表項大小。
=> \(物理地址1 = 八號頁表項物理地址\) = \(0020\) \(0000H\) + \(8*4\) = \(0020\) \(0020H\)
由於兩個相鄰的頁表項地址之間只相差一個頁表項的大小,
=> \(物理地址2 = 物理地址1 + 頁表項大小\) = \(0020\) \(0020H\) \(+4\) = \(0020\) \(0024H\)
由於頁框號對應的是物理塊號,因此我們可以借助用物理塊的物理地址求得的物理塊號從而逆推頁框號。
代碼頁面1所對應的物理塊號為 \(0090 0H\) ,同時也是頁框號1
要求頁框號2,得先求得代碼頁面2的物理地址。
由於兩個相鄰的物理塊地址之間只相差一個頁框大小 (\(2^{12}B\)),
=> \(物理地址3 = 代碼頁面1的物理地址 + 2^{12}\) = $ \(0090\) \(1000H\)
與處理頁框號1步驟相同,可求得頁框號2 = \(0090 1H\)
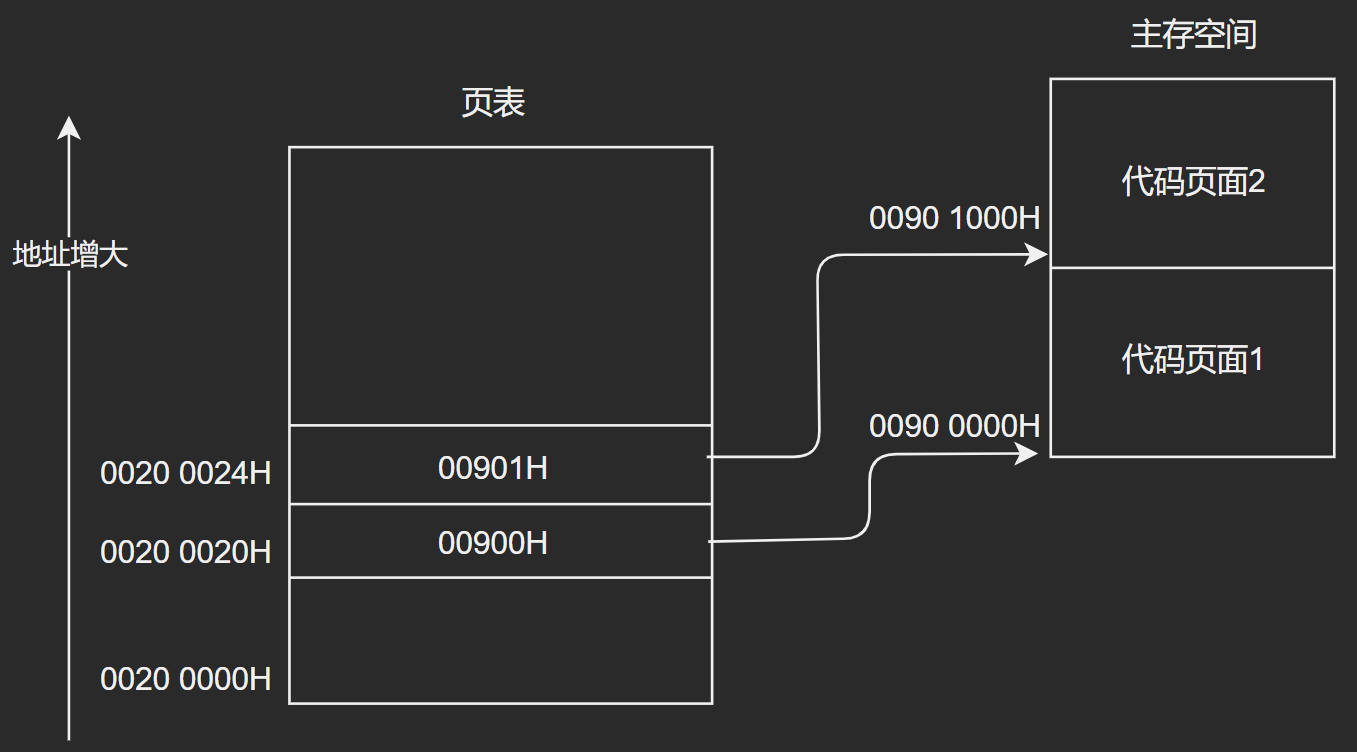
參考:1、22考研·操作系統全程班;2、2021年操作系統考研復習指導
