數據結構——二叉樹

二叉樹

二叉樹的定義

二叉樹在一般的樹上加了兩個限制條件：

• 每個結點最多只有兩個子樹
• 子樹有左右之分，不能顛倒

二叉樹的形態

• 空二叉樹
• 只有根結點
• 只有左子樹，右子樹為空
• 只有右子樹，左子樹為空
• 既有左子樹，又有右子樹

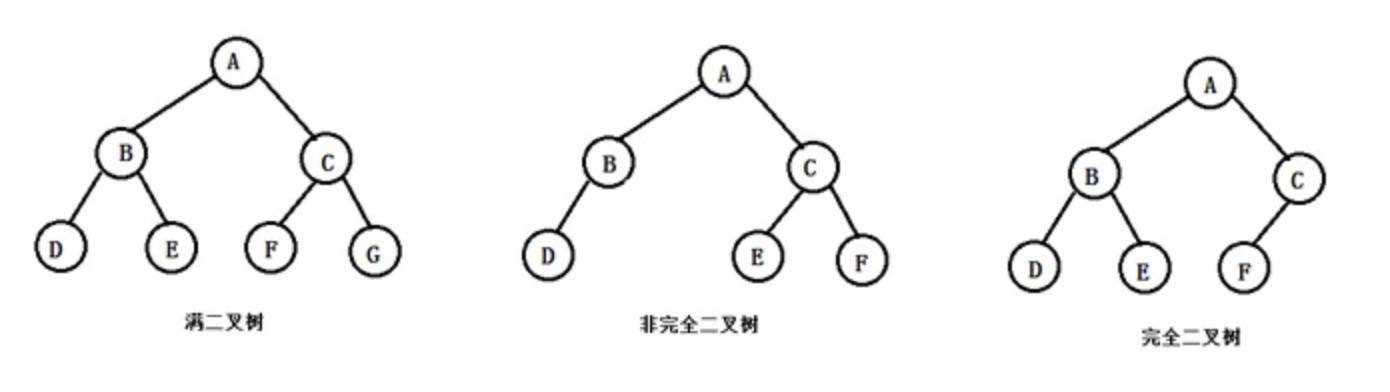
滿二叉樹、完全二叉樹以及非完全二叉樹

• 滿二叉樹：所有的分支結點都有左、右子節點，並且所有葉子結點都集中在最下層的二叉樹。
• 完全二叉樹：對一棵深度為k、有n個結點二叉樹編號后，各節點的編號與深度為k的滿二叉樹相同位置的結點的編號相同，這顆二叉樹就被稱為完全二叉樹
• 非完全二叉樹：沒有滿足完全二叉樹中的條件的二叉樹

二叉樹的主要性質

• 非空二叉樹上葉子結點數等於雙分支結點（有兩個分支的結點）數加1

• 總結點數 = 葉子結點數 + 單分支結點數 + 雙分支結點數 = 單分支結點數 + 2*雙分支結點數

• 總分支數 = 總結點數 - 1 （此性質對所有樹都成立，並非只是二叉樹）

• 空指針數 = 所有結點數 + 1

• 二叉樹第i層最多有2^(i-1)個結點，其中i>=1

• 深度為k的二叉樹最多有2^k - 1個結點

• 有n個結點的完全二叉樹，對各結點從上到下、從左到右編號。若i為某結點a的編號（范圍1~n）。

  • 若i不等於1，則a父結點的編號為不超過(i/2)的最大整數
  • 若2i<=n,則a左兒子的編號為2i; 若2i>n，則a無左兒子
  • 若2i+1<=n,則a的右兒子編號為2i+1;若2i+1>n，則a無右兒子

• 給定n個結點，能構成二叉樹種樹如下
  

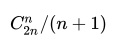
• 具有n個結點的二叉樹深度如下
  

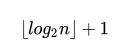
二叉樹的儲存結構

順序儲存結構

順序儲存結構用一個數組來存放一棵二叉樹，這種方式最適合完全二叉樹

定義如下

int Tree[1024];	//順序結構的二叉樹

若某結點編號為i，且存在左兒子和右兒子，則他們分別對應

Tree[i*2];	//左兒子
Tree[2*i+1];	//右兒子

鏈式儲存結構

定義如下

typedef struct _BtTree{
    
    int data;
    struct _BtTree *leftchild;
    struct _BtTree *rightchild;
    
}BtTree;