### 1. 協同過濾算法 協同過濾(Collaborative Filtering)推薦算法是最經典、最常用的推薦算法。 所謂協同過濾, 基本思想是**根據用戶之前的喜好以及其他興趣相近的用戶的選擇來給用戶推薦物品**(基於對用戶歷史行為數據的挖掘發現用戶的喜好偏向, 並預測用戶可能喜好的產品進行推薦),**一般是僅僅基於用戶的行為數據(評價、購買、下載等), 而不依賴於項的任何附加信息(物品自身特征)或者用戶的任何附加信息(年齡, 性別等)**。目前應用比較廣泛的協同過濾算法是基於鄰域的方法, 而這種方法主要有下面兩種算法: * **基於用戶的協同過濾算法(UserCF)**: 給用戶推薦和他興趣相似的其他用戶喜歡的產品 * **基於物品的協同過濾算法(ItemCF)**: 給用戶推薦和他之前喜歡的物品相似的物品 不管是UserCF還是ItemCF算法, 非常重要的步驟之一就是計算用戶和用戶或者物品和物品之間的相似度, 所以下面先整理常用的相似性度量方法, 然后再對每個算法的具體細節進行展開。 <br/> ### 2. 相似性度量方法 1. **傑卡德(Jaccard)相似系數** 這個是衡量兩個集合的相似度一種指標。兩個用戶$u$和$v$交互商品交集的數量占這兩個用戶交互商品並集的數量的比例,稱為兩個集合的傑卡德相似系數,用符號$sim_{uv}$表示,其中$N(u),N(v)$分別表示用戶$u$和用戶$v$交互商品的集合。 $$ sim_{uv}=\frac{|N(u) \cap N(v)|}{\sqrt{|N(u)| \cup|N(v)|}} $$ 由於傑卡德相似系數一般無法反映具體用戶的評分喜好信息, 所以常用來評估用戶是否會對某商品進行打分, 而不是預估用戶會對某商品打多少分。 <br> 2. **余弦相似度** 余弦相似度衡量了兩個向量的夾角,夾角越小越相似。首先從集合的角度描述余弦相似度,相比於Jaccard公式來說就是分母有差異,不是兩個用戶交互商品的並集的數量,而是兩個用戶分別交互的商品數量的乘積,公式如下: $$ sim_{uv}=\frac{|N(u) \cap N(v)|}{\sqrt{|N(u)|\cdot|N(v)|}} $$ 從向量的角度進行描述,令矩陣$A$為用戶-商品交互矩陣(因為是TopN推薦並不需要用戶對物品的評分,只需要知道用戶對商品是否有交互就行),即矩陣的每一行表示一個用戶對所有商品的交互情況,有交互的商品值為1沒有交互的商品值為0,矩陣的列表示所有商品。若用戶和商品數量分別為$m,n$的話,交互矩陣$A$就是一個$m$行$n$列的矩陣。此時用戶的相似度可以表示為(其中$u\cdot v$指的是向量點積): $$ sim_{uv} = cos(u,v) =\frac{u\cdot v}{|u|\cdot |v|} $$ 上述用戶-商品交互矩陣在現實情況下是非常的稀疏了,為了避免存儲這么大的稀疏矩陣,在計算用戶相似度的時候一般會采用集合的方式進行計算。理論上向量之間的相似度計算公式都可以用來計算用戶之間的相似度,但是會根據實際的情況選擇不同的用戶相似度度量方法。 這個在具體實現的時候, 可以使用`cosine_similarity`進行實現: ```python from sklearn.metrics.pairwise import cosine_similarity i = [1, 0, 0, 0] j = [1, 0.5, 0.5, 0] consine_similarity([a, b]) ``` <br> 3. **皮爾遜相關系數** 皮爾遜相關系數的公式與余弦相似度的計算公式非常的類似,首先對於上述的余弦相似度的計算公式寫成求和的形式,其中$r_{ui},r_{vi}$分別表示用戶$u$和用戶$v$對商品$i$是否有交互(或者具體的評分值): $$ sim_{uv} = \frac{\sum_i r_{ui}*r_{vi}}{\sqrt{\sum_i r_{ui}^2}\sqrt{\sum_i r_{vi}^2}} $$ 如下是皮爾遜相關系數計算公式,其中$r_{ui},r_{vi}$分別表示用戶$u$和用戶$v$對商品$i$是否有交互(或者具體的評分值),$\bar r_u, \bar r_v$分別表示用戶$u$和用戶$v$交互的所有商品交互數量或者具體評分的平均值。 $$ sim(u,v)=\frac{\sum_{i\in I}(r_{ui}-\bar r_u)(r_{vi}-\bar r_v)}{\sqrt{\sum_{i\in I }(r_{ui}-\bar r_u)^2}\sqrt{\sum_{i\in I }(r_{vi}-\bar r_v)^2}} $$ 所以相比余弦相似度,皮爾遜相關系數通過使用用戶的平均分對各獨立評分進行修正,減小了用戶評分偏置的影響。具體實現, 我們也是可以調包, 這個計算方式很多, 下面是其中的一種: ```python from scipy.stats import pearsonr i = [1, 0, 0, 0] j = [1, 0.5, 0.5, 0] pearsonr(i, j) ``` 下面是基於用戶協同過濾和基於物品協同過濾的原理講解。 <br> ### 3. 基於用戶的協同過濾 基於用戶的協同過濾(以下用UserCF表示),思想其實比較簡單,**當一個用戶A需要個性化推薦的時候, 我們可以先找到和他有相似興趣的其他用戶, 然后把那些用戶喜歡的, 而用戶A沒有聽說過的物品推薦給A**。 <img src="http://ryluo.oss-cn-chengdu.aliyuncs.com/圖片image-20210629232540289.png" alt="image-20210629232540289" style="zoom: 80%;" /> **UserCF算法主要包括兩個步驟:** 1. 找到和目標用戶興趣相似的集合 2. 找到這個集合中的用戶喜歡的, 且目標用戶沒有聽說過的物品推薦給目標用戶。 上面的兩個步驟中, 第一個步驟里面, 我們會基於前面給出的相似性度量的方法找出與目標用戶興趣相似的用戶, 而第二個步驟里面, 如何基於相似用戶喜歡的物品來對目標用戶進行推薦呢? 這個要依賴於目標用戶對相似用戶喜歡的物品的一個喜好程度, 那么如何衡量這個程度大小呢? 為了更好理解上面的兩個步驟, 下面拿一個具體的例子把兩個步驟具體化。 <br> **以下圖為例,此例將會用於本文各種算法中**  給用戶推薦物品的過程可以**形象化為一個猜測用戶對商品進行打分的任務**,上面表格里面是5個用戶對於5件物品的一個打分情況,就可以理解為用戶對物品的喜歡程度 應用UserCF算法的兩個步驟: 1. 首先根據前面的這些打分情況(或者說已有的用戶向量)計算一下Alice和用戶1, 2, 3, 4的相似程度, 找出與Alice最相似的n個用戶 2. 根據這n個用戶對物品5的評分情況和與Alice的相似程度會猜測出Alice對物品5的評分, 如果評分比較高的話, 就把物品5推薦給用戶Alice, 否則不推薦。 關於第一個步驟, 上面已經給出了計算兩個用戶相似性的方法, 這里不再過多贅述, 這里主要解決第二個問題, 如何產生最終結果的預測。 <br> **最終結果的預測** 根據上面的幾種方法, 我們可以計算出向量之間的相似程度, 也就是可以計算出Alice和其他用戶的相近程度, 這時候我們就可以選出與Alice最相近的前n個用戶, 基於他們對物品5的評價猜測出Alice的打分值, 那么是怎么計算的呢? 這里常用的方式之一是**利用用戶相似度和相似用戶的評價加權平均獲得用戶的評價預測**, 用下面式子表示: $$ R_{\mathrm{u}, \mathrm{p}}=\frac{\sum_{\mathrm{s} \in S}\left(w_{\mathrm{u}, \mathrm{s}} \cdot R_{\mathrm{s}, \mathrm{p}}\right)}{\sum_{\mathrm{s} \in S} w_{\mathrm{u}, \mathrm{s}}} $$ 這個式子里面, 權重$w_{u,s}$是用戶$u$和用戶$s$的相似度, $R_{s,p}$是用戶$s$對物品$p$的評分。 還有一種方式如下, 這種方式考慮的更加前面, 依然是用戶相似度作為權值, 但后面不單純的是其他用戶對物品的評分, 而是**該物品的評分與此用戶的所有評分的差值進行加權平均, 這時候考慮到了有的用戶內心的評分標准不一的情況**, 即有的用戶喜歡打高分, 有的用戶喜歡打低分的情況。 $$ P_{i, j}=\bar{R}_{i}+\frac{\sum_{k=1}^{n}\left(S_{i, k}\left(R_{k, j}-\bar{R}_{k}\right)\right)}{\sum_{k=1}^{n} S_{j, k}} $$ 所以這一種計算方式更為推薦。下面的計算將使用這個方式。 在獲得用戶$u$對不同物品的評價預測后, 最終的推薦列表根據預測評分進行排序得到。 至此,基於用戶的協同過濾算法的推薦過程完成。 根據上面的問題, 下面手算一下: Aim: 猜測Alice對物品5的得分: 1. **計算Alice與其他用戶的相似度(這里使用皮爾遜相關系數)** <img src="http://ryluo.oss-cn-chengdu.aliyuncs.com/JavaCKT9KdW55iLxnNzt.png!thumbnail" alt="img" style="zoom:80%;" /> 這里我們使用皮爾遜相關系數, 也就是Alice與用戶1的相似度是0.85。同樣的方式, 我們就可以計算與其他用戶的相似度, 這里可以使用numpy的相似度函數得到用戶的相似性矩陣: <img src="http://ryluo.oss-cn-chengdu.aliyuncs.com/JavaWJkjP2fHH27Rajrj.png!thumbnail" alt="圖片" style="zoom:80%;" /> 從這里看出, Alice用戶和用戶2,用戶3,用戶4的相似度是0.7,0, -0.79。 所以如果n=2, 找到與Alice最相近的兩個用戶是用戶1, 和Alice的相似度是0.85, 用戶2, 和Alice相似度是0.7 2. **根據相似度用戶計算Alice對物品5的最終得分** 用戶1對物品5的評分是3, 用戶2對物品5的打分是5, 那么根據上面的計算公式, 可以計算出Alice對物品5的最終得分是 $$ P_{Alice, 物品5}=\bar{R}_{Alice}+\frac{\sum_{k=1}^{2}\left(S_{Alice,user k}\left(R_{userk, 物品5}-\bar{R}_{userk}\right)\right)}{\sum_{k=1}^{2} S_{Alice, userk}}=4+\frac{0.85*(3-2.4)+0.7*(5-3.8)}{0.85+0.7}=4.87 $$ 3. **根據用戶評分對用戶進行推薦** 這時候, 我們就得到了Alice對物品5的得分是4.87, 根據Alice的打分對物品排個序從大到小:$$物品1>物品5>物品3=物品4>物品2$$ 這時候,如果要向Alice推薦2款產品的話, 我們就可以推薦物品1和物品5給Alice 至此, 基於用戶的協同過濾算法原理介紹完畢。 <br> ### 4. UserCF編程實現 這里簡單的通過編程實現上面的案例,為后面的大作業做一個熱身, 梳理一下上面的過程其實就是三步: 計算用戶相似性矩陣、得到前n個相似用戶、計算最終得分。 所以我們下面的程序也是分為這三步: 1. **首先, 先把數據表給建立起來** 這里我采用了字典的方式, 之所以沒有用pandas, 是因為上面舉得這個例子其實是個個例, 在真實情況中, 我們知道, 用戶對物品的打分情況並不會這么完整, 會存在大量的空值, 所以矩陣會很稀疏, 這時候用DataFrame, 會有大量的NaN。故這里用字典的形式存儲。 用兩個字典, 第一個字典是物品-用戶的評分映射, 鍵是物品1-5, 用A-E來表示, 每一個值又是一個字典, 表示的是每個用戶對該物品的打分。 第二個字典是用戶-物品的評分映射, 鍵是上面的五個用戶, 用1-5表示, 值是該用戶對每個物品的打分。 ```python # 定義數據集, 也就是那個表格, 注意這里我們采用字典存放數據, 因為實際情況中數據是非常稀疏的, 很少有情況是現在這樣 def loadData(): items={'A': {1: 5, 2: 3, 3: 4, 4: 3, 5: 1}, 'B': {1: 3, 2: 1, 3: 3, 4: 3, 5: 5}, 'C': {1: 4, 2: 2, 3: 4, 4: 1, 5: 5}, 'D': {1: 4, 2: 3, 3: 3, 4: 5, 5: 2}, 'E': {2: 3, 3: 5, 4: 4, 5: 1} } users={1: {'A': 5, 'B': 3, 'C': 4, 'D': 4}, 2: {'A': 3, 'B': 1, 'C': 2, 'D': 3, 'E': 3}, 3: {'A': 4, 'B': 3, 'C': 4, 'D': 3, 'E': 5}, 4: {'A': 3, 'B': 3, 'C': 1, 'D': 5, 'E': 4}, 5: {'A': 1, 'B': 5, 'C': 5, 'D': 2, 'E': 1} } return items,users items, users = loadData() item_df = pd.DataFrame(items).T user_df = pd.DataFrame(users).T ``` <br> 2. **計算用戶相似性矩陣** 這個是一個共現矩陣, 5*5,行代表每個用戶, 列代表每個用戶, 值代表用戶和用戶的相關性,這里的思路是這樣, 因為要求用戶和用戶兩兩的相關性, 所以需要用雙層循環遍歷用戶-物品評分數據, 當不是同一個用戶的時候, 我們要去遍歷物品-用戶評分數據, 在里面去找這兩個用戶同時對該物品評過分的數據放入到這兩個用戶向量中。 因為正常情況下會存在很多的NAN, 即可能用戶並沒有對某個物品進行評分過, 這樣的不能當做用戶向量的一部分, 沒法計算相似性。 還是看代碼吧, 感覺不太好描述: ```python """計算用戶相似性矩陣""" similarity_matrix = pd.DataFrame(np.zeros((len(users), len(users))), index=[1, 2, 3, 4, 5], columns=[1, 2, 3, 4, 5]) # 遍歷每條用戶-物品評分數據 for userID in users: for otheruserId in users: vec_user = [] vec_otheruser = [] if userID != otheruserId: for itemId in items: # 遍歷物品-用戶評分數據 itemRatings = items[itemId] # 這也是個字典 每條數據為所有用戶對當前物品的評分 if userID in itemRatings and otheruserId in itemRatings: # 說明兩個用戶都對該物品評過分 vec_user.append(itemRatings[userID]) vec_otheruser.append(itemRatings[otheruserId]) # 這里可以獲得相似性矩陣(共現矩陣) similarity_matrix[userID][otheruserId] = np.corrcoef(np.array(vec_user), np.array(vec_otheruser))[0][1] #similarity_matrix[userID][otheruserId] = cosine_similarity(np.array(vec_user), np.array(vec_otheruser))[0][1] ``` 這里的similarity_matrix就是我們的用戶相似性矩陣, 長下面這樣:  有了相似性矩陣, 我們就可以得到與Alice最相關的前n個用戶。 <br/> 3. **計算前n個相似的用戶** ```python """計算前n個相似的用戶""" n = 2 similarity_users = similarity_matrix[1].sort_values(ascending=False)[:n].index.tolist() # [2, 3] 也就是用戶1和用戶2 ``` <br/> 4. **計算最終得分** 這里就是上面的那個公式了。 ```python """計算最終得分""" base_score = np.mean(np.array([value for value in users[1].values()])) weighted_scores = 0. corr_values_sum = 0. for user in similarity_users: # [2, 3] corr_value = similarity_matrix[1][user] # 兩個用戶之間的相似性 mean_user_score = np.mean(np.array([value for value in users[user].values()])) # 每個用戶的打分平均值 weighted_scores += corr_value * (users[user]['E']-mean_user_score) # 加權分數 corr_values_sum += corr_value final_scores = base_score + weighted_scores / corr_values_sum print('用戶Alice對物品5的打分: ', final_scores) user_df.loc[1]['E'] = final_scores user_df ``` 結果如下:  至此, 我們就用代碼完成了上面的小例子, 有了這個評分, 我們其實就可以對該用戶做推薦了。 這其實就是微型版的UserCF的工作過程了。 **注意:基於用戶協同過濾的完整代碼參考源代碼文件中的UserCF.py** <br/> ### 5. UserCF優缺點 User-based算法存在兩個重大問題: 1. 數據稀疏性。 一個大型的電子商務推薦系統一般有非常多的物品,用戶可能買的其中不到1%的物品,不同用戶之間買的物品重疊性較低,導致算法無法找到一個用戶的鄰居,即偏好相似的用戶。**這導致UserCF不適用於那些正反饋獲取較困難的應用場景**(如酒店預訂, 大件商品購買等低頻應用) 1. 算法擴展性。 基於用戶的協同過濾需要維護用戶相似度矩陣以便快速的找出Topn相似用戶, 該矩陣的存儲開銷非常大,存儲空間隨着用戶數量的增加而增加,**不適合用戶數據量大的情況使用**。 由於UserCF技術上的兩點缺陷, 導致很多電商平台並沒有采用這種算法, 而是采用了ItemCF算法實現最初的推薦系統。 <br> ### 6. 基於物品的協同過濾 基於物品的協同過濾(ItemCF)的基本思想是預先根據所有用戶的歷史偏好數據計算物品之間的相似性,然后把與用戶喜歡的物品相類似的物品推薦給用戶。比如物品a和c非常相似,因為喜歡a的用戶同時也喜歡c,而用戶A喜歡a,所以把c推薦給用戶A。**ItemCF算法並不利用物品的內容屬性計算物品之間的相似度, 主要通過分析用戶的行為記錄計算物品之間的相似度, 該算法認為, 物品a和物品c具有很大的相似度是因為喜歡物品a的用戶大都喜歡物品c**。 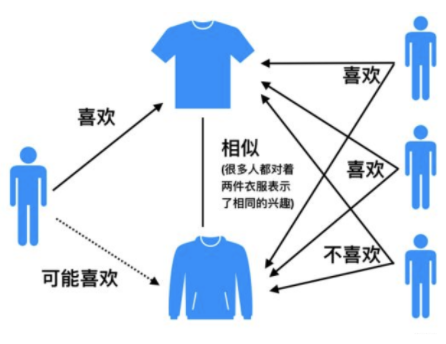 **基於物品的協同過濾算法主要分為兩步:** * 計算物品之間的相似度 * 根據物品的相似度和用戶的歷史行為給用戶生成推薦列表(購買了該商品的用戶也經常購買的其他商品) 基於物品的協同過濾算法和基於用戶的協同過濾算法很像, 所以我們這里直接還是拿上面Alice的那個例子來看。 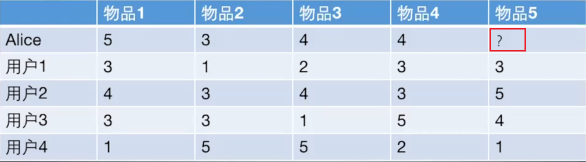 如果想知道Alice對物品5打多少分, 基於物品的協同過濾算法會這么做: 1. 首先計算一下物品5和物品1, 2, 3, 4之間的相似性(它們也是向量的形式, 每一列的值就是它們的向量表示, 因為ItemCF認為物品a和物品c具有很大的相似度是因為喜歡物品a的用戶大都喜歡物品c, 所以就可以基於每個用戶對該物品的打分或者說喜歡程度來向量化物品) 2. 找出與物品5最相近的n個物品 3. 根據Alice對最相近的n個物品的打分去計算對物品5的打分情況 <br> **下面我們就可以具體計算一下, 首先是步驟1:**  由於計算比較麻煩, 這里直接用python計算了: <img src="http://ryluo.oss-cn-chengdu.aliyuncs.com/JavaJOyFti58um61zPsa.png!thumbnail" alt="圖片" style="zoom:80%;" /> 根據皮爾遜相關系數, 可以找到與物品5最相似的2個物品是item1和item4(n=2), 下面基於上面的公式計算最終得分: $$ P_{Alice, 物品5}=\bar{R}_{物品5}+\frac{\sum_{k=1}^{2}\left(S_{物品5,物品 k}\left(R_{Alice, 物品k}-\bar{R}_{物品k}\right)\right)}{\sum_{k=1}^{2} S_{物品k, 物品5}}=\frac{13}{4}+\frac{0.97*(5-3.2)+0.58*(4-3.4)}{0.97+0.58}=4.6 $$ 這時候依然可以向Alice推薦物品5。下面也是簡單編程實現一下, 和上面的差不多: ```python """計算物品的相似矩陣""" similarity_matrix = pd.DataFrame(np.ones((len(items), len(items))), index=['A', 'B', 'C', 'D', 'E'], columns=['A', 'B', 'C', 'D', 'E']) # 遍歷每條物品-用戶評分數據 for itemId in items: for otheritemId in items: vec_item = [] # 定義列表, 保存當前兩個物品的向量值 vec_otheritem = [] #userRagingPairCount = 0 # 兩件物品均評過分的用戶數 if itemId != otheritemId: # 物品不同 for userId in users: # 遍歷用戶-物品評分數據 userRatings = users[userId] # 每條數據為該用戶對所有物品的評分, 這也是個字典 if itemId in userRatings and otheritemId in userRatings: # 用戶對這兩個物品都評過分 #userRagingPairCount += 1 vec_item.append(userRatings[itemId]) vec_otheritem.append(userRatings[otheritemId]) # 這里可以獲得相似性矩陣(共現矩陣) similarity_matrix[itemId][otheritemId] = np.corrcoef(np.array(vec_item), np.array(vec_otheritem))[0][1] #similarity_matrix[itemId][otheritemId] = cosine_similarity(np.array(vec_item), np.array(vec_otheritem))[0][1] ``` 這里就是物品的相似度矩陣了, 大概長下面這個樣子: 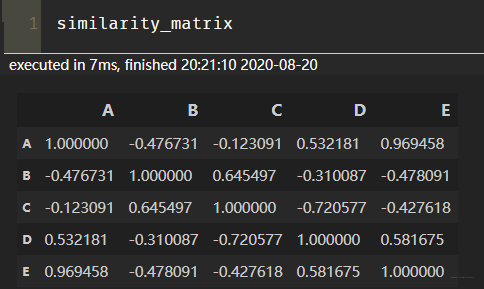 **然后也是得到與物品5相似的前n個物品, 計算出最終得分來。** ```python """得到與物品5相似的前n個物品""" n = 2 similarity_items = similarity_matrix['E'].sort_values(ascending=False)[:n].index.tolist() # ['A', 'D'] """計算最終得分""" base_score = np.mean(np.array([value for value in items['E'].values()])) weighted_scores = 0. corr_values_sum = 0. for item in similarity_items: # ['A', 'D'] corr_value = similarity_matrix['E'][item] # 兩個物品之間的相似性 mean_item_score = np.mean(np.array([value for value in items[item].values()])) # 每個物品的打分平均值 weighted_scores += corr_value * (users[1][item]-mean_item_score) # 加權分數 corr_values_sum += corr_value final_scores = base_score + weighted_scores / corr_values_sum print('用戶Alice對物品5的打分: ', final_scores) user_df.loc[1]['E'] = final_scores user_df ``` 結果如下:  **注意:基於商品的協同過濾算法的完整代碼參考源代碼文件中的ItemCF.py** <br> ### 7. 算法評估 由於UserCF和ItemCF結果評估部分是共性知識點, 所以在這里統一標識。 這里介紹評測指標: 1. 召回率 對用戶u推薦N個物品記為$R(u)$, 令用戶u在測試集上喜歡的物品集合為$T(u)$, 那么召回率定義為: $$ \operatorname{Recall}=\frac{\sum_{u}|R(u) \cap T(u)|}{\sum_{u}|T(u)|} $$ 這個意思就是說, 在用戶真實購買或者看過的影片里面, 我模型真正預測出了多少, 這個考察的是模型推薦的一個全面性。 2. 准確率 准確率定義為: $$ \operatorname{Precision}=\frac{\sum_{u} \mid R(u) \cap T(u)|}{\sum_{u}|R(u)|} $$ 這個意思再說, 在我推薦的所有物品中, 用戶真正看的有多少, 這個考察的是我模型推薦的一個准確性。 為了提高准確率, 模型需要把非常有把握的才對用戶進行推薦, 所以這時候就減少了推薦的數量, 而這往往就損失了全面性, 真正預測出來的會非常少,所以實際應用中應該綜合考慮兩者的平衡。 3. 覆蓋率 覆蓋率反映了推薦算法發掘長尾的能力, 覆蓋率越高, 說明推薦算法越能將長尾中的物品推薦給用戶。 $$ \text { Coverage }=\frac{\left|\bigcup_{u \in U} R(u)\right|}{|I|} $$ 4. 該覆蓋率表示最終的推薦列表中包含多大比例的物品。如果所有物品都被給推薦給至少一個用戶, 那么覆蓋率是100%。 5. 新穎度 用推薦列表中物品的平均流行度度量推薦結果的新穎度。 如果推薦出的物品都很熱門, 說明推薦的新穎度較低。 由於物品的流行度分布呈長尾分布, 所以為了流行度的平均值更加穩定, 在計算平均流行度時對每個物品的流行度取對數。 <br> ### 8. 協同過濾算法的權重改進 <img src="http://ryluo.oss-cn-chengdu.aliyuncs.com/Javaimage-20200923122142218.png" alt="image-20200923122142218" style="zoom:67%;" /> * 基礎算法 圖1為最簡單的計算物品相關度的公式, 分子為同時喜好itemi和itemj的用戶數 * 對熱門物品的懲罰 圖1存在一個問題, 如果 item-j 是很熱門的商品,導致很多喜歡 item-i 的用戶都喜歡 item-j,這時 $w_{ij}$ 就會非常大。同樣,幾乎所有的物品都和 item-j 的相關度非常高,這顯然是不合理的。所以圖2中分母通過引入 $N(j)$ 來對 item-j 的熱度進行懲罰。如果物品很熱門, 那么$N(j)$就會越大, 對應的權重就會變小。 * 對熱門物品的進一步懲罰 如果 item-j 極度熱門,上面的算法還是不夠的。舉個例子,《Harry Potter》非常火,買任何一本書的人都會購買它,即使通過圖2的方法對它進行了懲罰,但是《Harry Potter》仍然會獲得很高的相似度。這就是推薦系統領域著名的 Harry Potter Problem。<br>如果需要進一步對熱門物品懲罰,可以繼續修改公式為如圖3所示,通過調節參數 $α$,$α $越大,懲罰力度越大,熱門物品的相似度越低,整體結果的平均熱門程度越低。 * 對活躍用戶的懲罰 同樣的,Item-based CF 也需要考慮活躍用戶(即一個活躍用戶(專門做刷單)可能買了非常多的物品)的影響,活躍用戶對物品相似度的貢獻應該小於不活躍用戶。圖4為集合了該權重的算法。 <br> ### 9. 協同過濾算法的問題分析 協同過濾算法存在的問題之一就是**泛化能力弱**, 即協同過濾無法將兩個物品相似的信息推廣到其他物品的相似性上。 導致的問題是**熱門物品具有很強的頭部效應, 容易跟大量物品產生相似, 而尾部物品由於特征向量稀疏, 導致很少被推薦**。 比如下面這個例子:  A, B, C, D是物品, 看右邊的物品共現矩陣, 可以發現物品D與A、B、C的相似度比較大, 所以很有可能將D推薦給用過A、B、C的用戶。 但是物品D與其他物品相似的原因是因為D是一件熱門商品, 系統無法找出A、B、C之間相似性的原因是其特征太稀疏, 缺乏相似性計算的直接數據。 所以這就是協同過濾的天然缺陷:**推薦系統頭部效應明顯, 處理稀疏向量的能力弱**。 為了解決這個問題, 同時增加模型的泛化能力,2006年,**矩陣分解技術(Matrix Factorization,MF**)被提出, 該方法在協同過濾共現矩陣的基礎上, 使用更稠密的隱向量表示用戶和物品, 挖掘用戶和物品的隱含興趣和隱含特征, 在一定程度上彌補協同過濾模型處理稀疏矩陣能力不足的問題。 具體細節等后面整理, 這里先鋪墊一下。 <br> ### 10. 課后思考 1.**什么時候使用UserCF,什么時候使用ItemCF?為什么?** 答案: > 1. UserCF > 由於是基於用戶相似度進行推薦, 所以具備更強的社交特性, 這樣的特點非常適於**用戶少, 物品多, 時效性較強的場合**, 比如新聞推薦場景, 因為新聞本身興趣點分散, 相比用戶對不同新聞的興趣偏好, 新聞的及時性,熱點性往往更加重要, 所以正好適用於發現熱點,跟蹤熱點的趨勢。 另外還具有推薦新信息的能力, 更有可能發現驚喜, 因為看的是人與人的相似性, 推出來的結果可能更有驚喜,可以發現用戶潛在但自己尚未察覺的興趣愛好。 > > 對於用戶較少, 要求時效性較強的場合, 就可以考慮UserCF。 > > 2. ItemCF > 這個更適用於興趣變化較為穩定的應用, 更接近於個性化的推薦, 適合**物品少,用戶多,用戶興趣固定持久, 物品更新速度不是太快的場合**, 比如推薦藝術品, 音樂, 電影。 > 下面是UserCF和ItemCF的優缺點對比: (來自項亮推薦系統實踐) 2.**協同過濾在計算上有什么缺點?有什么比較好的思路可以解決(緩解)?** 答案: > **較差的稀疏向量處理能力** > > 第一個問題就是**泛化能力弱**, 即協同過濾無法將兩個物品相似的信息推廣到其他物品的相似性上。 導致的問題是**熱門物品具有很強的頭部效應, 容易跟大量物品產生相似, 而尾部物品由於特征向量稀疏, 導致很少被推薦**。 比如下面這個例子: > >  > > A, B, C, D是物品, 看右邊的物品共現矩陣, 可以發現物品D與A、B、C的相似度比較大, 所以很有可能將D推薦給用過A、B、C的用戶。 但是物品D與其他物品相似的原因是因為D是一件熱門商品, 系統無法找出A、B、C之間相似性的原因是其特征太稀疏, 缺乏相似性計算的直接數據。 所以這就是協同過濾的天然缺陷:**推薦系統頭部效應明顯, 處理稀疏向量的能力弱**。 > > 為了解決這個問題, 同時增加模型的泛化能力,2006年,**矩陣分解技術(Matrix Factorization,MF**)被提出, 該方法在協同過濾共現矩陣的基礎上, 使用更稠密的隱向量表示用戶和物品, 挖掘用戶和物品的隱含興趣和隱含特征, 在一定程度上彌補協同過濾模型處理稀疏矩陣能力不足的問題。 具體細節等后面整理, 這里先鋪墊一下。 **3.上面介紹的相似度計算方法有什么優劣之處?** > cosine相似度還是比較常用的, 一般效果也不會太差, 但是對於評分數據不規范的時候, 也就是說, 存在有的用戶喜歡打高分, 有的用戶喜歡打低分情況的時候,有的用戶喜歡亂打分的情況, 這時候consine相似度算出來的結果可能就不是那么准確了, 比如下面這種情況: > > > >這時候, 如果用余弦相似度進行計算, 會發現用戶d和用戶f比較相似, 而實際上, 如果看這個商品喜好的一個趨勢的話, 其實d和e比較相近, 只不過e比較喜歡打低分, d比較喜歡打高分。 所以對於這種用戶評分偏置的情況, 余弦相似度就不是那么好了, 可以考慮使用下面的皮爾遜相關系數。 4.**協同過濾還存在其他什么缺陷?有什么比較好的思路可以解決(緩解)?** 答案: > 協同過濾的特點就是完全沒有利用到物品本身或者是用戶自身的屬性, 僅僅利用了用戶與物品的交互信息就可以實現推薦,比較簡單高效, 但這也是它的一個短板所在, 由於無法有效的引入用戶年齡, 性別,商品描述,商品分類,當前時間,地點等一系列用戶特征、物品特征和上下文特征, 這就造成了有效信息的遺漏,不能充分利用其它特征數據。 > > 為了解決這個問題, 在推薦模型中引用更多的特征,**推薦系統慢慢的從以協同過濾為核心到了以邏輯回歸模型為核心**, 提出了能夠綜合不同類型特征的機器學習模型。 > > 演化圖左邊的時間線梳理完畢: > >