一、線性回歸
1.定義
線性回歸是利用數理統計中回歸分析,來確定兩種或兩種以上變量間相互依賴的定量關系的一種統計分析方法,運用十分廣泛。其表達形式為y =
w’x+e,e為誤差服從均值為0的正態分布。
回歸分析中,只包括一個自變量和一個因變量,且二者的關系可用一條直線近似表示,這種回歸分析稱為一元線性回歸分析。如果回歸分析中包括兩個或兩個以上的自變量,且因變量和自變量之間是線性關系,則稱為多元線性回歸分析。
2.操作
(1)准備數據

本文介紹的是簡單的一元線性回歸。准備好數據之后,一定要分清楚自變量和因變量。樣本數據中很明顯銷售量屬於自變量,而銷售額屬於因變量。
(2)繪制散點圖

繪制散點圖的目的是先大致觀察一下這兩個變量之間是否存在線性相關性,正相關還是負相關。很明顯,銷售量和銷售額具有線性正相關性。
(3)預測結果
當老板問你:“小樣兒,如果這個月的銷售量是80,根據以往經驗看,銷售額能達到多少啊?”

FORECAST——這個函數可以用於通過一條線性回歸擬合線返回一個預測值。
語法如下:
第一個參數為預測值,第二個參數為因變量的值,第三個參數為自變量的值。 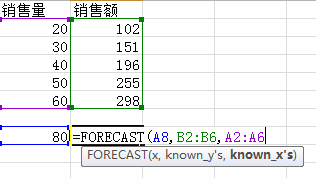

二、相關系數
1.定義
相關系數是最早由統計學家卡爾·皮爾遜設計的統計指標,是研究變量之間線性相關程度的量,一般用字母 r
表示。由於研究對象的不同,相關系數有多種定義方式,較為常用的是皮爾遜相關系數。
在實際工作過程中,主要研究兩個對象之間是否具有線性相關性,以及相關程度有很大。比如,購買奶粉的顧客是否也會購買尿不濕,這兩者之間的關聯度有多大?就可以計算出兩者的相關系數大小從而得出結論。
2.操作
(1)准備數據

(2)繪制散點圖

注意:配圖有點問題,應該為散點圖!!主要是數據是編的,大家理解原理即可!繪制散點圖的目的是初步定性的分析一下,兩者是否具有相關性。
(3)相關系數

CORREL——這個函數可以用來返回兩組數值的相關系數。
語法如下:
第一個參數為計算相關系數的對象1的值,第二個參數為計算相關系數的對象2的值。 
結果顯示,兩者的相關系數為0.648,可以認定兩者存在相關性(r>0.6),一般大於0.6可認為兩者屬於強相關。進一步說明,買奶粉的顧客中買尿不濕的顧客也很多(反過來也可以解釋),可以指導實際零售商進行商品的擺放等操作。


