重新復習藍書(基礎算法,數論,DP和圖論),爭取 \(1.5\) 個月內完成,期間會不定期更新
此次記錄,過往的題也會重新編寫題解並收錄
補題鏈接:Here
0x00 基本算法
0x01 位運算
A題:a^b
https://ac.nowcoder.com/acm/contest/996/A
題目描述
求 a 的 b 次方對 p 取模的值,其中 0 <= a,b,p <= 10^9
輸入描述:
三個用空格隔開的整數a,b和p。
輸出描述:
一個整數,表示a^b mod p的值。
實例:
輸入: 2 3 9
輸出: 8
思路:
這道題是要先算出a的b次冪再對其結果進行求模(取余),因為b最大可為1e+9,按普通做法來做時間復雜度就太大了,顯然這樣過不了題,
能快速算a的b次冪,就能減小時間復雜度,快速冪就是一種不錯的方法。
什么是快速冪:
快速冪是一種簡化運算底數的n次冪的算法,理論上其時間復雜度為 O(log₂N),而一般的朴素算法則需要O(N)的時間復雜度。簡單來說快速冪其實就是抽取了指數中的2的n次冪,將其轉換為時間復雜度為O(1)的二進制移位運算,所以相應地,時間復雜度降低為O(log₂N)。
代碼原理:
以 \(a^{13}\) 為例,
先把指數13化為二進制就是1101,把二進制數字1101直觀地表現為十進制則是如下的等式:
這樣一來 \(a^{13}\) 可以如下算出:
完整AC代碼如下:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;//將long long類型取個別名:ll類型,為了方便
int power(int a, int b, int mod) {
ll ans = 1 % mod;
for (; b; b >>= 1) {
if (b & 1) ans = ans * a % mod;
a = (ll)a * a % mod;//顯式轉化為ll類型進行高精度計算,再隱式轉化為int
}
return ans;
}
int main() {
//freopen("in.txt", "r", stdin);
ios::sync_with_stdio(false), cin.tie(0);
int a, b, mod;
cin >> a >> b >> mod;
cout << power(a, b, mod) << endl;
}
B題:Raising Modulo Numbers
與上面A題寫法一樣
typedef long long ll;
int _;
// 稍微優化下上方代碼:update 21/01/28
ll qpow(ll a, ll b, ll mod) {
ll ans = 1;
a %= mod;
for (; b; a = a * a % mod, b >>= 1)
if (b & 1) ans = ans * a % mod;
return ans;
}
int main() {
// freopen("in.txt", "r", stdin);
ios_base::sync_with_stdio(false), cin.tie(0);
ll M, N;
for (cin >> _; _--;) {
cin >> M >> N;
ll a, b, ans = 0;
while (N--) {
cin >> a >> b;
ans = (ans + qpow(a, b, M)) % M;
}
cout << ans << endl;
}
}
C題:64位整數乘法
鏈接:https://ac.nowcoder.com/acm/contest/996/C
思路:
類似快速冪的思想,把整數b用二進制表示,即
typedef long long ll;
int main() {
//freopen("in.txt", "r", stdin);
ios::sync_with_stdio(false), cin.tie(0);
ll a, b, p; cin >> a >> b >> p;
ll ans = 0;
for (; b; b >>= 1) {
if (b & 1)ans = (ans + a) % p;
a = (a << 1) % p;
}
cout << ans << endl;
}
⭐D題:最短Hamilton路徑
鏈接:https://ac.nowcoder.com/acm/contest/996/D
解題思路


AC代碼:
#define ms(a,b) memset(a,b,sizeof a)
int e[21][21], b[1 << 21][21], n;
int main() {
//freopen("in.txt", "r", stdin);
ios::sync_with_stdio(false), cin.tie(0);
cin >> n;
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
cin >> e[i][j];
ms(b, 0x3f); b[1][0] = 0;
for (int i = 0; i < 1 << n; ++i)
for (int j = 0; j < n; ++j) if (i >> j & 1)
for (int k = 0; k < n; ++k) if (~(i >> k) & 1)//if ((i ^ 1 << j) >> k & 1)
b[i + (1 << k)][k] = min(b[i + (1 << k)][k], b[i][j] + e[j][k]);
cout << b[(1 << n) - 1][n - 1] << endl;
}
⭐例題:[NOI2014]起床困難綜合征
題意:

貪心從高位到低位枚舉,檢驗當前位在初始值為\(0\) 情況下的答案是否可以為\(1\) ,如果不能則檢驗當前位初始值能否為 \(1\),並檢驗當前位在初始值為 \(1\) 情況下的答案是否可以為 \(1\)。
int n, m, x;
string str;
pair<string, int> a[100005];
int work(int bit, int now) { // 用參加的第 bit 位進行n次運算
for (int i = 1; i <= n; ++i) {
int x = a[i].second >> bit & 1;
if (a[i].first == "AND")
now &= x;
else if (a[i].first == "OR")
now |= x;
else
now ^= x;
}
return now;
}
int main() {
ios_base::sync_with_stdio(false), cin.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; ++i) {
cin >> str >> x;
a[i] = make_pair(str, x);
}
int val = 0, ans = 0;
for (int bit = 29; bit >= 0; bit--) {
int res0 = work(bit, 0), res1 = work(bit, 1);
if (val += (1 << bit) <= m && res0 < res1)
val += (1 << bit), ans += (res1 << bit);
else
ans += (res0 << bit);
}
cout << ans << "\n";
return 0;
}
0x02 遞推與遞歸
遞歸實現指數型枚舉
int _, n, m, k, x, y;
vector<int> vec;
void calc(int x) {
if (x == n + 1) {
for (int i = 0; i < vec.size(); ++i) cout << vec[i] << " ";
cout << "\n"; // 注意一下,以后輸出回車用 "\n" 而不是 endl
return;
}
calc(x + 1), vec.push_back(x);
calc(x + 1), vec.pop_back();
}
int main() {
ios_base::sync_with_stdio(false), cin.tie(0);
cin >> n;
calc(1);
}
遞歸實現組合型枚舉
int n, m;
vector<int> vec;
void calc(int x) {
// 剪枝,如果已經選取了超過m個數,
// 或者即使選上剩下所有數也不夠m個就要提前結束搜索了 ↓
if (vec.size() > m || vec.size() + (n - x + 1) < m) return;
if (x == n + 1) {
for (int i = 0; i < vec.size(); ++i) cout << vec[i] << " ";
cout << "\n"; // 注意一下,以后輸出回車用 "\n" 而不是 endl
return;
}
calc(x + 1), vec.push_back(x);
calc(x + 1), vec.pop_back();
}
int main() {
ios_base::sync_with_stdio(false), cin.tie(0);
cin >> n >> m;
calc(1);
}
遞歸實現排列型枚舉
int n, m;
int order[20];
bool chosen[20];
void cal(int k) {
if (k == n + 1) {
for(int i = 1;i<=n;++i)
cout << order[i] << " ";
cout << endl; return;
}
for (int i = 1;i <= n; ++i) {
if (chosen[i])continue;
chosen[i] = true;
order[k] = i;
cal(k + 1);
chosen[i] = false;
}
}
int main() {
ios::sync_with_stdio(false), cin.tie(0);
cin >> n;cal(1);
}
費解的開關
const int N = 6;//因為后續操作讀取的是字符串 char g[N][N];char backup[N][N];//備份 --- 用於記錄每次枚舉第1行的情況int n;int dx[5] = {-1,0,1,0,0}, dy[5] = {0,0,0,-1,1};//用於表示當前位置及該位置的上下左右位置的偏移量 //改變當前燈及其上下左右燈的狀況void turn(int x, int y){ for(int i = 0; i < 5; i ++){ int a = x + dx[i], b = y + dy[i];//用於表示當前位置或該位置的上下左右位置 if(a >= 0 && a < 5 || b >= 0 && b < 5){ g[a][b] ^= 1;//用於'0' 和'1'的相互轉換 -----根據二者的Ascll碼值特點 } }} int main(){ cin >> n; while(n --){ for(int i = 0; i < 5; i ++) cin >> g[i];//讀取數據 int res = 10;//用於記錄操作的結果 for(int op = 0; op < 32; op ++){//枚舉第1行燈的狀態 ---- 也可以采用遞歸實現指數型枚舉 int step = 0;//用於記錄當前情況的操作步數 memcpy(backup, g, sizeof g);//備份原數組數據 ---- 因為每次枚舉都是一種全新的情況 //枚舉第一行,若燈滅,則點亮 for(int j = 0; j < 5; j ++){ if(!(op >> j & 1)){//也可以是 if(op >> j & 1) ,因為二者情況數量相同 step ++; turn(0, j);//翻轉當前燈的狀況 } } //從第一行向下遞推至倒數第二行 for(int i = 0; i < 4; i ++){ for(int j = 0; j < 5; j ++){ if(g[i][j] == '0'){//當前行當前位置燈滅 step ++; turn(i + 1, j);//改變當前行的下一行該列燈的狀況,使當前行燈亮 } } } //檢驗最后一行燈是否全亮,若存在暗燈,則此方案不成立 bool dark = false; for(int j = 0; j < 5; j ++){ if(g[4][j] == '0'){ dark = true; break; } } if(!dark) res = min(step, res); memcpy(g, backup, sizeof backup);//還原數據,用於下次方案的操作 } if(res > 6) res = -1; cout << res << endl; } return 0;}
// 另一種解int _, a[6], ans, aa[6];string s;void dj(int x, int y) { aa[x] ^= (1 << y); if (x != 1) aa[x - 1] ^= (1 << y); if (x != 5) aa[x + 1] ^= (1 << y); if (y != 0) aa[x] ^= (1 << (y - 1)); if (y != 4) aa[x] ^= (1 << (y + 1));}void pd(int p) { int k = 0; memcpy(aa, a, sizeof(a)); for (int i = 0; i < 5; ++i) if (!((p >> i) & 1)) { dj(1, i); if (++k >= ans) return; } for (int x = 1; x < 5; ++x) for (int y = 0; y < 5; ++y) if (!((aa[x] >> y) & 1)) { dj(x + 1, y); if (++k >= ans) return; } if (aa[5] == 31) ans = k;}int main() { ios_base::sync_with_stdio(false), cin.tie(0); for (cin >> _; _--;) { memset(a, 0, sizeof(a)); for (int i = 1; i <= 5; ++i) { cin >> s; // 字符串讀入更便利處理 for (int j = 1; j <= 5; ++j) a[i] = a[i] * 2 + (s[j - 1] - '0'); } ans = 7; for (int p = 0; p < (1 << 5); p++) pd(p); cout << (ans == 7 ? -1 : ans) << "\n"; } return 0;}
Strange Towers of Hanoi
#define Fi(i, a, b) for (int i = a; i <= b; ++i)int d[13], f[13];int main() { ios_base::sync_with_stdio(false), cin.tie(0); Fi(i, 1, 12) d[i] = d[i - 1] * 2 + 1; memset(f, 0x3f, sizeof f), f[1] = 1; Fi(i, 2, 12) Fi(j, 1, i) f[i] = min(f[i], 2 * f[j] + d[i - j]); Fi(i, 1, 12) cout << f[i] << "\n"; return 0;}
⭐Sumdiv (AcWing 97. 約數之和)(數論)(分治)

const int p = 9901;int pow(int x, int y) { int ret = 1; for (; y; y >>= 1) { if (y & 1) ret = 1ll * ret * x % p; x = (ll)x * x % p; } return ret;}int main() { ios::sync_with_stdio(false), cin.tie(0); int a, b, ans = 1; cin >> a >> b; if (!a) return !puts("0"); for (int i = 2, num; i * i <= a; i++) { num = 0; while (a % i == 0) a /= i, num++; if (num) ans = ans * (pow(i, num * b + 1) - 1 + p) % p * pow(i - 1, p - 2) % p; } if (a > 1) ans = ans * (pow(a, b + 1) - 1 + p) % p * pow(a - 1, p - 2) % p; cout << ans << "\n"; return 0;}
⭐Fractal Streets
題解來源:Click Here
題意:
給你一個原始的分形圖,t組數據,對於每組數據,輸入3個數n,h,o (n為在第n級,h,o為兩個房子的編號),求在第n級情況下,編號為h和o的兩個點之間的距離*10為多少。
其中,第n級分形圖形成規則如下:
- 首先先在右下角和右上角復制一遍n-1情況下的分形圖
- 然后將n-1情況下的分形圖順時針旋轉90度,放到左上角
- 最后將n-1情況下的分形圖逆時針旋轉90度 ,放到左下角
編號是從左上角那個點開始計1,沿着道路計數。
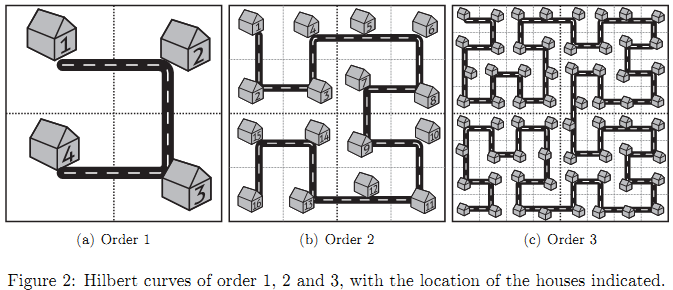
這是著名的通過一定規律無限包含自身的分形圖。為了計算方便,我們將題目中房屋編號從0開始編號,那么S與D也都減掉1.
大體思路:設calc(n,m)求編號為m的房屋編號在n級城市中的坐標位置,那么距離是:calc(n,s-1) 與 calc(n,d-1)的距離。
從n(n > 1)級城市由四座n-1級城市組成,其中:
1.左上的n-1級城市由城市結構順時針旋轉90度,從編號的順序看,該結構還做水平翻轉,坐標轉換至n級時如下圖。
2與3.右上和右下和原始城市結構一樣,坐標轉換至n級時如下圖。

市由城市結構逆時針旋轉90度,從編號的順序看,該結構也做了水平翻轉。
旋轉坐標的變化可通過公式:

(設len = 2(n-1))當旋轉角度是逆時針90度時,也就是順時針270度時,(x,y)->(y, -x),然后再進行水平翻轉,(y,-x)->(-y,-x)。然后再將圖形平移到n級圖形的左下角,在格子上的坐標變化是,水平方向增加len - 1個位置,垂直方向增加2len - 1個位置。因此坐標(x,y)按照規則轉移到了(2len-1-y,len-1-x).
注意:n-1級格子里擁有的房子數量是cnt = 22n /4,即22n-2.
當前編號m在N級格子的哪個方位是:m / cnt.
當前編號m在n-1級格子里的編號是: m %cnt;
詳細代碼如下:
using ll = long long;
pair<ll, ll> calc(ll n, ll m) {
if (n == 0) return make_pair(0, 0); //邊界
ll len = 1ll << (n - 1), cnt = 1ll << (2 * n - 2);
pair<ll, ll> zb = calc(n - 1, m % cnt);
ll x = zb.first, y = zb.second;
ll z = m / cnt;
switch (z) {
case 0: return make_pair(y, x); break;
case 1: return make_pair(x, y + len); break;
case 2: return make_pair(x + len, y + len); break;
case 3: return make_pair(2 * len - y - 1, len - x - 1); break;
}
}
int main() {
int t;
cin >> t;
while (t--) {
ll n, s, d;
cin >> n >> s >> d;
pair<ll, ll> zb;
pair<ll, ll> bz;
double ans = 0;
zb = calc(n, s - 1); //記得-1 QWQ
bz = calc(n, d - 1);
ll x, y;
x = (zb.first - bz.first), y = (zb.second - bz.second); //邊長居然是10
ans = sqrt(x * x + y * y) * 10; //喜聞樂見 勾股定理
printf("%.0f\n", ans); //四舍五入
}
return 0;
}
非遞歸實現組合型枚舉
#include <iostream>
#include <vector>
using namespace std;
vector<int> chosen;
int n, m;
void dfs(int x);
int main() {
cin >> n >> m;
dfs(1);
}
void dfs(int x) {
if (chosen.size() > m || chosen.size() + (n - x + 1) < m) return;
if (x == n + 1) {
// if(chosen.size() == 0) return;
for (int i = 0; i < chosen.size(); i++) printf("%d ", chosen[i]);
puts("");
return;
}
chosen.push_back(x);
dfs(x + 1);
chosen.pop_back();
dfs(x + 1);
return;
}
0x03 前綴和與差分
A題:HNOI2003]激光炸彈
按照藍書上的教程做即可,注意這道題卡空間用int 而不是 long long。
int g[5010][5010];
int main() {
ios_base::sync_with_stdio(false), cin.tie(0);
int N, R;
cin >> N >> R;
int xx = R, yy = R;
for (int i = 1; i <= N; ++i) {
int x, y, w;
cin >> x >> y >> w, ++x, ++y;
g[x][y] = w, xx = max(xx, x), yy = max(y, yy);
}
for (int i = 1; i <= xx; ++i)
for (int j = 1; j <= yy; ++j)
g[i][j] = g[i - 1][j] + g[i][j - 1] - g[i - 1][j - 1] +
g[i][j]; //求前綴和
int ans = 0;
for (int i = R; i <= xx; ++i)
for (int j = R; j <= yy; ++j)
//用提前算好的前綴和減去其他部分再補上多剪的那部分
ans =
max(ans, g[i][j] - g[i - R][j] - g[i][j - R] + g[i - R][j - R]);
cout << ans << "\n";
return 0;
}
B題:IncDec Sequence
設 a 的差分序列為 b.
則對區間 [l, r] 的數都加 1,就相當於 b[l]++, b[r + 1]--.
操作分為 4 種.
① 2 ≤ l ≤ r ≤ n (區間修改)
② 1 == l ≤ r ≤ n(修改前綴)
③ 2 ≤ l ≤ r == n + 1 (修改后綴)
④ 1 == l ≤ r == n + 1 (全修改)
其中操作 ④ 顯然無用.
操作 ① 性價比最高.
於是可得出方案:先用操作 ① ,使得只剩下 正數 或 負數 ,剩下的用操作 ② 或 ③ 來湊.
using ll = long long;
int main() {
ios_base::sync_with_stdio(false), cin.tie(0);
int n;
cin >> n;
vector<ll> a(n + 1, 0), b(n + 2);
for (int i = 1; i <= n; ++i) cin >> a[i], b[i] = a[i] - a[i - 1];
ll p = 0, q = 0;
for (int i = 2; i <= n; ++i) { // 2~n的正負數和統計
if (b[i] > 0) p += b[i];
else if (b[i] < 0) q -= b[i];
}
cout << max(p, q) << "\n" << llabs(p - q) + 1 << "\n";
return 0;
}
C題:Tallest Cow
差分數組,對於給出第一個區間a,b,他們之間的人肯定比他們矮,最少矮1,那么就在a+1位置-1,b位置加1,計算前綴和,a+1以及之后的都被-1了,b及以后的不變。
重復的區間,不重復計算。
另一種思路:先將所有的牛的高度都設為最大值 然后在輸入一組數A B時 將A B之間的牛的高度都減一。
map<pair<int, int>, bool> vis;
int c[10010], d[10010];
int main() {
ios_base::sync_with_stdio(false), cin.tie(0);
int n, p, h, m;
cin >> n >> p >> h >> m;
while (m--) {
int a, b;
cin >> a >> b;
if (a > b) swap(a, b);
if (vis[make_pair(a, b)]) continue; // 避免重復計算
vis[{a, b}] = true, d[a + 1]--, d[b]++;
}
for (int i = 1; i <= n; ++i) {
c[i] = c[i - 1] + d[i];
cout << h + c[i] << "\n";
}
return 0;
}
0x04 二分
⭐二分A題:Best Cow Fences
二分答案,判定是否存在一個長度不小於L的子段,平均數不小於二分的值。如果把數列中的每個數都減去二分的值,就轉換為判定“是否存在一個長度不小於L的子段,子段和非負”。
先分別考慮兩種情況的解法(1、子段和最大【無長度限制】,2、子段和最大,子段長度不小於L)
<==>求一個子段,使得它的和最大,且子段的長度不小於L。
子段和可以轉換為前綴和相減的形式,即設\(sumj\)表示\(Ai 到 Aj\)的和,
則有:\(max{A[j+1]+A[j+2].......A[i] } ( i-j>=L ) \\ = max{ sum[i] - min{ sum[j] }(0<=j<=i-L) }(L<=i<=n)\)
仔細觀察上面的式子可以發現,隨着i的增長,j的取值范圍 0~i-L 每次只會增大1。換言之,每次只會有一個新的取值進入 \(min\{sum_j\}\) 的候選集合,所以我們沒必要每次循環枚舉j,只需要用一個變量記錄當前的最小值,每次與新的取值 sum[i-L] 取min 就可以了。
double a[100001], b[100001], sum[100001];int main() { ios_base::sync_with_stdio(false), cin.tie(0); int n, L; cin >> n >> L; for (int i = 1; i <= n; ++i) cin >> a[i]; double eps = 1e-5; double l = -1e6, r = 1e6; while (r - l > eps) { double mid = (l + r) / 2; for (int i = 1; i <= n; ++i) b[i] = a[i] - mid; for (int i = 1; i <= n; ++i) sum[i] = sum[i - 1] + b[i]; double ans = -1e10; double min_val = 1e10; for (int i = L; i <= n; ++i) { min_val = min(min_val, sum[i - L]); ans = max(ans, sum[i] - min_val); } if (ans >= 0) l = mid; else r = mid; } cout << int(r * 1000) << "\n"; return 0;}
0x05 排序
A題: Cinema
經典離散化例題,把電影的語言與字幕和觀眾懂的語言放進一個數組,然后離散化。
最后統計快樂人數。
const int N = 200006;int n, m, a[N], x[N], y[N], cinema[N * 3], tot = 0, k, ans[N * 3];int find(int f) { return lower_bound(cinema + 1, cinema + k + 1, f) - cinema; }int main() { cin >> n; for (int i = 1; i <= n; ++i) cin >> a[i], cinema[++tot] = a[i]; cin >> m; for (int i = 1; i <= m; ++i) cin >> x[i], cinema[++tot] = x[i]; for (int i = 1; i <= m; ++i) cin >> y[i], cinema[++tot] = y[i]; sort(cinema + 1, cinema + tot + 1); k = unique(cinema + 1, cinema + tot + 1) - (cinema + 1); memset(ans, 0, sizeof(ans)); for (int i = 1; i <= n; i++) ans[find(a[i])]++; int ans0 = 1, ans1 = 0, ans2 = 0; for (int i = 1; i <= m; i++) { int ansx = ans[find(x[i])], ansy = ans[find(y[i])]; if (ansx > ans1 || (ansx == ans1 && ansy > ans2)) { ans0 = i; ans1 = ansx; ans2 = ansy; } } cout << ans0 << endl; return 0;}
當然不用離散化也可以做。
簡單使用 unordered_map 映射個數即可
const int N = 2e5 + 10;int _, n, x, y, tmp, a[N];unordered_map<int, int> mp;int main() { ios_base::sync_with_stdio(false), cin.tie(0); for (cin >> _; _--;) cin >> tmp, mp[tmp]++; cin >> n; for (int i = 1; i <= n; ++i) cin >> a[i]; for (int i = 1; i <= n; ++i) { int t; cin >> t; if (mp[a[i]] > x) tmp = i, x = mp[a[i]], y = mp[t]; else if (mp[a[i]] == x && mp[t] > y) tmp = i, y = mp[t]; } cout << tmp << "\n"; return 0;}
B題:貨倉選址
排序一下,利用中位數的性質
int n, ans, sum;int main() { ios_base::sync_with_stdio(false), cin.tie(0); cin >> n; vector<int> v(n); for (auto &t : v) cin >> t; sort(v.begin(), v.end()); ans = v[n / 2]; for (auto &t : v) sum += abs(t - ans); cout << sum << "\n"; return 0;}
C題:⭐七夕祭
這里借下 洛凌璃dalao的blog題解
題解
這個題其實是兩個問題:
1.讓攤點上下移動,使得每行的攤點一樣多
2.左右移動攤點,使得每列的攤點一樣多
兩個問題是等價的,就討論第一個
r[i]表示每行的攤點數
然后使得r[i]的一些攤點移動到r[i - 1]和r[i + 1], 類似於"均攤紙牌"
均攤紙牌
有M個人排一排,每個人分別有C[1]~C[M]張拍,每一步中,一個人可以將自己的一張手牌給相鄰的人,求至少需要幾步
顯然, 紙牌總數T能被M整除有解,在有解的情況下, 考慮第一個人:
1.C[1] >= T/M, 第一個人要給第二個人C[1] - T/M張牌
2.C[1] < T/M, 第二個給第一個人T/M - C[1]張牌
本質就是使得第一人滿足要求要|T/M - C[1]|步
那么滿足第二人就要 |T/M - (C[2] - (T/M - C[1]))| = |2 * T/M - (C[1] + C[2])|步
滿足第三人 |T/M - (C[3] - (T/M - (C[2] - (T/M - C[1]))))| = |3 * T/M - (C[1] + C[2] + C[3])|
到這里就可以發現,有一段是前綴和, 但再仔細化簡以下可以發現
|3 * T/M - (C[1] + C[2] + C[3])|
=|(T/M - C[1]) + (T/M - C[2]) + (T/M - C[3])|
=|(C[1] - T/M) + (C[2] - T/M) + (C[3] - T/M)|
我們可以讓A[i] = C[i] - T/M, S[i]為A[i]的前綴和,
那么對於"均攤紙牌"這道題的答案就是
∑ni=1∑i=1n|S[i]|
對於本題來說,無非是變成了環形問題
直接無腦dp就可以
我們隨便選取一個人k最為斷環的最后一名(即第一個人變為為k + 1),
則從這個人開始的持有的牌數(這行的攤點數), 前綴和為
A[k + 1] S[k + 1] - S[k]A[k + 2] S[k + 2] - S[k]...A[M] S[M] - S[k]A[1] S[M] - S[k] + S[1]A[2] S[M] - S[k] + S[2]...A[k] S[M] - S[k] + S[k]
我們發現S[M] = 0, 所以答案為
|S[k + 1] - S[k]| + ... + |S[M] - S[k]| + |s[M] - S[k] + S[1]| + ... + |S[M] - S[K] + S[k]|
=|S[k + 1] - S[k]| + ... + |S[M] - S[k]| + |-S[k] + S[1]| + ... + |-S[k] + S[k]|
=∑ni=1∑i=1n |S[i] - S[k]|
答案已經很明顯了,像不像"倉貨選址"?
倉貨選址
一條軸上有N家店,每家店的坐標為D[1]~D[N],選擇一家點為倉庫向其他商店發貨,求選哪家店,運送距離最短
不就是∑ni=1∑i=1n |D[i] - D[k]| 為答案嗎?
當然是選中位數了啦,
設k左邊有P家店,右邊有Q家店
如果P<Q,那必然將k右移, ans - Q + P,答案明顯變小了
Q>P,同理,故選擇中位數
所以本題的答案就已經近在眼前了, 前綴和,求中位數
using ll = long long;
const int maxn = 1e5 + 5;
int n, m, k;
int c[maxn], r[maxn], s[maxn];
ll work(int a[], int n) {
for (int i = 1; i <= n; ++i) s[i] = s[i - 1] + a[i] - k / n;
sort(s + 1, s + 1 + n);
ll ans = 0;
for (int i = 1; i <= n; ++i) ans += abs(s[i] - s[(n >> 1) + 1]);
return ans;
}
int main() {
cin >> n >> m >> k;
for (int i = 1; i <= k; ++i) {
int a, b;
cin >> a >> b, ++c[b], ++r[a];
}
if (k % n + k % m == 0)
cout << "both " << work(c, m) + work(r, n);
else if (k % n == 0)
cout << "row " << work(r, n);
else if (k % m == 0)
cout << "column " << work(c, m);
else
cout << "impossible";
return 0;
}
0x06 倍增
⭐例題 Genius_ACM
考慮到二分會有很多低效的操作(如:二分第一步檢驗 \([N - L] / 2\) 這么長一段但右端點只會移動很少的部分),直接換倍增寫。
- 初始化 \(p = 1,R = L\)
- 求出 \([L,R + p]\) 區間的“檢驗值” ,若 檢驗值 \(\le T\) 則 \(R += p,p *=2\) ,否則 \(p /=2\)
- 重復上一步直到 \(p = 0\) ,此時 R 為所求值
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 500006;
int n, m, w;
ll k, a[N], b[N], c[N];
void gb(int l, int mid, int r) {
int i = l, j = mid + 1;
for (int k = l; k <= r; k++)
if (j > r || (i <= mid && b[i] <= b[j])) c[k] = b[i++];
else
c[k] = b[j++];
}
ll f(int l, int r) {
if (r > n) r = n;
int t = min(m, (r - l + 1) >> 1);
for (int i = w + 1; i <= r; i++) b[i] = a[i];
sort(b + w + 1, b + r + 1);
gb(l, w, r);
ll ans = 0;
for (int i = 0; i < t; i++)
ans += (c[r - i] - c[l + i]) * (c[r - i] - c[l + i]);
return ans;
}
void Genius_ACM() {
cin >> n >> m;
cin >> k;
for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);
int ans = 0, l = 1, r = 1;
w = 1;
b[1] = a[1];
while (l <= n) {
int p = 1;
while (p) {
ll num = f(l, r + p);
if (num <= k) {
w = r = min(r + p, n);
for (int i = l; i <= r; i++) b[i] = c[i];
if (r == n) break;
p <<= 1;
} else
p >>= 1;
}
ans++;
l = r + 1;
}
cout << ans << endl;
}
int main() {
int t;
cin >> t;
while (t--) Genius_ACM();
return 0;
}
0x30 數學知識
0x31 質數
【例題】質數距離
【例題】階乘分解
0x32 約數
AcWing 198. 反素數
AcWing 199. 余數之和
AcWing 200. Hankson的趣味題
AcWing 201. 可見的點
0x33 同余
AcWing 202. 最幸運的數字
AcWing 203. 同余方程
AcWing 204. 表達整數的奇怪方式
0x34 矩陣乘法
AcWing 205. 斐波那契
AcWing 206. 石頭游戲
0x35 高斯消元與線性空間
AcWing 207. 球形空間產生器
AcWing 208. 開關問題169人打卡
AcWing 209. 裝備購買
AcWing 210. 異或運算
0x36 組合計數
AcWing 211. 計算系數
AcWing 212. 計數交換
AcWing 213. 古代豬文
0x37 容斥原理與Mobius函數
AcWing 214. Devu和鮮花
AcWing 215. 破譯密碼
0x38概率與數學期望
AcWing 216. Rainbow的信號
AcWing 217. 綠豆蛙的歸宿
AcWing 218. 撲克牌
0x39 0/1分數規划
0x40 博弈論之SG函數
AcWing 219. 剪紙游戲
0x50 動態規划
0x51 線性DP
【例題】Mr. Young's Picture Permutations
容易發現最高的人只能站在最左上角,然后后面的人從高到低必須要站在已經有的人的附近,不然就不合法。
以此為依據,以人數為階段,每一排的人數為狀態轉移即可。可以使用隊列保證狀態轉移順序正確。
詳細操作

事實上這個題考的是一個叫做楊氏矩陣的數據結構,有興趣的話可自行了解。
using ll = long long;
int n[6], k;
void solve() {
for (int i = 1; i <= k; ++i) cin >> n[i];
while (k < 5) n[++k] = 0;
ll f[n[1] + 1][n[2] + 1][n[3] + 1][n[4] + 1][n[5] + 1];
memset(f, 0, sizeof(f));
f[0][0][0][0][0] = 1;
for (int i = 0; i <= n[1]; i++)
for (int j = 0; j <= n[2]; j++)
for (int k = 0; k <= n[3]; k++)
for (int l = 0; l <= n[4]; l++)
for (int m = 0; m <= n[5]; m++) {
if (i < n[1]) f[i + 1][j][k][l][m] += f[i][j][k][l][m];
if (j < n[2] && i > j)
f[i][j + 1][k][l][m] += f[i][j][k][l][m];
if (k < n[3] && j > k)
f[i][j][k + 1][l][m] += f[i][j][k][l][m];
if (l < n[4] && k > l)
f[i][j][k][l + 1][m] += f[i][j][k][l][m];
if (m < n[5] && l > m)
f[i][j][k][l][m + 1] += f[i][j][k][l][m];
}
cout << f[n[1]][n[2]][n[3]][n[4]][n[5]] << endl;
}
【例題】LCIS
LCS + LIS 綜合考慮的問題,即求兩個序列的最長公共上升子序列。
仿照求最長公共子序列和最長上升子序列的做法,定義 \(f[i][j]\) 為序列 \(A\) 中前 i 個元素和序列 \(B\) 以 j 為結尾的最長公共上升子序列,狀態轉移方程:
一般可以寫三層循環來完成遞推,
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j) {
if (a[i] == b[j]) {
for (int k = 0; k < j; ++k)
if (b[k] < a[i]) f[i][j] = max(f[i][j], f[i - 1][k] + 1);
} else
f[i][j] = f[i - 1][j];
}
但 \(max_{0\le k< j,B_k< B_j}\{f(i - 1,k) + 1\) 這一部分只與當前的 \(a[i]\) 和之前的 \(b[j]\) 有關可以對於每個 i 單獨維護它的值,最終時間復雜度為 \(O(n^2)\).
#include <bits/stdc++.h>
using namespace std;
const int N = 3001;
int ans, n, a[N], b[N], f[N];
int main() {
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++) cin >> b[i];
for (int i = 1; i <= n; i++)
for (int j = 1, val = 0; j <= n; j++)
if (a[i] == b[j]) f[j] = val + 1;
else if (b[j] < a[i])
val = max(val, f[j]);
for (int i = 1; i <= n; i++) ans = max(ans, f[i]);
return printf("%d", ans), 0;
}
⭐Making the Grade
這道題強烈建議看書:P268
題目大意是給出一個長度為 n 的序列,要求使序列變為單調上升或單調不減序列(非嚴格),問花費的最少代價?
把 A 序列出現的數進行離散化,把DP狀態中第二維 \(j\) 降到 \(O(N)\)
轉移方程是: \(dp[i][j]\)表示前 \(i\) 個元素的最后一個元素為全部元素第 \(j\) 大時的最小代價
#include <bits/stdc++.h>
using namespace std;
const int N = 2010;
int a[N], c[N], nums[N];
int f[N][N];
int n;
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
nums[i] = a[i];
}
sort(nums + 1, nums + n + 1);
int m = unique(nums + 1, nums + n + 1) - nums - 1;
for (int i = 1; i <= n; i++)
c[i] = lower_bound(nums + 1, nums + m + 1, a[i]) - nums;
memset(f, 0x3f, sizeof(f));
f[0][0] = 0;
for (int i = 1; i <= n; i++) {
int temp = f[i - 1][0];
for (int j = 1; j <= m; j++) {
temp = min(temp, f[i - 1][j]);
f[i][j] = temp + abs(a[i] - nums[j]);
}
}
int ans = 1 << 30;
for (int i = 1; i <= m; i++) ans = min(ans, f[n][i]);
cout << ans << endl;
}
⭐Mobile Service
有3個員工起始在1,2,3個位置
他們要去p1,p2...pN按順序完成任務 N<=2000,位置有200個
移動的代價為\(c[x][p1]\) 從x到p1
要求一個位置不能同時被兩個員工占領求完成所有P后代價最少為多少
顯然階段為Pi
需要記錄3個狀態,3個員工的位置,直接記錄的話內存不夠
我們可以發現在階段i,必定有一個員工在pi,所以我們只需要記錄另外兩個員工的位置就好
void solve() { //f[i][x][y] 表示完成了前i個任務,3個員工的位置分別為 x,y,p[i]的最小花費 f[0][1][2] = 0; p[0] = 3; // 分別dp,從p[i-1]到p[i],x到p[i],y到p[i] f[i][x][y] = min(f[i][x][y], f[i - 1][x][y] + c(p[i - 1], p[i])) x != p[i], y != p[i]; f[i][p[i - 1]][y] = min(f[i][p[i - 1]][y], f[i - 1][x][y] + c(x, p[i])) p[i - 1] != p[i], y != p[i]; f[i][x][p[i - 1]] = min(f[i][x][p[i - 1]], f[i - 1][x][y] + c(y, p[i])) p[i - 1] != p[i], x != p[i];}
AC 代碼
using ll = long long;const int L = 210, N = 1010, inf = 0x3f3f3f3f;int l, n, c[L][L], p[N], f[N][L][L];void solve() { memset(f, 0x3f, sizeof(f)); cin >> l >> n; for (int i = 1; i <= l; ++i) for (int j = 1; j <= l; ++j) cin >> c[i][j]; p[0] = 3; f[0][1][2] = 0; for (int i = 1; i <= n; ++i) { cin >> p[i]; for (int j = 1; j <= l; ++j) for (int k = 1; k <= l; ++k) { if (f[i - 1][j][k] != inf) { if (j != p[i] && k != p[i]) f[i][j][k] = min(f[i][j][k], f[i - 1][j][k] + c[p[i - 1]][p[i]]); if (j != p[i] && p[i - 1] != p[i]) f[i][j][p[i - 1]] = min(f[i][j][p[i - 1]], f[i - 1][j][k] + c[k][p[i]]); if (k != p[i] && p[i - 1] != p[i]) f[i][p[i - 1]][k] = min(f[i][p[i - 1]][k], f[i - 1][j][k] + c[j][p[i]]); } } } int ans = inf; for (int i = 1; i <= l; ++i) for (int j = 1; j <= l; ++j) ans = min(ans, f[n][i][j]); cout << ans;}
⭐傳紙條
----------------------------
有這么一些狀態
步數i,兩個狀態(x1,y1)(x2,y2)
我們考慮尋找能夠覆蓋整個狀態空間的最小的 "維度集合"
由於每次兩個坐標只能走一次
所以我們可以觀察到步數和坐標之間的關系有:
i+2 = x1+y1 = x2+y2
所以我們可以維護3個狀態f[橫縱坐標和][x1][x2]
那么可以通過橫縱坐標和 以及 x1,x2
求出(x1,y1),(x2,y2)
轉移方程:
每個點可以有前面的兩個點轉移過來,2*2=4
所以每個狀態可以由四種狀態轉移過來,取最大
f[x1][y1][x2][y2] <====
max(f[x1-1][y1][x2-1][y2],
f[x1-1][y1][x2][y2-1],
f[x1][y1-1][x2-1][y2],
f[x1][y1-1][x2][y2-1]) + a[x1][y1] + a[x2][y2];
對應為:
f[i][x1][x2] <=====
max(f[i-1][x1-1][x2],f[i-1][x1-1][x2-1],
f[i-1][x1][x2-1],f[i-1][x1][x2-1]) + a[x1][y1] + a[x2][y2];
using ll = long long;
const int N = 60;
int f[N << 1][N][N], a[N][N];
void solve() {
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) cin >> a[i][j];
for (int i = 0; i < n + m - 2; i++)
for (int j = 1; j <= n && j <= i + 1; j++)
for (int k = 1; k <= n && k <= i + 1; k++) {
if (j == k) {
f[i + 1][j][k] =
max(f[i + 1][j][k], f[i][j][k] + a[j][i + 3 - j]);
f[i + 1][j + 1][k + 1] =
max(f[i + 1][j + 1][k + 1],
f[i][j][k] + a[j + 1][i + 2 - j]);
} else {
f[i + 1][j][k] =
max(f[i + 1][j][k],
f[i][j][k] + a[j][i + 3 - j] + a[k][i + 3 - k]);
f[i + 1][j + 1][k + 1] = max(
f[i + 1][j + 1][k + 1],
f[i][j][k] + a[j + 1][i + 2 - j] + a[k + 1][i + 2 - k]);
}
if (j + 1 == k)
f[i + 1][j + 1][k] = max(f[i + 1][j + 1][k],
f[i][j][k] + a[j + 1][i + 2 - j]);
else
f[i + 1][j + 1][k] =
max(f[i + 1][j + 1][k],
f[i][j][k] + a[j + 1][i + 2 - j] + a[k][i + 3 - k]);
if (k + 1 == j)
f[i + 1][j][k + 1] =
max(f[i + 1][j][k + 1], f[i][j][k] + a[j][i + 3 - j]);
else
f[i + 1][j][k + 1] =
max(f[i + 1][j][k + 1],
f[i][j][k] + a[j][i + 3 - j] + a[k + 1][i + 2 - k]);
}
cout << f[n + m - 2][n][n] << endl;
}
⭐Cookies
CH5105 Cookies
聖誕老人共有M個餅干,准備全部分給N個孩子。每個孩子有一個貪婪度,
第 i 個孩子的貪婪度為 g[i]。如果有 a[i] 個孩子拿到的餅干數比第 i 個孩子多,
那么第 i 個孩子會產生 g[i]*a[i]的怨氣。給定N、M和序列g,
聖誕老人請你幫他安排一種分配方式,使得每個孩子至少分到一塊餅干,
並且所有孩子的怨氣總和最小。1≤N≤30, N≤M≤5000, 1<=gi<=10^7。
--------------------------------------------------------------------------
安排啊方案啊...N,M都比較小,可以DP,不會啊...
"已經獲得餅干的孩子","已經發放的餅干",可以作為階段
然后一個孩子的g值會影響他獲得的餅干數
貪心策略的g值高的孩子獲得的餅干數多
可以交換兩個值進行比較證明.
設g[i]>g[i-1]>g[i-2]...
獲得餅干 c[i]>c[i-1]>c[i-2]...
貢獻值 X = 0*g[i]+1*g[i-1]+2*g[i-2]...
g[i]>g[i-1]>g[i-2]...
獲得餅干 c[i-1]>c[i]>c[i-2]...
貢獻值 Y = 0*g[i-1]+1*g[i]+2*g[i-2]...
g[i] > g[i-1] 顯然Y>X...故用X
a[i]為第i個孩子的餅干數
對於第i+1個孩子餅干數有兩種選擇,要么等於第i個孩子,要么少於第i個孩子a[i+1]=i
可是我們必須知道a[i],但是很難維護....
畫出餅干遞減的柱形圖
發現若第i個孩子餅干數大於1的話,
則等價於把前i個孩子的餅干數都減少1
因為餅干數的相對大小順序不變,所以總貢獻也不變
f[i][j] <=== f[i][j-i]
然后,若第i個孩子的餅干數為1的話,
則枚舉i前面有k個孩子的餅干數等於1
f[i][j] <=== min( f[k][j-(i-k)] + k*(g[k+1]~g[i]) )
0x52 背包
0x53 區間DP
0x54樹形DP
0x55 環形與后效性處理
AcWing 288. 休息時間
題目描述
把一天划分為 \(N\) 個時間段,每天總共需要休息 \(M\) 個時間段,第 ii 時間段休息可以恢復 \(u_i\) 體力,每次休息過程中第一個時間段無法恢復體力。需要最大化每天能獲得的體力。
解法
注:本題作為藍書中的例題,代表了一類必須掌握的題型,推薦在參照題解前先嘗試自己完成代碼。
一道顯然的 \(DP\) 題目。經過分析可得知每個時刻的最優解受到三個因素影響:當前時刻、當前總休息時間及當前時刻是否休息。因此我們用 \(f_{i,j,k}=0/1\) 表示狀態,即第 \(i\) 時刻為止共休息 \(j\) 個時間段的最優解,\(k\) 表示當前時間段是否正在休息。
本題安排的休息時間可以跨越一天的最后一個時間段,即當天休息后第二天再醒來,因此本題的模型是一個環形模型。
處理環形模型一般使用分類討論與斷環為鏈兩種解法,本篇題解重點介紹第一種。
不難發現,我們可以把安排的方案分為兩種類型。
- 最后一個時間段不休息,此時本題轉化為線性模型;
- 第一個時間段休息。
首先考慮第一種情況。線性模型求解不會受到后效性的影響,我們可以輕松寫出對應的方程:
最終答案 \(ans=max\{f_{N,M,0},f_{N,M,1}\}\)。
接着考慮第二種情況。我們發現這種情況與上文中的第一種情況幾乎沒有差異,唯一的不同點是在這種情況下第一時間段能夠恢復一些體力,而上一種不可以。因此只需要強制令 \(f_{i,1,1}=u_1\),重復上述過程即可。最終答案 \(ans=max\{ans,f_{N,M,1}\}\).
本題是否已經被完全解決了?也許並沒有。本題的空間限制僅有64 MB,這樣的代碼一定會 MLE。因此需要考慮進一步的優化。
我們發現,在求\(f_{i,j,k}\) 的過程中只用到了 \(f_{i−1,j,k}\) 的值,與\(i−1\) 之前時刻的解無關。因此可以使用滾動數組優化,用 i&1 代替 \(i\)。這樣一來,程序使用的空間大大減少,能夠通過本題。
至此,本題得到完美解決。
注:切記\(DP\) 的邊界條件與 \(f\) 數組的初始化。
有關環形模型的第二種處理方式,即斷環為鏈,可以參考藍書中的下一道例題: AcWing289 環路運輸。
int n, b, ans = 0, T;
int f[2][3831][2], a[3831];
int Max(int a, int b) {return a > b ? a : b;}
int Min(int a, int b) {return a < b ? a : b;}
void solve() {
cin >> n >> b;
for (int i = 1; i <= n; ++i)cin >> a[i];
memset(f, 128, sizeof(f));//初始化為負無窮
f[1][0][0] = f[1][1][1] = 0;//邊界條件
// 第n小時不在睡覺,情況1
for (int i = 2; i <= n; ++i)
for (int j = 0; j <= Min(b, i); ++j) {
f[i & 1][j][0] = Max(f[(i - 1) & 1][j][0], f[(i - 1) & 1][j][1]);
if (j)f[i & 1][j][1] = Max(f[(i - 1) & 1][j - 1][0],
f[(i - 1) & 1][j - 1][1] + a[i]);
}
ans = Max(ans, Max(f[n & 1][b][0], f[n & 1][b][1]));
memset(f, 128, sizeof(f));
f[1][1][1] = a[1];
for (int i = 2; i <= n; i++) { //情況 2
for (int j = 0; j <= Min(b, i); j++) {
f[i & 1][j][0] = Max(f[(i - 1) & 1][j][0], f[(i - 1) & 1][j][1]);
if (j)f[i & 1][j][1] = Max(f[(i - 1) & 1][j - 1][0],
f[(i - 1) & 1][j - 1][1] + a[i]);
}
}
ans = Max(ans, f[n & 1][b][1]);
cout << ans << "\n";
}
AcWing 289. 環路運輸
題目描述
環上有 \(N\) 個點,每個點有點權 \(A_i\),相鄰倉庫距離為 1,任意兩點 i,j 之間的距離定義為沿環的兩側分別從 i 前往 j 的距離中的較小值。定義任意兩點 i,j 之間的代價為 \(A_i+A_j+dis_{i,j}\),求環上最大代價。
解法
注:本題作為藍書中的例題,代表了一類必須掌握的題型,推薦在參照題解前先嘗試自己完成代碼。
不難看出使用 \(DP\) 求解的基本思路。
本題為環狀模型,處理起來有一定難度。處理環狀模型有兩種常用方法:分類討論與斷環為鏈。如想要了解分類討論的思想,可以參照藍書中的上一道例題 AcWing288 休息時間。下面主要介紹斷環為鏈的思想。
斷環為鏈的思想可以簡述為:對於一個長度為 N 的環,我們不妨將其斷開並延長一倍,使之變成一條長度為 2N 的鏈,並將其划分為若干部分分別考慮。
首先把題面中計算代價的算式拆開,可以得到:
在斷環為鏈之后,該算式等價於:在長度為 2N 的鏈上,
此時,本題已經被轉化為了標准的線性 DP。
下面我們考慮如何求解該線性模型。如果按照上文推出的算式進行 DP,我們需要一維枚舉 i,一維枚舉 j,總時間復雜度為 \(O(N^2)\)。本題中 \(N≤10^6\),這樣的復雜度無法令人滿意。考慮優化。
繼續觀察算式,我們發現該算式可以轉化為如下形態:
其中,當 \(i\) 固定時,\((Ai+i)\) 也確定了下來,我們只需要考慮 \((Aj−j)\) 的最大值即可。
考慮對這一部分使用單調隊列維護(參見藍書 0x59 節)。通過這種方式,我們可以在 \(O(1)\) 的時間內得到這一部分的最大值。
均攤時間復雜度為 \(O(N)\),可以通過本題。
至此,本題得到完美解決。
using ll = long long;
const int N = 2e6 + 10;
int a[N], q[N], h = 1, t = 0, n;
ll ans;
void solve() {
cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> a[i];
a[i + n] = a[i];
}
int len = n / 2;
q[++t] = 1;
for (int i = 2; i <= n + len; ++i) {
while (q[h] < i - len and h <= t)h++;
ans = max(ans, 1ll * (a[i] + i + a[q[h]] - q[h]));
while (a[q[t]] - q[t] < a[i] - i and t >= h)t--;
q[++t] = i;
}
cout << ans;
}
0x59單調隊列優化DP
AcWing 298. 圍欄
狀態轉移依然不錯
f[i][j]表示第i個木匠刷到j總共的報酬
將題中的木匠按 \(s\) 進行排序,只會更新 \(j>=s\) 的,保證沒有后效性
\(f[i][j]=max(f[i-1][j],f[i][j-1]);\) 表示可以i木匠不刷或者當前的木板不刷
\(f[i][j]=max( f[i][j],f[i-1][k]+p[i]*(j-k) ) j>=si,j-k>=li;\)
當i固定時
尋找k的過程可以用單調隊列優化
當j++時k的選擇范圍增加了1
將方程中與k有關的部分放到單調隊列中
維護一個 \(f[i-1][k]-p[i]*k\) 單減,k單增的隊列,即可完成轉移
typedef pair<int, int> pii;
const int N = 16010, M = 110;
struct node {
int l, p, s;
} a[M];
int n, m, dp[M][N];
bool cmp(node a, node b) { return a.s < b.s; }
void solve() {
int n, m;
cin >> n >> m;
for (int i = 1; i <= m; ++i) cin >> a[i].l >> a[i].p >> a[i].s;
sort(a + 1, a + 1 + m, cmp);
for (int i = 1; i <= m; ++i) {
deque<pii> q1;
for (int j = 0; j <= n; ++j) {
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
if (j >= a[i].s) {
while (q1.size() and q1.front().second < j - a[i].l) q1.pop_front();
if (q1.size()) dp[i][j] = max(dp[i][j],
q1.front().first + a[i].p * j);
} else {
while (q1.size()
and q1.back().first <= dp[i - 1][j] - a[i].p * j) q1.pop_back();
q1.push_back({dp[i - 1][j] - a[i].p * j, j});
}
}
}
cout << dp[m][n] << '\n';
}
