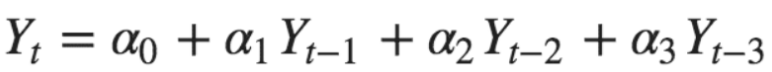經典的時間序列預測方法都是假設如果一個時間序列有顯著的自相關性,那么歷史值對預測當前值會很有幫助,但是究竟取多少階的歷史值,就需要通過分析相關函數圖和偏相關函數圖來得到。本文介紹如何什么是相關函數圖和偏相關函數圖,另外還會介紹一下滯后圖。
什么是自相關和偏自相關函數?
- 先來解釋下滯后階數n,如果當前值和前2期的值有關,則n=2,那么可以用時間序列和它的2階滯后序列來訓練一個自回歸模型,預測未來的值。
- 自相關函數(ACF)表達了時間序列和n階滯后序列之間的相關性(考慮了中間時刻的值的影響,比如t-3對t的影響中,就同時考慮了t-2,t-1對t的影響)。
- 偏自相關函數(PACF)表達了時間序列和n階滯后序列之間的純相關性(不考慮中間時刻的值的影響,比如t-3對t的影響中,不會考慮t-2,t-1對t的影響)。如果用自回歸方程來預測t時刻的值,則各滯后階數的系數就是各滯后階數下的偏自相關值,比如下面方程的α1,α2,α3,分別是1階滯后,2階滯后,3階滯后下的偏自相關值。
ACF 和 PACF 可視化
from statsmodels.tsa.stattools import acf, pacf
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv')
# Calculate ACF and PACF upto 50 lags# acf_50 = acf(df.value, nlags=50)# pacf_50 = pacf(df.value, nlags=50)
# Draw Plot
fig, axes = plt.subplots(1,2,figsize=(16,3), dpi= 100)
plot_acf(df.value.tolist(), lags=50, ax=axes[0])
plot_pacf(df.value.tolist(), lags=50, ax=axes[1])
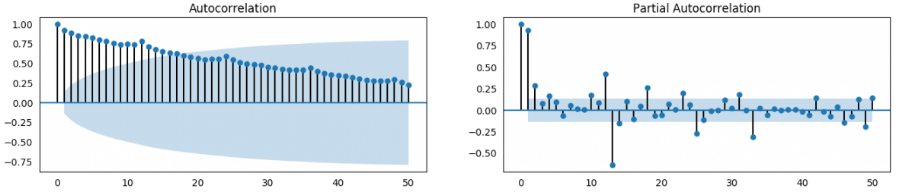
- 如果ACF表現為長拖尾(如上左圖),說明帶有趨勢,需要做差分。
- 如果ACF的1階滯后就截尾,則可能是過度差分了(差分會降低相關性)。
- 如果ACF拖尾一點點,然后截尾的情況下,選擇的差分階數是比較合適的。此時可以用前n個歷史時刻的值做自回歸來預測當前值,關於n的取值則可以參考PACF的截尾處,假設上右圖是差分后的pacf圖,在第2個滯后階數后(從第0開始,0階滯后下就是原序列和原序列相比,相關性為1)就驟然降到了相關性置信區間內,則表示95%的概率不具有相關性,所以該序列可以做2階滯后自回歸。
什么是相關性置信區間?
對於白噪聲序列,按理說不會有任何自相關性,我們期望的自相關性為0,但是由於隨機擾動的存在,自相關性不會為0,而通常假設隨機擾動符合標准正態分布(均值為0,標准差為1),那么這個隨機擾動的95%置信區間(一般都取95%,當然也可以調整這個概率)可以通過如下算式計算
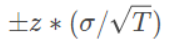
標准正態分布的z分數表示距離均值有幾個標准差,σ除以根號T表示有偏樣本標准差,
這里95%置信度下z分數=1.96,標准差σ=1,T是序列長度,則置信區間計算如下:

表示對於白噪聲序列,95%的自相關性落在這個置信區間內。
而這個置信區間就是上面acf和pacf圖中的相關性區間了,也就是說如果滯后階數與原序列的相關性落在這個區間內,就表示不相關。
滯后圖
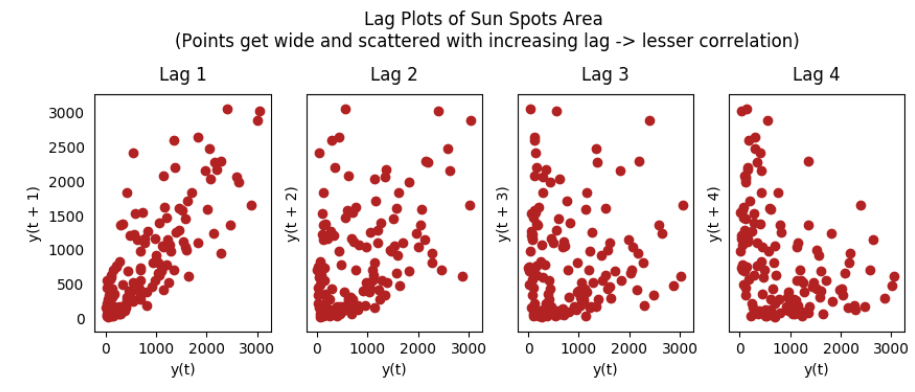
滯后圖是用時間序列和相應的滯后階數序列做出的散點圖。可以用於觀測自相關性。
from pandas.plotting import lag_plot
plt.rcParams.update({'ytick.left' : False, 'axes.titlepad':10})
# Import
ss = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/sunspotarea.csv')
a10 = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv')
# Plot
fig, axes = plt.subplots(1, 4, figsize=(10,3), sharex=True, sharey=True, dpi=100)for i, ax in enumerate(axes.flatten()[:4]):
lag_plot(ss, lag=i+1, ax=ax, c='firebrick')
ax.set_title('Lag ' + str(i+1))
fig.suptitle('Lag Plots of Sun Spots Area \n(Points get wide and scattered with increasing lag -> lesser correlation)\n', y=1.15)
fig, axes = plt.subplots(1, 4, figsize=(10,3), sharex=True, sharey=True, dpi=100)for i, ax in enumerate(axes.flatten()[:4]):
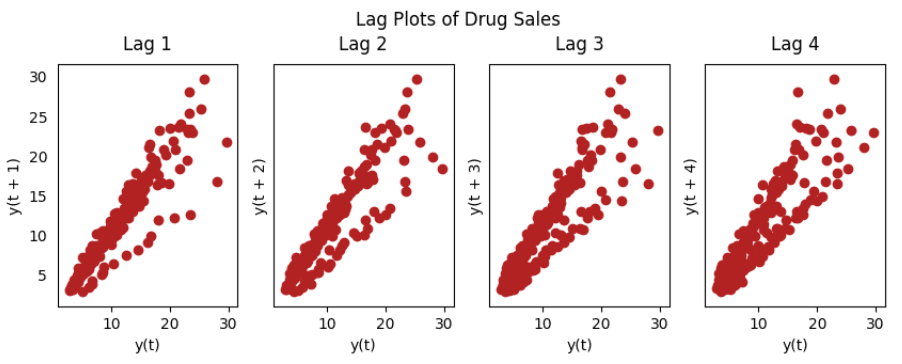
lag_plot(a10, lag=i+1, ax=ax, c='firebrick')
ax.set_title('Lag ' + str(i+1))
fig.suptitle('Lag Plots of Drug Sales', y=1.05)
plt.show()
ok,本篇就這么多內容啦~,感謝閱讀O(∩_∩)O。