NFA到DFA的轉換

一、有限自動機

1、不確定的有限自動機（NFA）

• 只要有一條路徑能夠使一個字符串從初始態到達接收態就稱這個字符串是接收的
• 匹配結果，是不確定的
• 慢，有Backtrack（回溯）
• 基於表達式
• 某時刻可能處於一組狀態之中的任何一個，因此記錄所有的可能路徑

2、確定的有限自動機（DFA）

• 匹配速度，是確定的
• 快，無Backtrack（回溯）
• 基於文本
• 在任意時刻必定處於某個確定狀態

二、NFA到DFA轉換

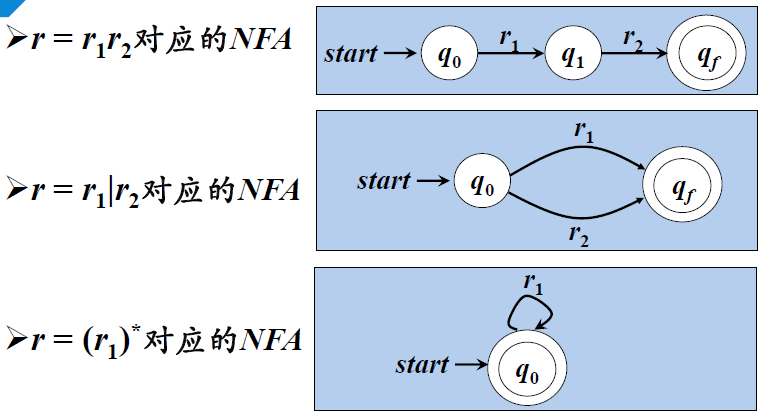
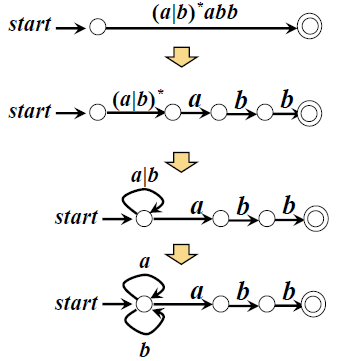
1、根據RE構造NFA

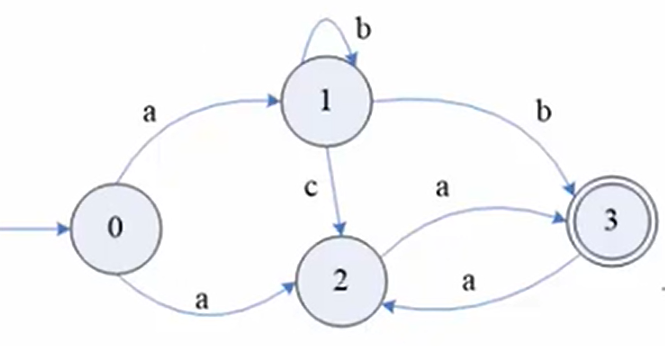
2、NFA轉為DFA

又稱NFA的確定化

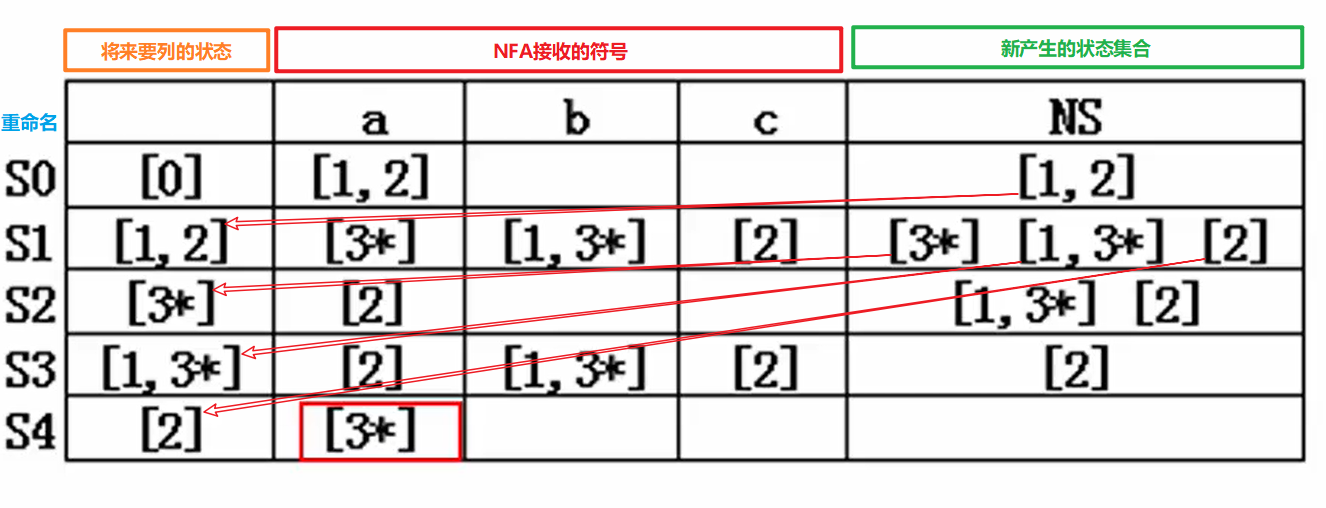
狀態轉換表

注：標有*為接收狀態 帶ε

邊記得增加一列

1. NFA的開始狀態集合為[0]，將NFA將接收的符號代入當前狀態，最長子串原則，得出新產生的狀態
2. 將新產生的狀態作為將來要列出的狀態重復1中步驟
3. 直至新產生的狀態集合中無新集合時結束
4. 將第一列中將來要列的狀態重命名

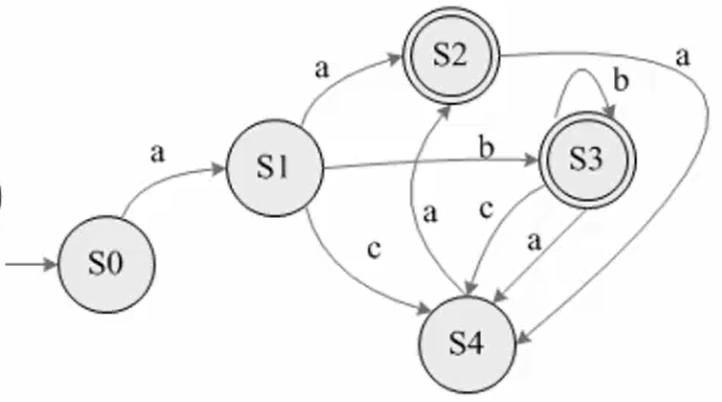
轉換為DFA

1. S₀為初始狀態，根據狀態轉換表中NFA接受的符號產生的集合到重命名中尋找匹配的狀態
2. 畫圖，根據新的圈重復1中步驟，直至結束
3. 重命名中標有*的接受態要用雙圈標出

 

計算ε-closure(T)：