1數據流分析基礎
1.1停機問題-抽象方法
針對基礎篇中的停機問題,我們可以試用抽象方法去嘗試解決問題。邪惡程序存在的關鍵在於程序中有if存在 。因此可以采取以下方式。
1.1.1忽略掉所有程序的if條件部分
void Evil(){
if(!Halt(Evil))return;
else while(1)
}
抽象成
void Evil(){
向左走return;
向右走while(1);
}
語義:“向左走/向右走”為非確定性選擇,程序隨機從“向左走” 和“向右走”后面的語句中選擇一條執行。
1.1.2忽略所有條件判斷中的條件,一律抽象為不確定選擇
void Evil(){
再來一次
向左走goto再來一次;
向右走return;
}
1.1.3抽象過程分析
針對給定輸入
- 原始程序只有一條執行路徑,抽象程序上有多條執行路徑
- 原始程序的執行路徑一定包含在抽象程序的執行路徑中
停機問題
- 原始程序停機:存在自然數n,程序的執行路徑長度 小於n
- 抽象程序停機:存在自然數n,程序中所有執行路徑 的長度都小於n
1.1.4停機問題的判定方法
繪制控制流圖(結點為程序語句,邊為語句間的轉移 ), 如果控制流圖上有環,則可能不終止,否則一定終止。
1.2符號分析
1.2.1分析內容
給定一個只包含浮點數變量和常量的程序,已知輸入的符號,求輸出的符號。
1.2.2符號分析的抽象
抽象符號
- 正 ={所有的正數}
- 零={0}
- 負= {所有的負數}
- 槑={所有的整數和NaN}
1.2.3符號分析的基本思路
給定程序的一條執行路徑,我們能推出結果符號的抽象取值。
給定程序的兩條執行路徑,我們得到兩個結果符號的抽象取值 𝑣1,𝑣2,我們可以用如下的操作來合並這兩個值:


如果我們能知道程序所有可能的路徑產生的結果 符號𝑣1,𝑣2,…,我們就知道了程序的最終結果⊓ (𝑣1,𝑣2,… )。
如何知道程序有哪些可能的路徑?
- 近似方案1:忽略掉程序的條件判斷,認為所有分支 都有可能到達 .
如何能遍歷所有可能的路徑?
- 近似方案2:不在路徑末尾做合並,在控制流匯合的 所有位置提前做合並
1.3數據流分析單調框架
目標:通過配置框架的參數,可以導出各種類型 的算法,並保證算法的安全性、終止性、收斂性。
1.3.1名詞解釋
半格(semilattice)
半格是一個二元組(S,⊓),其中S是一個集合,⊓ 是一個交匯運算,並且任意𝑥,𝑦,𝑧 ∈ 𝑆都滿足下 列條件:
- 冪等性idempotence: 𝑥 ⊓ 𝑥 = 𝑥
- 交換性commutativity: 𝑥 ⊓ 𝑦 = 𝑦 ⊓ 𝑥
- 結合性associativity: 𝑥 ⊓ 𝑦 ⊓ 𝑧 = 𝑥 ⊓ (𝑦 ⊓ 𝑧)
- 存在一個最大元⊤,使得𝑥 ⊓ ⊤ = 𝑥
偏序Partial Order
偏序是一個二元組(S, ⊑),其中S是一個集合, ⊑ 是一個定義在S上的二元關系,並且滿足如下性質:
- 自反性:∀𝑎 ∈ 𝑆:𝑎 ⊑ 𝑎
- 傳遞性:∀𝑥,𝑦,𝑧 ∈ 𝑆:𝑥 ⊑ 𝑦 ∧ 𝑦 ⊑ 𝑧 ⇒ 𝑥 ⊑ 𝑧
- 非對稱性:𝑥 ⊑ 𝑦 ∧ 𝑦 ⊑ 𝑥 ⇒ 𝑥 = 𝑦
每個半格都定義了一個偏序關系
- 𝑥 ⊑ 𝑦當且僅當𝑥 ⊓ 𝑦 = 𝑥
1.3.2半格示例
抽象符號域的五個元素和交匯操作組成了一個半格,
半格的笛卡爾乘積(𝑆 × 𝑇,⊓𝑥𝑦)還是半格
任意集合和交集操作組成了一個半格
- 偏序關系為子集關系
- 頂元素為全集
任意集合和並集操作組成了一個半格
- 偏序關系為超集關系
- 頂元素為空集
半格和偏序關系
每個半格都定義了同一集合SSS上的一個偏序關系
例如,正整數集合上的"求最小公倍數運算"是半格,而"整除關系"是對應的偏序。
又如,任意集合和"交集操作"組成了一個半格,頂元素是全集,而"子集關系"是對應的偏序。
又如,任意集合和"並集操作"組成了一個半格,頂元素是空集,而"超集關系"是對應的偏序。
半格的高度
定義: 半格的偏序圖中任意兩個結點 的最大距離+1。
1.3.3單調(遞增)函數 Monotone (Increasing) Function
定義:給定一個偏序關系(𝑆,⊑),稱一個定義在𝑆上的 函數𝑓為單調函數,當且僅當對任意𝑎,𝑏 ∈ 𝑆滿足
- 𝑎 ⊑ 𝑏 ⇒ 𝑓 (𝑎) ⊑ 𝑓 (𝑏)
- 注意:單調不等於a ⊑ 𝑓 (𝑎)
單調函數示例
- 在符號分析的半格中,固定任一輸入參數,抽象符號 的四個操作均為單調函數
- 在集合和交/並操作構成的半格中,給定任意兩個集 合GEN, KILL,函數𝑓 (𝑆) =( 𝑆 − 𝐾𝐼𝐿𝐿) ∪ GEN為單調函 數
1.3.4數據流分析單調框架
- 一個控制流圖(𝑉,𝐸)
- 一個有限高度的半格(𝑆,⊓)
- 一個entry的初值𝐼
- 一組結點轉換函數,對任意𝑣 ∈ 𝑉 − 𝑒𝑛𝑡𝑟𝑦存在 一個結點轉換函數𝑓v
算法偽代碼:
2.數據流分析應用
2.1Reaching Definitions可達定值分析
2.1.1原理
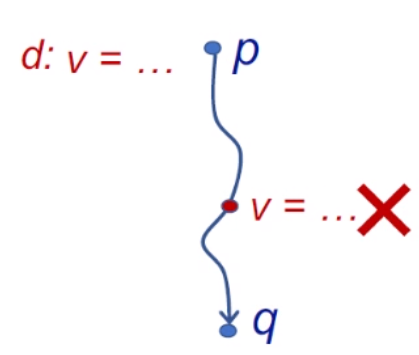
如下圖所示,我們在p點定義了一個變量v,在p到q的路徑中,如果v被重新定義了,那么我們就說這個變量被“殺死了”,如果變量沒有被殺死,那么v的值就可以順利傳導到q點。可達定值分析常常用來判斷某個已經被聲明的變量是否被使用過。
2.1.2分析過程
我們繼續使用Abstract和safe-approximation兩步驟來進行可達定值分析。
-
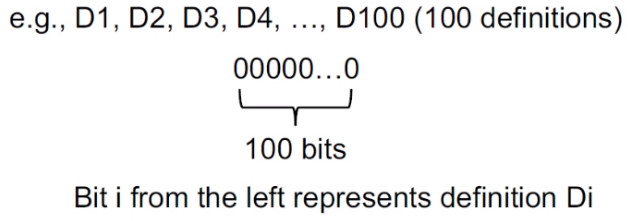
Abstraction:將所定義的每個變量狀態用bit vectors來表示,如下圖所示:
-
Safe-approximation:我們假設有一個聲明D: v = x op y,這條語句新增了一個對於v的聲明,並殺死了所有其他對於v的聲明,語句的其他部分不受影響。轉換函數如下:

一個簡單的實例如下所示:
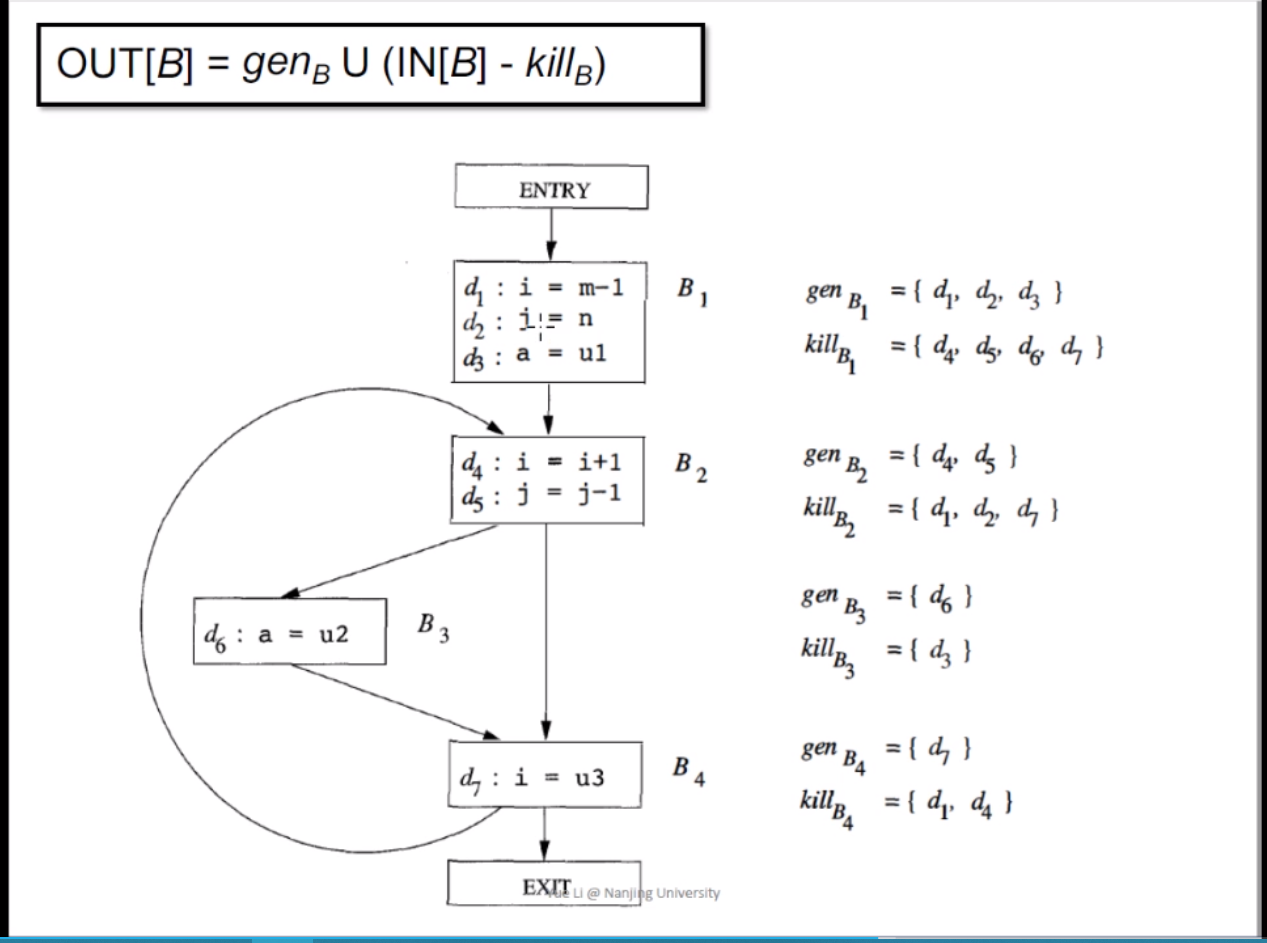
每個基本塊誕生和殺死的聲明如上圖所示,這個很好理解。
2.1.3可達定值分析的偽代碼

我們先將所有BB的輸出設置成空,然后利用我們的轉換函數對於每一個BB的輸入輸出進行迭代,在一次迭代過程中如果有BB的輸出發生變化則進行下一次迭代,直到所有BB的輸出都不變為止。
may analysis一般都初始化為空,must analysis一般都初始化為Top
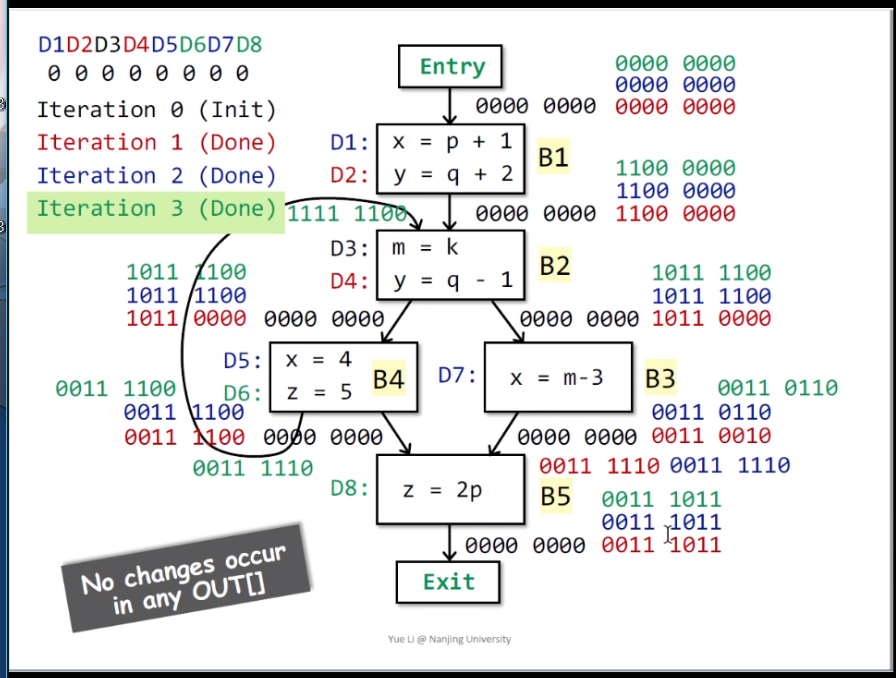
2.1.4可達定值分析實例
如下圖所示是一個可達分析的實例,可以自己試着按照上面的偽代碼做一下分析,看最終的結果是什么。
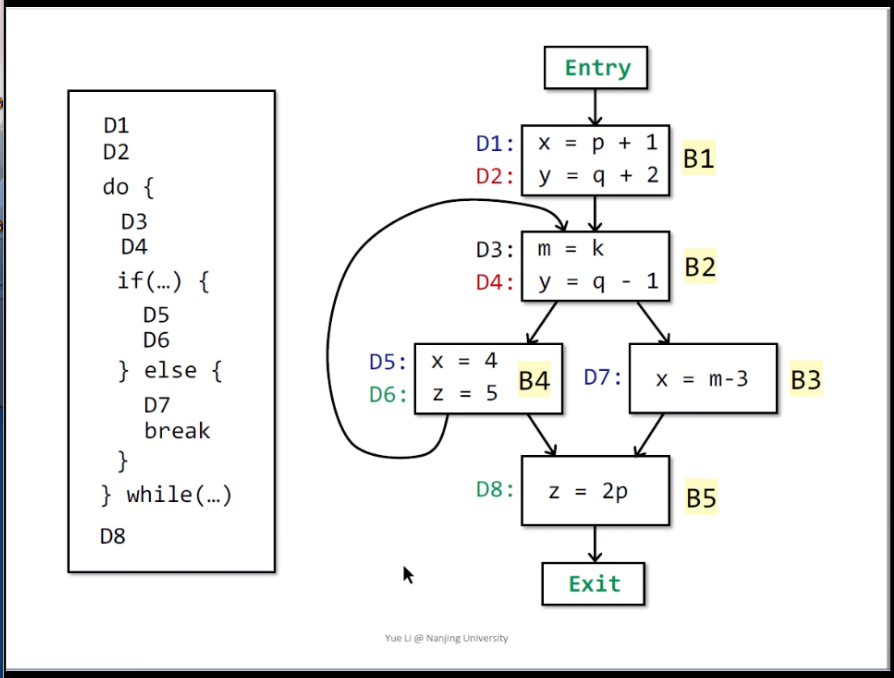
最終結果是: