深度學習中常常會存在過擬合現象,比如當訓練數據過少時,訓練得到的模型很可能在訓練集上表現非常好,但是在測試集上表現不好.
應對過擬合,可以通過數據增強,增大訓練集數量.我們這里先不介紹數據增強,先從模型訓練的角度介紹常用的應對過擬合的方法.
權重衰減
權重衰減等價於 \(L_2\) 范數正則化(regularization)。正則化通過為模型損失函數添加懲罰項使學出的模型參數值較小,是應對過擬合的常用手段。我們先描述\(L_2\)范數正則化,再解釋它為何又稱權重衰減。
\(L_2\)范數正則化在模型原損失函數基礎上添加\(L_2\)范數懲罰項,從而得到訓練所需要最小化的函數。\(L_2\)范數懲罰項指的是模型權重參數每個元素的平方和與一個正的常數的乘積。線性回歸一文中的線性回歸損失函數
為例,其中\(w_1, w_2\)是權重參數,\(b\)是偏差參數,樣本\(i\)的輸入為\(x_1^{(i)}, x_2^{(i)}\),標簽為\(y^{(i)}\),樣本數為\(n\)。將權重參數用向量\(\boldsymbol{w} = [w_1, w_2]\)表示,帶有\(L_2\)范數懲罰項的新損失函數為
其中超參數\(\lambda > 0\)。當權重參數均為0時,懲罰項最小。當\(\lambda\)較大時,懲罰項在損失函數中的比重較大,這通常會使學到的權重參數的元素較接近0。當\(\lambda\)設為0時,懲罰項完全不起作用。上式中\(L_2\)范數平方\(\|\boldsymbol{w}\|^2\)展開后得到\(w_1^2 + w_2^2\)。
顯然,相比沒有正則化項的loss,有了\(L_2\)范數懲罰項后求導后將多出來一項\({\lambda}w_i\),所以,在小批量隨機梯度下降中,權重\(w_1\)和\(w_2\)的迭代方式將變為
可見,\(L_2\)范數正則化令權重\(w_1\)和\(w_2\)先自乘小於1的數,再減去不含懲罰項的梯度。因此,\(L_2\)范數正則化又叫權重衰減.
權重衰減通過懲罰絕對值較大的模型參數為需要學習的模型增加了限制,這可能對過擬合有效。實際場景中,我們有時也在懲罰項中添加偏差元素的平方和。
高維線性回歸實驗
我們創建一個數據集,來模擬過擬合,以及權重衰減針對過擬合的效果.
設數據樣本特征的維度為\(p\)。對於訓練數據集和測試數據集中特征為\(x_1, x_2, \ldots, x_p\)的任一樣本,我們使用如下的線性函數來生成該樣本的標簽:
其中噪聲項\(\epsilon\)服從均值為0、標准差為0.01的正態分布。為了較容易地觀察過擬合,我們考慮高維線性回歸問題,如設維度\(p=200\);同時,我們特意把訓練數據集的樣本數設低,如20。
導入必要的包
import torch
import torch.nn as nn
import numpy as np
數據集創建
n_train, n_test, num_inputs = 20, 100, 200
true_w, true_b = torch.ones(num_inputs, 1) * 0.01, 0.05
features = torch.randn((n_train + n_test, num_inputs))
labels = torch.matmul(features, true_w) + true_b
labels += torch.tensor(np.random.normal(0, 0.01,
size=labels.size()), dtype=torch.float)
train_features, test_features = features[:n_train, :], features[n_train:, :]
train_labels, test_labels = labels[:n_train], labels[n_train:]
dataset = torch.utils.data.TensorDataset(train_features, train_labels)
參數初始化
def init_params():
w = torch.rand((num_inputs, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
return [w, b]
模型定義
def linreg(X, w, b):
# print(X.dtype,b.dtype)
return torch.mm(X, w) + b
損失函數定義
由於我們想驗證L2正則項的作用,所以需要定義l2_penalty(w),loss由2部分構成,一部分就是正常的均方誤差,一部分是
L2正則項,用以控制w的大小. \(\lambda\)則表示這兩部分誤差的比例.
(y_hat - y.view(y_hat.size())) ** 2 / 2是一個shape為[batch,1]的Tensor,(w**2).sum()/2是一個標量,
他們二者相加時,后者會自動擴展成與前者相同shape的張量.
def squared_loss(y_hat, y):
# 注意這里返回的是向量, 另外, pytorch里的MSELoss並沒有除以 2
return (y_hat - y.view(y_hat.size())) ** 2 / 2
def l2_penalty(w):
return (w**2).sum()/2
def total_loss(y_hat, y,w,lambd):
return (y_hat - y.view(y_hat.size())) ** 2 / 2 + lambd * (w**2).sum()/2 #這里用了廣播機制
定義優化器
def sgd(params, lr, batch_size):
for param in params:
param.data -= lr * param.grad / batch_size # 注意這里更改param時用的param.data
訓練
注意,在訓練階段,在反向傳播時,我們計算loss時用的是total_loss,即加入了L2正則項的.在推導階段,計算在訓練集/測試集上的loss
用的是squared_loss.
batch_size, num_epochs, lr = 2, 100, 0.003
train_iter = torch.utils.data.DataLoader(dataset,batch_size=batch_size,shuffle=True)
net = linreg
def train(lamda):
w,b = init_params()
train_ls, test_ls = [], []
for epoch in range(num_epochs):
for X,y in train_iter:
y_hat = net(X,w,b)
l = total_loss(y_hat,y,w,lamda).sum()
#print(w.grad.data)
if w.grad is not None:
#print(w.grad.data)
w.grad.data.zero_()
b.grad.data.zero_()
else:
print("grad 0 epoch %d" % (epoch))
l.backward()
sgd([w,b], lr, batch_size)
#print(l.item())
train_l = squared_loss(net(train_features,w,b),train_labels)
print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))
train_ls.append(train_l.mean().item())
test_l = squared_loss(net(test_features,w,b),test_labels)
print('epoch %d, loss %f' % (epoch + 1, test_l.mean().item()))
test_ls.append(test_l.mean().item())
d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
range(1, num_epochs + 1), test_ls, ['train', 'test'])
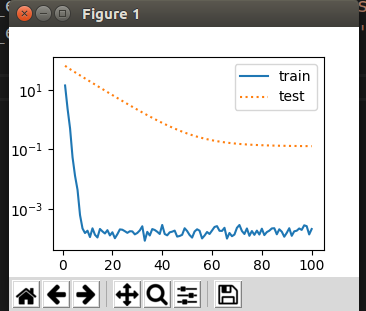
當train(0)時,即相當於不帶正則項的loss.繪制出的曲線如下:

當train(1)時,即相當於squared_loss和L2正則項為1:1,繪制出的曲線如下:

以上是我們手動實現了損失函數,優化器等.用torch里封裝好的MSELoss,optim等實現如下:
def train_use_torch(wd):
net = torch.nn.Linear(num_inputs,1)
loss = nn.MSELoss()
nn.init.normal_(net.weight,mean=0,std=1)
nn.init.normal_(net.bias,mean=0,std=1)
optimizer_w =torch.optim.SGD(params=[net.weight],lr=lr,weight_decay=wd) #權重衰減
optimizer_b =torch.optim.SGD(params=[net.bias],lr=lr) #偏差參數衰減
train_ls, test_ls = [], []
for epoch in range(num_epochs):
for X,y in train_iter:
y_hat = net(X)
l = loss(y_hat,y).sum()
optimizer_w.zero_grad()
optimizer_b.zero_grad()
l.backward()
optimizer_w.step()
optimizer_b.step()
train_l = squared_loss(net(train_features),train_labels)
print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))
train_ls.append(train_l.mean().item())
test_l = squared_loss(net(test_features),test_labels)
print('epoch %d, loss %f' % (epoch + 1, test_l.mean().item()))
test_ls.append(test_l.mean().item())
d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
range(1, num_epochs + 1), test_ls, ['train', 'test'])
對不同的參數,我們用不同的optimizer實例,w需要衰減,b不需要.
optimizer_w =torch.optim.SGD(params=[net.weight],lr=lr,weight_decay=wd) #權重衰減
optimizer_b =torch.optim.SGD(params=[net.bias],lr=lr) #偏差參數衰減
```
同樣的,在更新參數時,需要對兩個optimizer實例都調用
optimizer_w.step()
optimizer_b.step()
最終繪制效果如下: