作者要解決的問題
仍然是one-stage中的一個經典問題,正負、難易樣本不均衡。因為anchor的原因,pos : neg>= 1 : 70。負樣本大多比較簡單,所以也導致了難易樣本的問題。
Focal loss(CVPR2017)
Focal loss的解決方案
傳統的交叉熵損失函數:
\[L_{CE} = -[p^*(log(p) + (1-p^*)log(1-p)] \]
\(p^*=\{0, 1\}\)為真實標簽,\(p \in (0, 1)\)為網絡的預測概率。可以看到,傳統的交叉熵損失函數平等的看待正負樣本。
Focal loss
\[L = -[\alpha p^\gamma p^*log(p) + (1-\alpha)(1-p)^\gamma (1-p^*)log(1-p)] \]
可以看到Focal loss引入了兩個超參數\(\alpha, \gamma\),\(\alpha\)用來平衡正負樣本,\(\gamma\)用來平衡難易樣本。簡單分析一下,加號的左側是正樣本的損失,右側是負樣本的損失。通過乘上不同的系數\((\alpha, 1-\alpha)\),來平衡正負樣本。對於簡單樣本,其loss較小,概率值更接近真實標簽,這樣概率的\(\gamma\)次方越小,相反地,難樣本的就會變大,使難樣本的損失上升,使網絡關注難樣本。
Focal loss的不足
雖然Focal loss這篇論文也在一定程度上解決了正負樣本不均衡的問題,但是Focal loss引入了兩個超參數,調參費勁,且只能應用到box分類上,無法解決回歸的問題。
設計思路
梯度與樣本的關系
作者觀察到難易樣本的分布與梯度有着如下的關系,可以看到,梯度較小時(簡單樣本),樣本數量非常多,梯度適中時,樣本較少。另外值得注意的一點是,梯度在1左右的樣本數量還是不少的。作者將這些樣本視為異常值,解決特別難的樣本會導致其他的樣本准確率下降。
針對以上發現,作者采用梯度分布(梯度附近的樣本數)來處理難易樣本不平衡的問題。簡單思路就是梯度小的樣本數比較大,那就給他們乘上一個小系數,梯度大的樣本少乘以一個大的系數。不過這個系數不是靠自己調的,而是根據樣本的梯度分布來確定的。 ### 梯度分布計算方法:將0-1的梯度切bin,計算每個bin內落入的樣本數量。 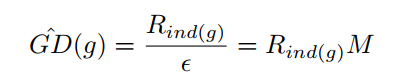 其中$\epsilon$是每個bin的寬度,$M$是$\epsilon$的倒數,表示將0-1切分成多少個bin,$R_{ind(g)}$表示每個bin內落入的樣本數,計算方法如下:
\[R_{ind(g)} = \sum_{k=1}^{N} \delta(g_k,g) \quad \delta(g_k,g) = \begin{cases} 1 \quad if \quad g-\frac{\epsilon}{2} <= g_k <= g+\frac{\epsilon}{2}\\ 0 \quad otherwise \end{cases} \]
\[\beta_i = \frac{N}{GD(g_i)} \]
\(g\)是某點的梯度模,可以理解為以這一點創建一個bin,\(g_k\)是樣本的梯度模,N是樣本總數。
從上面式子可以看到,梯度分布越大,系數越小。
梯度模計算方法
具體的在二分類中,損失函數為上面提到的交叉熵函數
\[L_{CE} = -[p^*(log(p) + (1-p^*)log(1-p)] \\ p=sigmoid(x) \]
對x的梯度
\[\begin{aligned}\frac{\partial L_{CE}}{\partial x} &= \frac{\partial L_{CE}}{\partial p} \times \frac{\partial p}{\partial x}\\&= (-\frac{p^*}{p} + \frac{1-p^*}{1-p}) \times p(1-p)\\&= p-p^*\end{aligned} \]
定義梯度模\(g = |p-p^*|\)
改進
GHM-C損失函數
由此,作者提出分類的損失函數GHM-C
\[L_{GHM-C} = \frac{1}{N}\sum\beta_i L_{CE}(p_i, p_{i}^{*}) \]
還是以這個圖為例,在梯度較小時,樣本數較大,梯度分布$GD(g)$較大,則系數較小,損失較小,這樣就有效的減少了大量簡單樣本的作用。反之亦然。同樣可以分析出特別難的樣本也被抑制了。這一點也是作者希望看到的。 下面這張圖的橫坐標代表原先的梯度分布,縱坐標代表處理后的梯度分布。對比未經任何處理的CE曲線,在0附近的梯度,GHM-C處理后梯度被減小了,0.5左右的樣本梯度被放大了,尤其值得一提的是,對於前面提到的異常樣本,梯度同樣被抑制了。對比Focal loss曲線,明顯可以看出GHM-C更加優秀。
#### GHM-R損失函數 按理說像之前一樣求下梯度分布就好了,不過這里有一個問題。 對於邊框回歸的傳統損失函數smooth_L1
求梯度模 $d= t_i - t_i^*$
可以看到,當$d>\delta$時,梯度模橫為1,無法衡量樣本的難易程度。所以作者這里改了一下
d比較小的時候,類似於$L_2$,d較大時候類似$L_2$,和$SL_1$類似。最終的損失函數如下:
注意一點:回歸的損失函數是只計算正樣本的。 ## 最終結果 COCO數據集上的比較
只有GHM-C的比較
只有GHM-R的比較










