機器學習-線性回歸
本文代碼均來自於《機器學習實戰》
分類算法先說到這里,接下來說一個回歸算法
線性回歸
線性回歸比較簡單,就不怎么說了,要是模型記不得了就百度一下吧,這里列一下公式就直接上代碼了

'''
Created on Jan 8, 2011
@author: Peter
'''
from numpy import *
#加載數據
def loadDataSet(fileName): #general function to parse tab -delimited floats
#attribute的個數
numFeat = len(open(fileName).readline().split('\t')) - 1 #get number of fields
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr =[]
curLine = line.strip().split('\t')
for i in range(numFeat):
lineArr.append(float(curLine[i]))
#dataMat是一個二維矩陣,labelMat是一維的
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
return dataMat,labelMat
#就是,簡單的線性回歸
def standRegres(xArr,yArr):
#這里沒有出現為特征X加1列,因為它已經寫在數據中了2333,要是數據中沒有的話是要寫的。
xMat = mat(xArr); yMat = mat(yArr).T
xTx = xMat.T*xMat#這個是X的轉置乘以X
if linalg.det(xTx) == 0.0:
print("This matrix is singular, cannot do inverse")
return
#.I在numpy中是求逆矩陣
ws = xTx.I * (xMat.T*yMat)
return ws
線性回歸的一個問題就是可能會出現欠擬合現象,因為它求的是具有最小均方誤差的無偏估計,所以如果模型欠擬合的話將不能得到最好的預測效果.所以有些方法允許在估計中引如一些偏差,從而降低預測的均方誤差。其中一個方法就是局部加權線性回歸
---來源當然是《機器學習實戰》
局部加權線性回歸
這頁書中干貨比較多,就直接放上來了
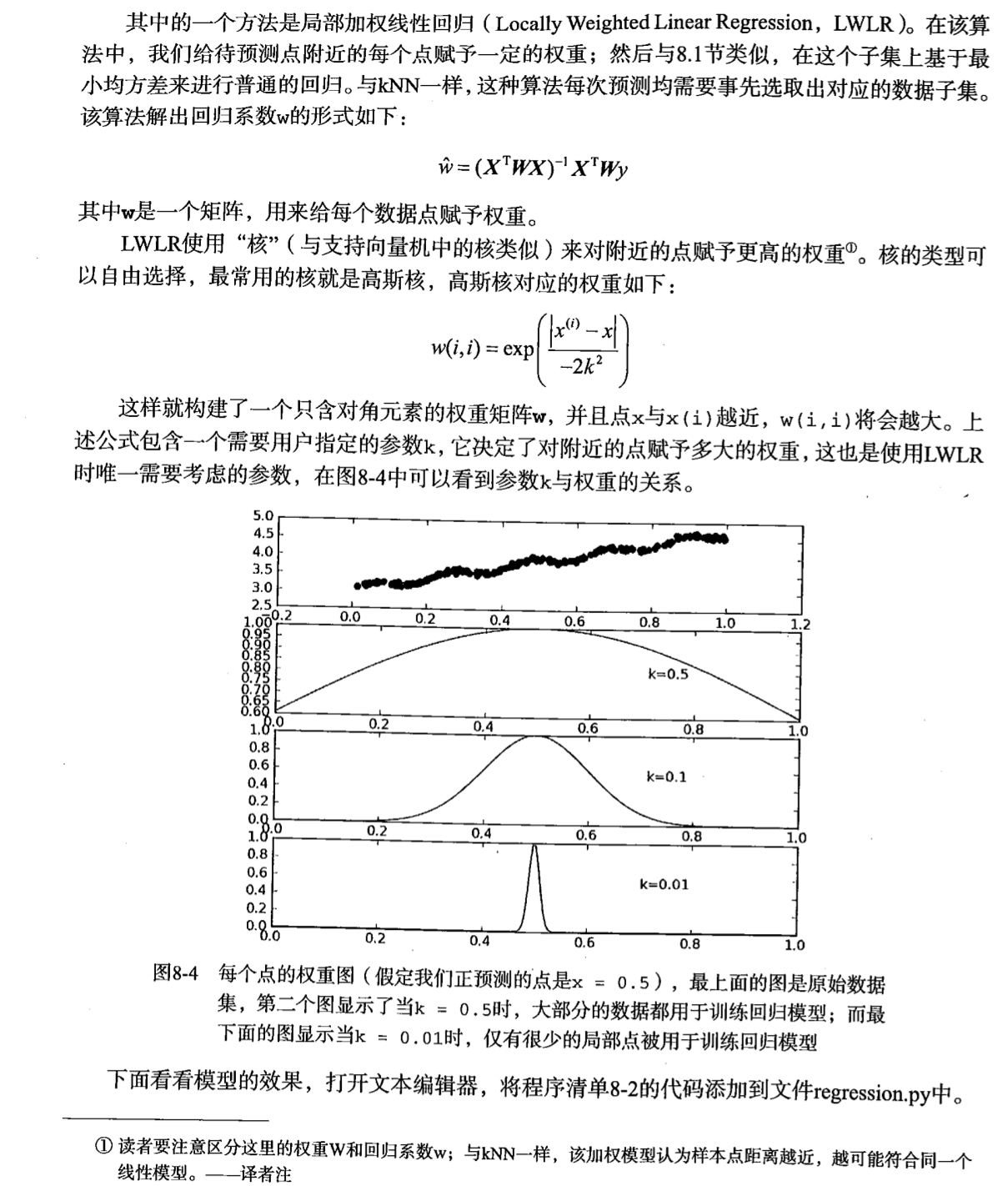
看見沒,人家是用了核函數的,和你們印象中那個傻白甜的線性回歸不一樣!知道書里為什么把它放在SVM后面了吧
那么這個局部加權線性回歸是何方神聖呢?看到網上一個比較靠譜的博客,摘錄如下:
來源:http://cynhard.com/2018/07/13/ML-Locally-Weighted-Linear-Regression/
(由於這位博主用了插件來顯示公式,我就偷懶截圖了2333)
可以看到,所謂“加權”不是直接加在直線方程上的,而是加在損失函數上、用來使函數“跑偏”的。
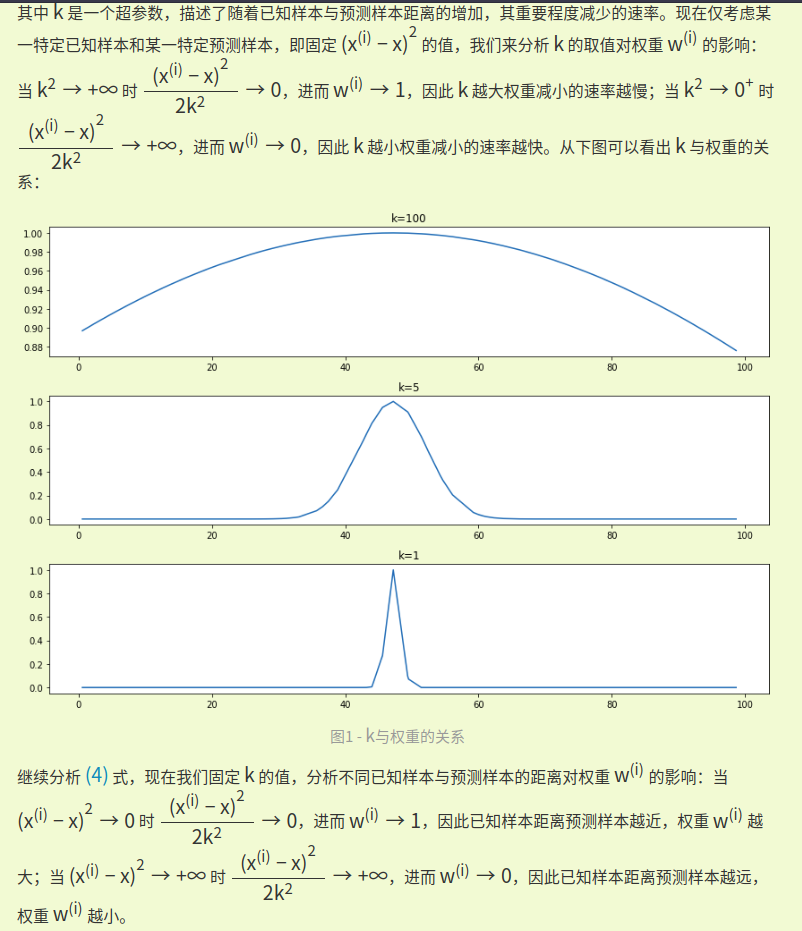
划重點:已知樣本距離預測樣本越近,權重越大;k越大,權重隨距離減小的速度越慢。
局部加權回歸是基於非參數學習算法的思想,使得特征的選擇更好。賦予預測點附近每一個點以一定的權值,在這上面基於波長函數來進行普通的線性回歸.可以實現對臨近點的精確擬合同時忽略那些距離較遠的點的貢獻,即近點的權值大,遠點的權值小,k為波長參數,控制了權值隨距離下降的速度,越大下降的越快。越小越精確並且太小可能出現過擬合的問題。
算法的缺點主要在於對於每一個需要預測的點,都要重新依據整個數據集模擬出一個線性回歸模型出來,使得算法的代價極高。————————————————
版權聲明:本文為CSDN博主「美麗突然發生」的原創文章,遵循 CC 4.0 BY-SA 版權協議,轉載請附上原文出處鏈接及本聲明。
原文鏈接:https://blog.csdn.net/tianse12/article/details/70161591
局部加權線性回歸是不需要“學習”的,屬於和KNN一樣的性質,這點性質甚至還不如線性回歸
代碼如下:
'''
Created on Jan 8, 2011
@author: Peter
'''
from numpy import *
#局部加權線性回歸,需要手動選擇一個合適的k
#輸入的是一個向量而不是矩陣,它一次只能處理一個預測!有點撈
def lwlr(testPoint,xArr,yArr,k=1.0):
#x和y是訓練集樣本
xMat = mat(xArr); yMat = mat(yArr).T
#m是樣本個數
m = shape(xMat)[0]
#創建一個對角單位矩陣用來保存權重w
#使用矩陣而不是向量的原因是為了最后用矩陣乘法好算,公式里面也是這樣寫的
weights = mat(eye((m)))
for j in range(m): #next 2 lines create weights matrix
#一個樣本計算一遍,填到weight中
diffMat = testPoint - xMat[j,:] #
weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2))
xTx = xMat.T * (weights * xMat)
if linalg.det(xTx) == 0.0:
print ("This matrix is singular, cannot do inverse")
return
ws = xTx.I * (xMat.T * (weights * yMat))
return testPoint * ws
#對多個待回歸點進行回歸
def lwlrTest(testArr,xArr,yArr,k=1.0): #loops over all the data points and applies lwlr to each one
m = shape(testArr)[0]
yHat = zeros(m)
for i in range(m):
yHat[i] = lwlr(testArr[i],xArr,yArr,k)
return yHat
#輸出x和y坐標,比lwlrTest更方便將結果畫出來
def lwlrTestPlot(xArr,yArr,k=1.0): #same thing as lwlrTest except it sorts X first
yHat = zeros(shape(yArr)) #easier for plotting
xCopy = mat(xArr)
xCopy.sort(0)#按第一個特征排個序
for i in range(shape(xArr)[0]):
yHat[i] = lwlr(xCopy[i],xArr,yArr,k)
return yHat,xCopy