分析一次double強轉float的翻車原因

背景

人逢喜事精神爽,總算熬到下班撩~~
正准備和同事打個招呼回家,被同事拖住問了.
🙋‍♂️: 你們組做的那塊代碼,把double類型數據成float有問題啊💨.
💁‍♀️: 嗯?不對是正常啊,float精度是沒有double高,但float能保存到小數點后好多位,對我們來說完全夠用了!
🙋‍♂️: 不是啊,這不是小數點多少位的問題,而是現在整型數據,轉出來也有問題啊,你看.

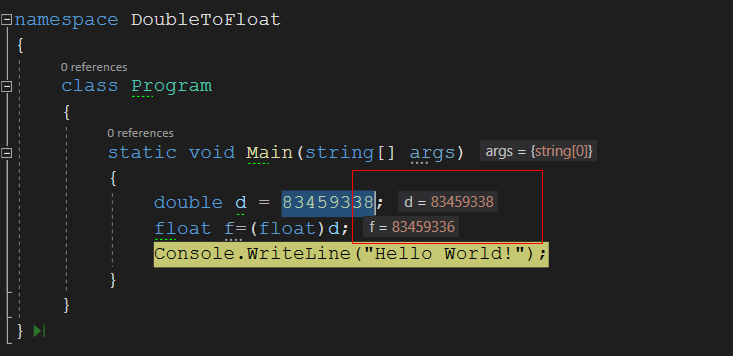
💁‍♀️: XX00😱.... 這什么鬼?

看到這個結果,差點閃到我的老腰🤦,咋不按套路出牌呢?
然后,下班路上,感覺我好像被我摯愛的.Net欺騙了💔,double強轉float用了這么多年,咋說不對就不對了?.Net不靠譜啊!

浮點類型數據的存儲

當然,我內心還是相信.Net是清白的,所以刨根究底,網上找的資料大多是說這種強轉會照成小數點后的精度的問題,可是造成整數位的問題精度問題卻少有人提及.
為了理解這個問題,我們要從一些大學計算機基礎的相關知識講起😂.

float和double有什么不同?

1. float四個字節,double八個字節.
2. float范圍從10^-38到1038 和 -10^38到-10-38, double的范圍從10^-308到10308 和 -10^-308到-10-308

當然了,這都是廢話🤷, 重點是下面這條.

3. float是單精度浮點數,double是雙精度浮點數.

單精度與雙精度什么區別

根據國際標准IEEE 754，任意一個二進制浮點數V可以表示成下面的形式：

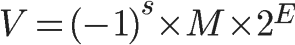
• (-1)^s表示符號位，當s=0，V為正數；當s=1，V為負數。

• M表示有效數字，大於等於1，小於2。

• 2^E表示指數位。

舉例來說，十進制的5.0，寫成二進制是101.0，相當於1.01×2^2。那么，按照上面V的格式，可以得出s=0，M=1.01，E=2。

十進制的-5.0，寫成二進制是-101.0，相當於-1.01×2^2。那么，s=1，M=1.01，E=2。

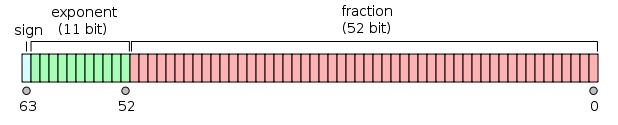
對於32位的單精度浮點數，最高的1位是符號位s，接着的8位是指數E，剩下的23位為有效數字M。

對於64位的雙精度浮點數，最高的1位是符號位S，接着的11位是指數E，剩下的52位為有效數字M。

經過上面關於浮點數的介紹,相信你可能還是一頭霧水,就像下面這幅漫畫展示的那樣🐎.

浮點數轉成內存存儲

為了避免產生上面那種畫馬的跳躍,我們一小步一小步,看看浮點數據具體怎么在內存中存儲的.雙精度與單精度類似,這里我以單精度為例.

1. 先將這個實數的絕對值化為二進制格式。
2. 將這個二進制格式實數的小數點左移或右移n位，直到小數點移動到第一個有效數字的右邊。
3. 從小數點右邊第一位開始數出二十三位數字放入第22到第0位。
4. 如果實數是正的，則在第31位放入“0”，否則放入“1”。
5. ⭐如果n 是左移得到的，說明指數是正的，第30位放入“1”。如果n是右移得到的或n=0，則第30位放入“0”。
6. 如果n是左移得到的，則將n減去1后化為二進制，並在左邊加“0”補足七位，放入第29到第23位。如果n是右移得到的或n=0，則將n化為二進制后在左邊加“0”補足七位，再各位求反，再放入第29到第23位。

我們先用上述步驟嘗試把9.0轉化成二進制存儲形式.

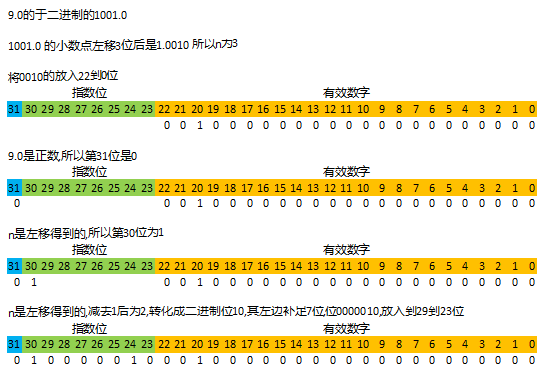
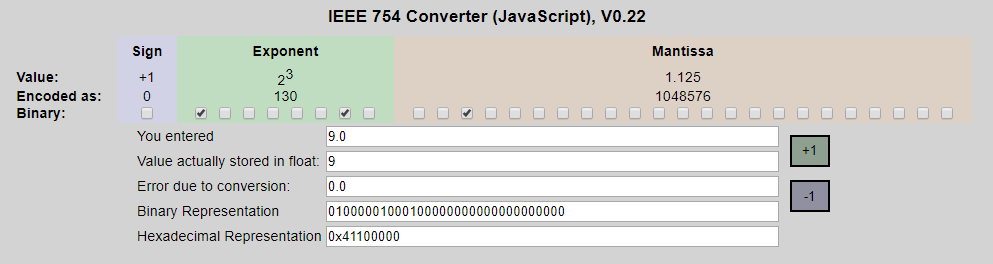
我們可以通過這個地址校驗計算結果的正確性. https://www.h-schmidt.net/FloatConverter/IEEE754.html
可以看到,與我們的計算結果完全一致.

翻車分析

現在我們用上面的步驟,把照成翻車的83459338轉成內存存儲形式看看.

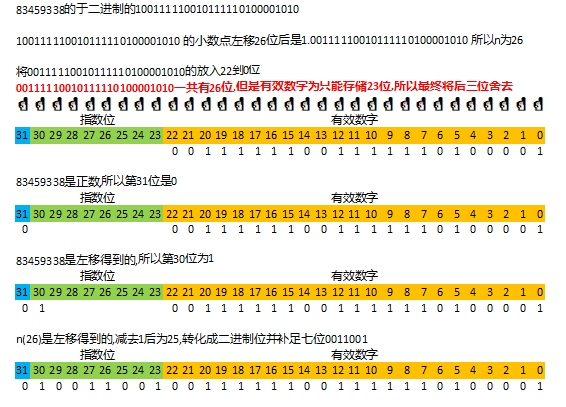
通過在線工具轉換后證實我們的轉換完全正確.

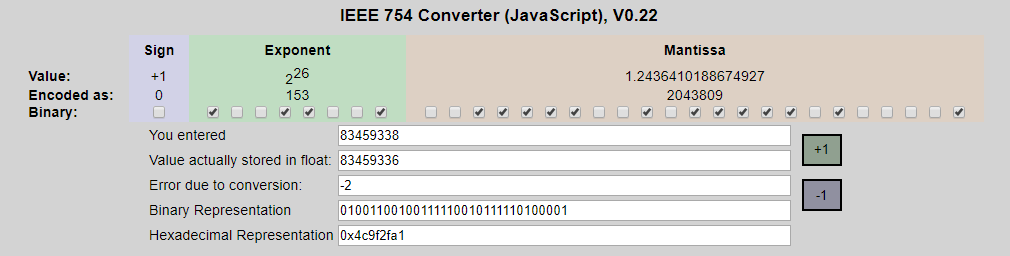
然后我們再把數據轉回來.

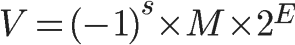
S是第31位,為0, E =0011001(25)+1=26, 重點在M,它是1.(有效數字位)即 1.00111110010111110100001

1.00111110010111110100001乘上2的26次方,為100111110010111110100001000,將其轉換為十進制,為 83459336

沒錯,就是83459336,而不是83459338🌋
83459338=> 100111110010111110100001010
83459336=> 100111110010111110100001000
可以看到,兩個數字轉成成二進制后,倒數第二位產生了差異,而產生這種的差異的原因就是單精度浮點數小數位23位不足以存儲所有二進制數(26位).
🚑這場事故告訴我們,強轉雖好,容易翻車.