引入
填表法,是DP最常見的做法。
以未知的量為基礎,通過已知的量來刷新當前的未知量。
簡介
這是DP最基礎的做法。通常,我們大多題目都可以用這種方法實現。
思路
大致思路

例題
楊輝三角
Description
楊輝三角是二項式系數在三角形中的一種幾何排列。它的每個數等於它上方兩數之和,每行數字左右對稱,由 1 開始逐漸變大。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
請求出楊輝三角的第 n 行,第 m 項的數字是什么。
Input
第一行輸入兩個整數 n,m代表行數和列數。(1≤n,m≤50)
Output
輸出一個整數,代表楊輝三角的第 n 行,第 m項的數字。
Sample Input 1
6 3
Sample Output 1
10
講解
楊輝三角,本質上和我們講的填表法很像(做法就是經典的填表法)。
1. 整理題目的圖
2.楊輝三角的求法
求這個出楊輝三角的坐標為(n,m)的數字是什么,應該找它上兩個的數。
這就是填表法的標志,我們程序就可以用填表法來寫。
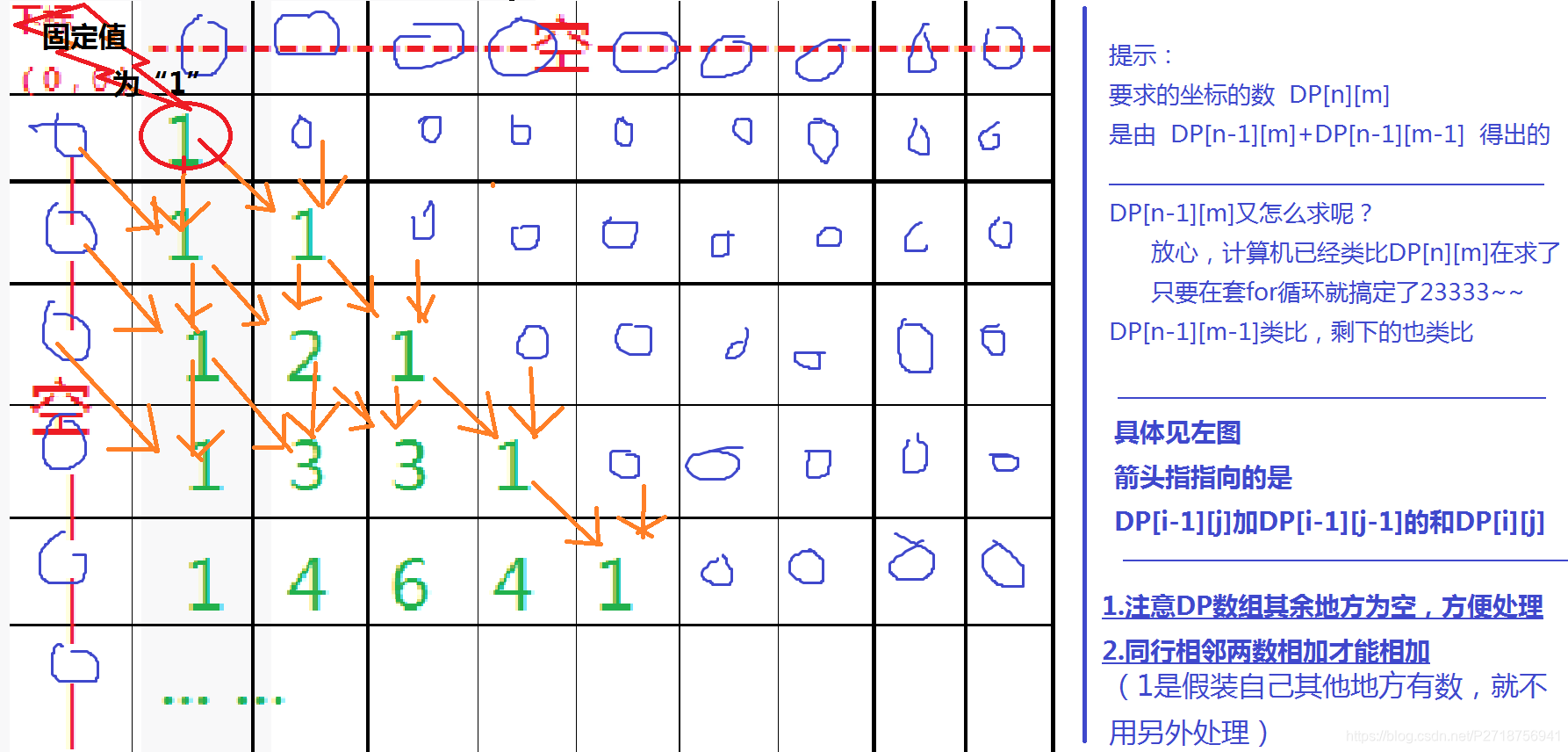
領悟到填表法的精髓了吧?
相信聰明的你,一定能夠自己寫代碼了呢!
例題代碼
#include<bits/stdc++.h>
using namespace std;
int DP[1010][1010];
int n,m;
int main(){
DP[0][0]=1;
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
DP[i][j]=DP[i-1][j]+DP[i-1][j-1];
}
}
cout<<DP[n][m];
return 0;
}
