向面試官一句話解釋卡爾曼濾波:
- 用上一次的最優狀態估計和最優估計誤差去計算這一次的先驗狀態估計和先驗誤差估計;
- 用1得到的本次先驗誤差估計和測量噪聲,得到卡爾曼增益;
- 用1,2步驟得到所有先驗誤差估計和測量噪聲,得到本次的最優估計。
一句話解釋:對模型的預測值和實際的觀測值進行加權,迭代計算出未來的狀態。
對於上面三句話的一些解釋:
- 先驗:根據以往的結果去推導
- 后驗:得到當前結果之后再去修正
- 卡爾曼增益作用:將“粗略估計”變成“最准確的估計”
卡爾曼濾波解決的根本問題:如何讓噪聲的干擾最小(噪聲:可以理解為 實際值-預測值 最小)
卡爾曼濾波的本質:參數化的貝葉斯模型
算法核心思想:根據當前的儀器“測量值”和上一刻的“預測值”和“誤差”,計算得到當前的最優量,再預測下一刻的量。
為什么稱卡爾曼濾波:首先,是卡爾曼本人提出來的;其次,輸出變量都是輸入變量的線性組合,所以可以看做是一種濾波算法。
卡爾曼濾波器可以從最小均方誤差的角度推導出,也可以從貝葉斯推斷的角度來推導。
下面從最小均方誤差的角度推導卡爾曼濾波。
基礎背景知識
卡爾曼的核心:預測+反饋
觀測數據:代表傳感器采集的實際數據,可能存在或多或少的誤差
最優估計:算法計算出來接近於真實值的估計
均方誤差:誤差(每個估計值與真實值的差)的平方,再求和,再求平均。多樣本時,均方誤差等於每個樣本的誤差平方乘以該樣本出現的概率,再求和。
方差:描述隨機變量的離散程度,具體來說是變量值離期望值的距離。

最小均方誤差估計:估計參數,使得估計出來的模型和真實值之間的誤差平方期望最小。
兩個變量之間的協方差: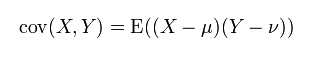
x==y,就是方差。在協方差矩陣中,對角線元素即為方差。x, y都大於期望,協方差為正直;相應自行分析。
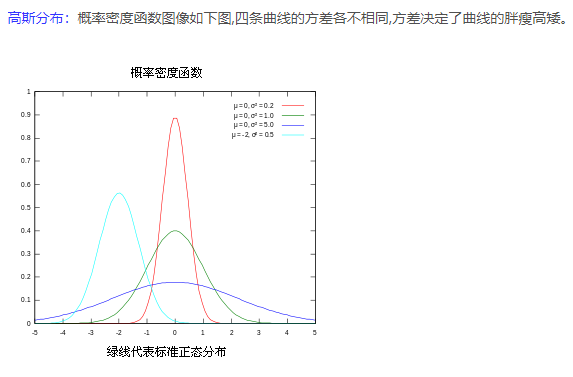
卡爾曼濾波核心公式及解釋


V(k)為測量噪聲
Z(K)為K時刻的測量值
python-opencv 中的kalman濾波模塊
應用重點說明:
A: 轉移矩陣
B: 控制矩陣
H:測量矩陣
一維中的卡爾曼濾波實現(注重原理的理解)
import numpy as np
import matplotlib.pyplot as plt
#這里是假設A=1,H=1, B=0的情況
# 故動態模型 X(k) = X(k-1) + 噪聲
# Z(K) = X(k)
# 動態模型是一個常量
# intial parameters
n_iter = 50
sz = (n_iter,) # size of array
x = -0.37727 # truth value (typo in example at top of p. 13 calls this z)
z = np.random.normal(x,0.1,size=sz) # observations (normal about x, sigma=0.1)
Q = 1e-5 # process variance
# allocate space for arrays
xhat=np.zeros(sz) # a posteri estimate of x
P=np.zeros(sz) # a posteri error estimate
xhatminus=np.zeros(sz) # a priori estimate of x
Pminus=np.zeros(sz) # a priori error estimate
K=np.zeros(sz) # gain or blending factor
R = 0.1**2 # estimate of measurement variance, change to see effect
# intial guesses
xhat[0] = 0.0
P[0] = 1.0
for k in range(1,n_iter):
# time update
xhatminus[k] = xhat[k-1] #X(k|k-1) = AX(k-1|k-1) + BU(k) + W(k),A=1,BU(k) = 0
Pminus[k] = P[k-1]+Q #P(k|k-1) = AP(k-1|k-1)A' + Q(k) ,A=1
# measurement update
K[k] = Pminus[k]/( Pminus[k]+R ) #Kg(k)=P(k|k-1)H'/[HP(k|k-1)H' + R],H=1
xhat[k] = xhatminus[k]+K[k]*(z[k]-xhatminus[k]) #X(k|k) = X(k|k-1) + Kg(k)[Z(k) - HX(k|k-1)], H=1
P[k] = (1-K[k])*Pminus[k] #P(k|k) = (1 - Kg(k)H)P(k|k-1), H=1
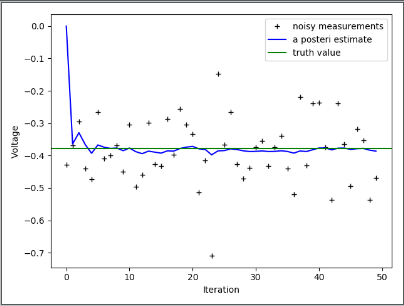
plt.figure()
plt.plot(z, 'k+', label='noisy measurements') # 測量值
plt.plot(xhat, 'b-', label='a posteri estimate') # 過濾后的值
plt.axhline(x, color='g', label='truth value') # 系統值
plt.legend()
plt.xlabel('Iteration')
plt.ylabel('Voltage')
plt.show()