區塊鏈中的密碼學之默克爾樹(十五)

本文轉載自查看原文 2019-04-10 22:48 723 區塊鏈/ 密碼學

1. 前言
2. 默克爾樹
3. 布隆過濾器
4. 同態加密
- 4.1 概覽：同態加密的概念
- 4.2 同態加密的定義、安全性和簡單實例
5. 零知識證明

1. 前言

2. 默克爾樹

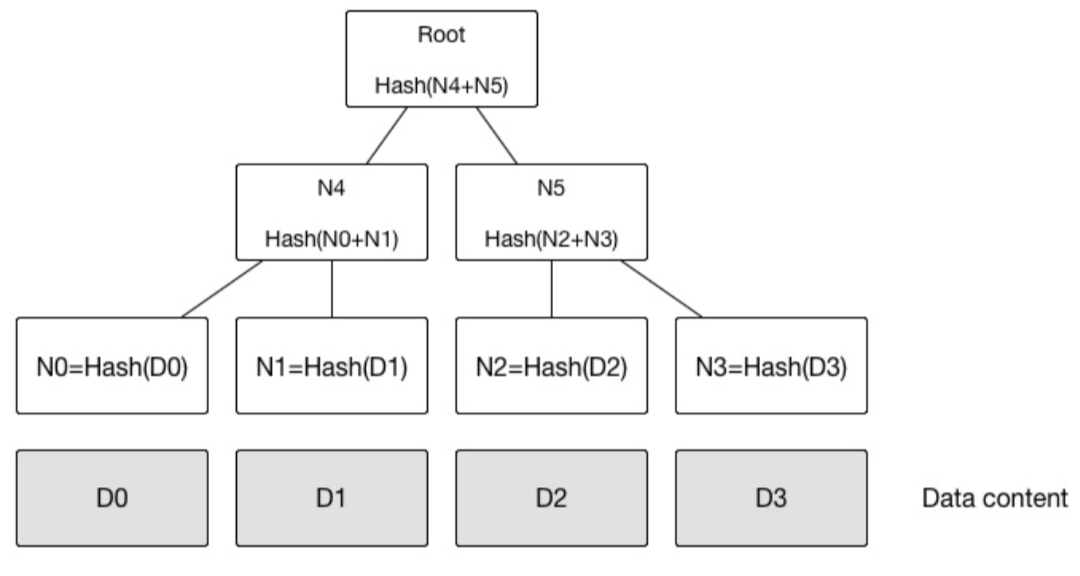
默克爾樹（又叫哈希樹）是一種二叉樹，由一個根節點、一組中間節點和一組葉節點組成。最下面的葉節點包含存儲數據或其哈希值，每個中間節點是它的兩個孩子節點內容的哈希值，根節點也是由它的兩個子節點內容的哈希值組成。

進一步的，默克爾樹可以推廣到多叉樹的情形。
默克爾樹的特點是，底層數據的任何變動，都會傳遞到其父親節點，一直到樹根。
默克爾樹的典型應用場景包括：

快速比較大量數據：當兩個默克爾樹根相同時，則意味着所代表的數據必然相同。
快速定位修改：例如上例中，如果 D1 中數據被修改，會影響到 N1，N4 和 Root。因此，沿着 Root --> N4 --> N1，可以快速定位到發生改變的 D1；時間復雜度為O(logn)
零知識證明：例如如何證明某個數據（ D0……D3）中包括給定內容 D0，很簡單，構造一個默克爾樹，公布 N0，N1，N4，Root，D0 擁有者可以很容易檢測 D0 存在，但不知道其它內容。

默克爾樹的查找的時間復雜度為O（logn）。對於Merkle Tree數據塊的更新操作其實是很簡單的，更新完數據塊，然后接着更新其到樹根路徑上的Hash值就可以了，這樣不會改變Merkle Tree的結構。

3. 布隆過濾器

布隆過濾器是一種基於Hash的高效查找結構，能夠快速（常數時間內）回答“某個元素是否在一個集合內”的問題。

其本質上是利用了hash算法的查找的時間復雜度為O(1)，但其缺點是空間復雜度過高，空間利用率太低，一般不會超過50%，Bloom Filter進行了折中，即使用了多個hash函數，大大降低了空間復雜度，於此同時，時間復雜度也基本不變。但其也是有代價的，其不是精確匹配的，於此相比，hash表則是精確匹配的，所以任何事情都是有代價的。

什么情況下需要布隆過濾器？

先來看幾個比較常見的例子

字處理軟件中，需要檢查一個英語單詞是否拼寫正確
在 FBI，一個嫌疑人的名字是否已經在嫌疑名單上
在網絡爬蟲里，一個網址是否被訪問過
yahoo, gmail等郵箱垃圾郵件過濾功能

這幾個例子有一個共同的特點： 如何判斷一個元素是否存在一個集合中？

常規思路

數組
鏈表
樹、平衡二叉樹、Trie
Map (紅黑樹)
哈希表

雖然上面描述的這幾種數據結構配合常見的排序、二分搜索可以快速高效的處理絕大部分判斷元素是否存在集合中的需求。但是當集合里面的元素數量足夠大，如果有500萬條記錄甚至1億條記錄呢？這個時候常規的數據結構的問題就凸顯出來了。數組、鏈表、樹等數據結構會存儲元素的內容，一旦數據量過大，消耗的內存也會呈現線性增長，最終達到瓶頸。有的同學可能會問，哈希表不是效率很高嗎？查詢效率可以達到O(1)。但是哈希表需要消耗的內存依然很高。使用哈希表存儲一億個垃圾 email 地址的消耗？哈希表的做法：首先，哈希函數將一個email地址映射成8字節信息指紋；考慮到哈希表存儲效率通常小於50%（哈希沖突）；因此消耗的內存：8 * 2 * 1億字節 = 1.6G 內存，普通計算機是無法提供如此大的內存。這個時候，布隆過濾器（Bloom Filter）就應運而生。

布隆過濾器介紹

巴頓.布隆於一九七零年提出，一個很長的二進制向量（位數組），一系列隨機函數 (哈希)，空間效率和查詢效率高，有一定的誤判率（哈希表是精確匹配）。

布隆過濾器原理

布隆過濾器（Bloom Filter）的核心實現是一個超大的位數組和幾個哈希函數。假設位數組的長度為m，哈希函數的個數為k

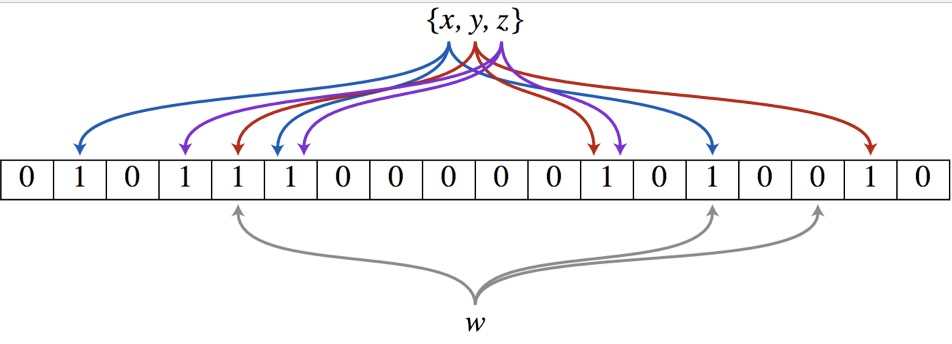
以上圖為例，具體的操作流程：假設集合里面有3個元素{x, y, z}，哈希函數的個數為3。首先將位數組進行初始化，將里面每個位都設置位0。對於集合里面的每一個元素，將元素依次通過3個哈希函數進行映射，每次映射都會產生一個哈希值，這個值對應位數組上面的一個點，然后將位數組對應的位置標記為1。查詢W元素是否存在集合中的時候，同樣的方法將W通過哈希映射到位數組上的3個點。如果3個點的其中有一個點不為1，則可以判斷該元素一定不存在集合中。反之，如果3個點都為1，則該元素可能存在集合中。注意：此處不能判斷該元素是否一定存在集合中，可能存在一定的誤判率。可以從圖中可以看到：假設某個元素通過映射對應下標為4，5，6這3個點。雖然這3個點都為1，但是很明顯這3個點是不同元素經過哈希得到的位置，因此這種情況說明元素雖然不在集合中，也可能對應的都是1，這是誤判率存在的原因。

布隆過濾器添加元素

將要添加的元素給k個哈希函數
得到對應於位數組上的k個位置
將這k個位置設為1

布隆過濾器查詢元素

將要查詢的元素給k個哈希函數
得到對應於位數組上的k個位置
如果k個位置有一個為0，則肯定不在集合中
如果k個位置全部為1，則可能在集合中

4. 同態加密

鏈接：https://www.zhihu.com/question/27645858/answer/37598506

4.1 概覽：同態加密的概念

同態加密（Homomorphic Encryption）是很久以前密碼學界就提出來的一個Open Problem。早在1978年，Ron Rivest, Leonard Adleman, 以及Michael L. Dertouzos就以銀行為應用背景提出了這個概念[RAD78]。對，你沒有看錯，Ron Rivest和Leonard Adleman分別就是著名的RSA算法中的R和A。至於中間的S，Adi Shamir，現在仍然在為密碼學貢獻新的工作。

什么是同態加密？

提出第一個構造出全同態加密（Fully Homomorphic Encryption）[Gen09]的Craig Gentry給出的直觀定義最好：

A way to delegate processing of your data, without giving away access to it.

這是什么意思呢？一般的加密方案關注的都是數據存儲安全。即，我要給其他人發個加密的東西，或者要在計算機或者其他服務器上存一個東西，我要對數據進行加密后在發送或者存儲。沒有密鑰的用戶，不可能從加密結果中得到有關原始數據的任何信息。只有擁有密鑰的用戶才能夠正確解密，得到原始的內容。我們注意到，這個過程中用戶是不能對加密結果做任何操作的，只能進行存儲、傳輸。對加密結果做任何操作，都將會導致錯誤的解密，甚至解密失敗。

同態加密方案最有趣的地方在於，其關注的是數據處理安全。同態加密提供了一種對加密數據進行處理的功能。也就是說，其他人可以對加密數據進行處理，但是處理過程不會泄露任何原始內容。同時，擁有密鑰的用戶對處理過的數據進行解密后，得到的正好是處理后的結果。

有點抽象？我們舉個實際生活中的例子。有個叫Alice的用戶買到了一大塊金子，她想讓工人把這塊金子打造成一個項鏈。但是工人在打造的過程中有可能會偷金子啊，畢竟就是一克金子也值很多錢的說… 因此能不能有一種方法，讓工人可以對金塊進行加工（delegate processing of your data），但是不能得到任何金子（without giving away access to it）？當然有辦法啦，Alice可以這么做：

Alice將金子鎖在一個密閉的盒子里面，這個盒子安裝了一個手套。
工人可以帶着這個手套，對盒子內部的金子進行處理。但是盒子是鎖着的，所以工人不僅拿不到金塊，連處理過程中掉下的任何金子都拿不到。
加工完成后。Alice拿回這個盒子，把鎖打開，就得到了金子。

這個盒子的樣子大概是這樣的：

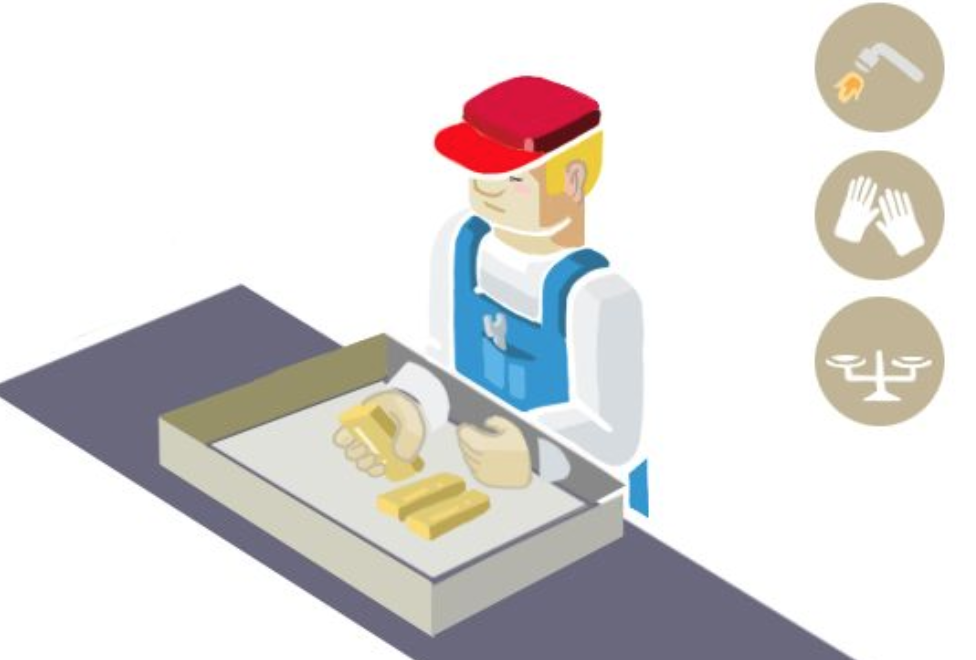
這里面的對應關系是：

盒子：加密算法
盒子上的鎖：用戶密鑰
將金塊放在盒子里面並且用鎖鎖上：將數據用同態加密方案進行加密
加工：應用同態特性，在無法取得數據的條件下直接對加密結果進行處理
開鎖：對結果進行解密，直接得到處理后的結果

同態加密哪里能用？

這幾年不是提了個雲計算的概念嘛。同態加密幾乎就是為雲計算而量身打造的！我們考慮下面的情景：一個用戶想要處理一個數據，但是他的計算機計算能力較弱。這個用戶可以使用雲計算的概念，讓雲來幫助他進行處理而得到結果。但是如果直接將數據交給雲，無法保證安全性啊！於是，他可以使用同態加密，然后讓雲來對加密數據進行直接處理，並將處理結果返回給他。這樣一來：

用戶向雲服務商付款，得到了處理的結果；
雲服務商掙到了費用，並在不知道用戶數據的前提下正確處理了數據；

這方法簡直完美啊有沒有？！但是，這么好的特性肯定會帶來一些缺點。同態加密現在最需要解決的問題在於：效率。效率一詞包含兩個方面，一個是加密數據的處理速度，一個是這個加密方案的數據存儲量。我們可以直觀地想一想這個問題：

工人戴着手套加工金子，肯定沒有直接加工來得快嘛~ 也就是說，隔着手套處理，精准度會變差（現有構造會有誤差傳遞問題），加工的時間也會變得更長（密文的操作花費更長的時間），工人需要隔着操作，因此也需要更專業（會正確調用算法）。
金子放在盒子里面，為了操作，總得做一個稍微大一點的盒子吧，要不然手操作不開啊（存儲空間問題）。里面也要放各種工具吧，什么電鑽啦，銼刀啦，也需要空間吧？

這種加密方案真的有在研究？

我舉3個簡單的例子：

第一個構造出全同態加密方案的人是Gentry，這是他在Stanford攻讀博士學位的研究成果。Gentry畢業后去哪里了呢？IBM。大家知道IBM可是一個雲服務提供商啊！在IBM，Gentry和另一個密碼學大牛Halevi繼續進行同態加密及其相關的研究，並實現了一些同態加密方案。如果IBM真的做出了可以在實際使用的同態加密方案，那么其他雲服務提供商就可以拜拜了啊！這游戲不用玩了啊，人家能在不知道數據內容得前提下處理數據啊，畢竟誰都不想把數據泄露給其他公司啊！
國內的某個大公司（具體是哪個我就不透露了…）對這方面的研究非常感興趣，我也和他們做了一次交流，並且初步達成了一定的研究大方向。要不怎么我現在也去弄這個頭大的東西呢。要知道，國內的公司也沒閑着，這是制高點，拿到了就是一家獨大，而且是超級技術壟斷，不公開源代碼或者不了解內部構造的話想仿造都仿造不了啊…不過，這方面的研究說實話Gap確實大，入門起碼要3個月的時間，還不一定做的出來…
即使沒有實現全同態加密，也可以得到其他一些很有趣的結論。而每一個結論都可能引發技術壟斷。這些結論由於涉及到了一定的基礎知識，我在后面中會進行介紹。

業界如何評價全同態加密的構造？

在此引用一個前輩的話：

如果未來真的做出了Practical Fully Homomorphic Encryption，那么Gentry一定可以得到圖靈獎。

剩下的，我也就不用多說了吧…

4.2 同態加密的定義、安全性和簡單實例

下面的內容，如果可以接受符號表述，具有一點密碼學的知識，對抽象代數有一定的了解的話，可能體會的更深刻哦。

同態加密具體如何定義？

我們在雲計算應用場景下面進行介紹：

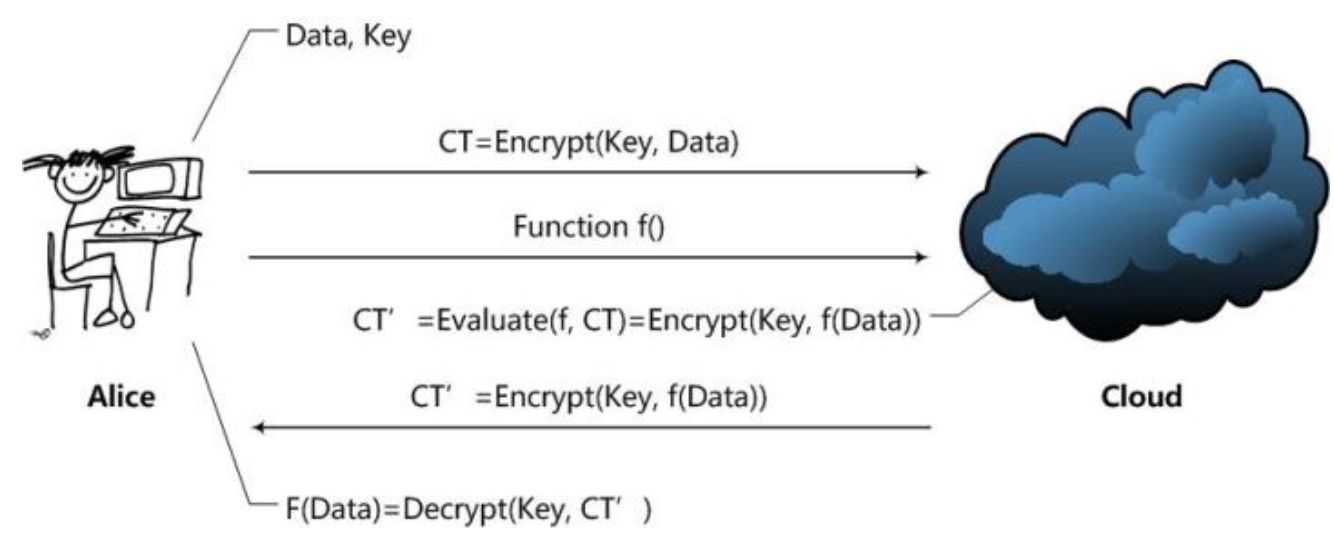
Alice通過Cloud，以Homomorphic Encryption（以下簡稱HE）處理數據的整個處理過程大致是這樣的：

Alice對數據進行加密。並把加密后的數據發送給Cloud；
Alice向Cloud提交數據的處理方法，這里用函數f來表示；
Cloud在函數f下對數據進行處理，並且將處理后的結果發送給Alice；
Alice對數據進行解密，得到結果。

據此，我們可以很直觀的得到一個HE方案應該擁有的函數：

KeyGen函數：密鑰生成函數。這個函數應該由Alice運行，用於產生加密數據Data所用的密鑰Key。當然了，應該還有一些公開常數PP（Public Parameter）；
Encrypt函數：加密函數。這個函數也應該由Alice運行，用Key對用戶數據Data進行加密，得到密文CT（Ciphertext）；
Evaluate函數：評估函數。這個函數由Cloud運行，在用戶給定的數據處理方法f下，對密文進行操作，使得結果相當於用戶用密鑰Key對f(Data)進行加密。
Decrypt函數：解密函數。這個函數由Alice運行，用於得到Cloud處理的結果f(Data)。

那么，f應該是什么樣子的呢？HE方案是支持任意的數據處理方法f？還是說只支持滿足一定條件的f呢？根據f的限制條件不同，HE方案實際上分為了兩類：

Fully Homomorphic Encryption (FHE)：這意味着HE方案支持任意給定的f函數，只要這個f函數可以通過算法描述，用計算機實現。顯然，FHE方案是一個非常棒的方案，但是計算開銷極大，暫時還無法在實際中使用。
Somewhat Homomorphic Encryption (SWHE)：這意味着HE方案只支持一些特定的f函數。SWHE方案稍弱，但也意味着開銷會變得較小，容易實現，現在已經可以在實際中使用。

什么叫做安全的HE？
HE方案的最基本安全性是語義安全性（Semantic Security）。直觀地說，就是密文（Ciphertext）不泄露明文（Plaintext）中的任意信息。這里密文的意思就是加密后的結果；明文的意思就是原始的數據。如果用公式表述的話，為：
$\forall m_0, m_1, \textbf{Encrypt}(PK, m_0) \approx \textbf{Encrypt}(PK, m_1)$
這里PK代表公鑰（Public Key），是非對稱加密體制中可以公開的一個量。公式中的"約等於"符號，意味着多項式不可區分性，即不存在高效的算法，可以區分兩個結果，即使已知m0, m1和PK。有人說了，這怎么可能？我已經知道m0, m1了，我看到加密結果后，對m0或者m1在執行一次加密算法，然后看哪個結果和給定結果相同不就完了？注意了，加密算法中還用到一個很重要的量：隨機數。也就是說，對於同樣的明文m進行加密，得到的結果都不一樣，即一個明文可以對應多個密文（many ciphertexts per plaintext）。

在密碼學中，還有更強的安全性定義，叫做選擇密文安全性（Chosen Ciphertext Security）。選擇密文安全性分為非適應性（None-Adaptively）和適應性（Adaptively），也就是CCA1和CCA2，HE方案是不可能做到CCA2安全的。那么，HE方案能不能做到CCA1安全呢？至今還沒有CCA1安全的FHE方案，但是在2010年，密碼學家們就已經構造出了CCA1的SWHE方案了[LMSV10]。

HE方案還有一方面的安全性，就是函數f是不是也可以保密呢？這樣的話HE就更厲害了！Cloud不僅不能夠得到數據本身的內容，現在連數據怎么處理的都不知道，只能按照給定的算法執行，然后返回的結果就是用戶想要的結果。如果HE方案滿足這樣的條件，我們稱這個HE方案具有Function-Privacy特性。不過，僅我個人所了解到的，現在還沒有Function-privacy FHE，甚至Function-privacy SWHE也沒有。

不過，Function-privacy引入了另一個很有趣的概念，那就是我們能不能反過來，就做到Function-privacy，但是不用做到數據隱私呢？這其實也有很好的應用場景：比如一個天才設計了一個算法（想象Jeffrey Dean設計了歷史上第一個O(1/n)復雜度算法，或者設計了一個O(n^2)算法，但是是用來解決旅行商問題的），但是他不想把這個算法公開。他只提供一個程序，這個程序不泄露任何算法本身的內容，人們只能調用這個算法，然后得到輸出的結果。這個特別像什么？對啦，就是程序的編譯與反編譯嘛。如果Function-privacy的加密設計出來了，那么計算機科學家們就可以一勞永逸地阻止程序反編譯，甚至連破解都杜絕了。滿足這樣條件的加密方案，即，給算法加密的方案，叫做Obfuscation。很遺憾，2001年，密碼學家們已經證明，不可能實現嚴格意義上的Obfuscation [BGIRSVY01]。但是，可以做到一個稱為Indistinguishability Obfuscation的東西。這個東西是密碼學家們研究同態加密過程中的一個產物，現在已經有了一些候選方案了[GGHRSB13]。這個就不展開說了，是另一個領域的內容。

舉個SWHE的例子？
在2009年Graig Gentry給出FHE的構造前，很多加密方案都具有Somewhat Homomorphism的性質。實際上，最最經典的RSA加密，其本身對於乘法運算就具有同態性。Elgamal加密方案同樣對乘法具有同態性。Paillier在1999年提出的加密方案也具有同態性，而且是可證明安全的加密方案哦！后面還有很多啦，比如Boneh-Goh-Nissim方案[BGN05], Ishai-Paskin方案等等。不過呢，2009年前的HE方案要不只具有加同態性，要不只具有乘同態性，但是不能同時具有加同態和乘同態。這種同態性用處就不大了，只能作為一個性質，這類方案的同態性一般也不會在實際中使用的。

在此我們看一下Elgamal加密方案，看看怎么個具有乘同態特性。Elgamal加密方案的密文形式為：
$CT=(C_1, C_2)=(gr,hr \cdot m)$
其中r是加密過程中選的一個隨機數，g是一個生成元，h是公鑰。如果我們有兩個密文：
$CT_1 = (g{r_1},h{r_1} \cdot m_1), CT_2 = (g{r_2},h{r_2} \cdot m_2)$
我們把這兩個密文的第一部分相乘，第二部分相乘，會得到：
$CT= (g^{r_1} \cdot g{r_2},h{r_1} \cdot m_1 \cdot h^{r_2} \cdot m_2)=(g^{r_1 + r_2}, h^{r_1 + r_2} \cdot m_1m_2)$
也就是說，相乘以后的密文正好是m1m2所對應的密文。這樣，用戶解密后得到的就是m1m2的結果了。而且注意，整個運算過程只涉及到密文和公鑰，運算過程不需要知道m1m2的確切值。所以我們說Elgamal具有乘同態性質。但是很遺憾，其沒有加同態性質。

HE的效率如何？
2011年，Gentry和Halevi在IBM嘗試實現了兩個HE方案：Smart-Vercauteren的SWHE方案[SV10]以及Gentry的FHE方案[Gen09]，並公布了效率。結果如何呢？我們給出Gentry公布的數據（原始數據可以在2nd Bar-Ilan Winter School on Cryptography找到）Smart-Vercauteren的SWHE方案效率如下：

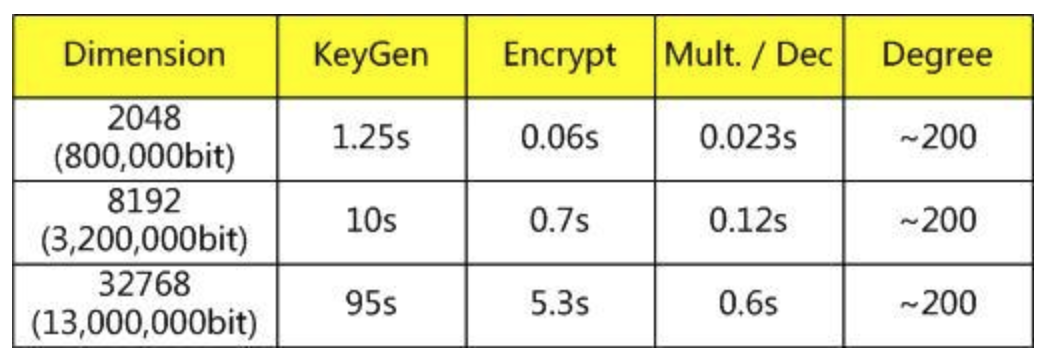
看着好像還行，不過這Dimension有點誇張啊…也就是說公鑰很長…那么，Gentry的FHE方案如何呢？效率如下：

公鑰2.3GB，KeyGen需要2個小時，也是醉了…

==============================

三、現有HE方案的安全假設和構造概覽

如果你致力於HE的研究，我們給出一些可用的資料。

如何證明HE方案的安全性？
對於現在的密碼學方案，安全性證明要把它規約到解決一個公開的困難問題上。簡單地說，就是如果方案被破解了，那么攻擊者可以用破解算法解決一個困難問題。然而，由於這個困難問題還沒有找到高效的（多項式復雜度的）算法，因此方案是安全的。

那么，2009年以后的HE方案是建立在哪個困難問題上呢？是一個被稱作Learning With Errors（LWE）的困難問題[Reg05]。后來，隨着另一個新的工具出現，密碼學家們又致力於基於Ring Learning With Errors（Ring-LWE）問題的HE構造[LPR10]。

Ring-LWE涉及到抽象代數中Ring以及Ideal的概念，稍顯復雜。我們這里簡單介紹一下LWE問題，Ring-LWE問題和它有點像。LWE問題分為兩類，一個叫做Search-LWE，一個叫做Decision-LWE。Search-LWE可以簡單地用下圖來表示，其中A是一個m*n的矩陣，由Zp中的元素組成；s是一個n維向量；e是一個m維向量；b是一個m維向量：

這個問題大致為：選擇一個秘密（secret）值s，並選擇一個范數很小的擾亂（error）向量e，計算b = As + e mod q。這個問題是：只給定矩陣A和計算的結果b（圖中紅色部分），不給定s和e（途中藍色部分），反過來求秘密值s的大小。Decision-LWE問題有點類似：給定A和b，算法需要判斷，b是由某個s通過As + e計算得來的呢，還是就是一個隨機量呢？這里有幾個小問題：

m和n有多大？這取決於我們要求安全度有多高了。實際上這還取決於一些其他因素。
e的范數要多么小？LWE要求e的取值要滿足離散高斯分布（Discrete Gaussian Distribution）。
怎么想到的這么個問題？實際上，LWE問題是Lattice中的一個問題。Lattice是什么呢？這個展開說就有點累了…

如果知乎er們想了解更多有關Abstract Algebra，Lattice，以及LWE的內容，下面的三個材料是可以閱讀的：

Harvard Extension School的Abstract Algebra課程。這門課可以幫助快速入門Abstract Algebra。當然了，這可是Harvard學生的本科課程哦。Abstract Algebra
2nd Bar-Ilan Winter School on Cryptography。Bar-llan大學自2011年開始每年都組織一次密碼學的Winter School，請的都是大牛啊！2012年的主題是Lattice-Based Cryptography，2013年的主題是Pairing-Based Cryptography。2015年2月，新的一輪Winter School就開始了，知乎上

@劉健

同學要去聽的哦，羡慕嫉妒恨呢！

2nd Bar-Ilan Winter School on Cryptography
Oded Regev的Lecture Notes on Lattice。Regev是誰？是他提出的LWE和Ring-LWE，所以他課程的材料當然有價值一聽。Lattices in Computer Science (Fall 2009)

介紹一下構造FHE的思路？

FHE最重要的一點是Fully，就是說要支持任意的函數f。因此我們也可以很明顯看出，想要構造FHE，就需要了解計算機是如何計算的。一般來說，我們有兩種思路：

從計算機原理考慮。計算機無論做何種運算，歸根到底都是位運算。那么，計算機至少要支持哪些位運算，才能夠支持所有的運算呢？實際上，一個計算機只要支持邏輯與運算（AND），以及異或運算（XOR），那么這個計算機理論上就可以實現計算機的其他運算了（我們稱之為圖靈完備性，Turing Completeness）
從抽象代數考慮。我們只需要加法和乘法就可以完成全部運算了。但其實更嚴格的說，只要我們在一個域（Field）上構造HE，理論上我們就可以支持所有的f。

基於LWE問題的FHE只能針對1 bit進行加密，因此現在的構造都是從計算機原理考慮。也就是在bit的層面上實現FHE方案，或者更嚴謹地說，從電路層（Circuit）實現FHE方案。具體構造呢，大家刻意參考下面給出的參考文獻了。實話實說，我自己也沒有都消化，或者更嚴格地說，Regev的LWE構造論文我還沒有完全看明白。

5. 零知識證明

零知識證明（ Zero-knowledge proofs）

鏈接：https://zhuanlan.zhihu.com/p/50121048

參考鏈接

零知識證明的提出

1985年 goid wasser, micali, rackoff 首次提出交互式零知識證明，發表了一篇名為《the knowledge complexity of interactive proof》的論文，他們的論文中首次提出了一個交互式證明系統，利用了圖靈機的計算模型，這個模型的特點是會預設一些接收或者拒絕的狀態，如果進入這些狀態，則停機，如果不能進入任何接收或者拒絕的狀態，則永不停機。也就是說，如果我們能輸入正確的信息，進入到圖靈機預設的狀態，那么圖靈機則會停機。

交互式證明系統定義：

定義 $L \subseteq{{0,1}^*}$ 這樣的一個正則語言，(P,V) 是圖靈機的一個交互對，V是一個多項式時間的，當滿足以下兩個條件時，則稱(P,V) 是關於L的一個交互式證明系統。

對 $\forall x \in L$ ,作為 (P,V) 的輸入，V接受並且停止的概率至少為 $1-\frac {1}{n^k}$ .
對任意的圖靈機 $P' , \forall x \notin L$ ,作為(P',V) 的輸入，V接受的最大概率是 $\frac{1}{n^k}$ .

其中，k表示次數，n表示輸入的長度。

什么意思呢，可以這樣理解，P和V在完成交互作用過程后，如果 $x\in L$ ,那么V在高概率的條件下相信這是事實，這一條成為完備性（completeness）,但如果 $x \notin L$ ，那么在高概率條件下P不可能欺騙V，使V相信 $x \in L$ ,這一條成為公正性（soundness）,有的也稱為正確性。這里提到的完備性和公正性就是零知識證明的性質的其中兩條，還有一條是零知識性（后面會再提到）。

為了使大家更好地理解這個概念，我們舉一個例子。

如圖，洞穴里有一個秘密，知道咒語的人能打開C和D之間的密門。對其他任何人來說，兩條通道都是死胡同。Peggy知道這個洞穴的秘密。她想對Victor證明這一點，但是她不想透露咒語。下面是她如何使Victor相信的過程：

Victor 站在A點。
Peggy一直走進洞穴，到達C點或者D點。
在Peggy消失在洞穴中之后，Victor走到B點。
Victor向Peggy喊叫，要她：
從左通道出來，或者從右通道出來。
Peggy答應了，如果有必要她就用咒語打開密門。
Peggy和Victor 重復第1~5步n次。

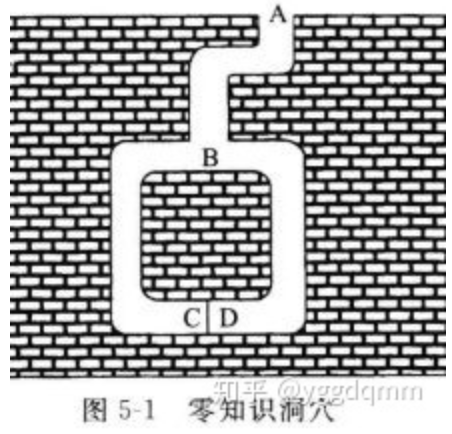
假設這個過程重復了十次，我們把這個例子放到剛才提到的交互式系統中，在Peggy知道咒語的情況下，那么她有很高的概率（ $1-\frac{1}{2^{10}}$ ）讓Victor相信她知道這個咒語（完備性），但是如果她不知道咒語，那么Victor相信的概率最大為 $\frac{1}{2^{10}}$ ,也就是有很高的概率Peggy沒法欺騙Victor（公正性）。

進一步設想一下，如果Victor和Peggy上面的交互過程用攝像機記錄下來，然后Victor拿給第三個人Carol看，Carol會相信嗎，答案是否定的，因為Peggy和Victor完全可以事先商量好進入哪個通道，從哪個通道出來，這樣Peggy在不知道咒語的情況下也可以正確的按照Victor的要求從通道走出來。或許他們不這么做，Peggy走進其中一條通道，Victor發出一個隨機的要求，如果Victor猜對了，好極了；如果他猜錯了，他們會從錄像帶中刪除這個試驗。總之，Victor獲得一個記錄，它准確顯示與實際證明Peggy知道咒語相同的事件順序。

這就說明了兩件事情，其一，Victor不可能使第三方相信這個證明的有效性；其二，它證明了這個協議是零知識的。在Peggy不知道咒語的情況下，Victor顯然不能從記錄中獲悉任何信息。但是，因為無法區分一個真實的記錄和一個偽造的記錄，所以Victor不能從實際證明中了解任何信息——它必定是零知識。

談到這里，大家應該多多少少對零知識證明有個大體的理解。下面給出零知識證明的形式化定義和零知識證明的性質以及基本的零知識協議。

零知識證明的形式化定義

零知識證明定義：知識的證明協議具有零知識性，是指存在一個多項式時間模擬器，能夠自行產生一些協議運行的腳本，該腳本與真實腳本有不可區分的概率分布。

怎么理解呢，還是用剛才的例子來說明，我們已經提及Victor沒辦法讓第三方Carol相信，原因就是Peggy和Victor可以模擬Peggy知道咒語的真實情況（存在一個多項式時間模擬器），但是這個真實情況和模擬的情況是沒辦法區分的（該腳本與真實腳本有不可區分的概率分布）。

零知識證明滿足的性質

(1)正確性。P無法欺騙V。換言之，若P不知道一個定理的證明方法，則P使V相信他會證明定理的概率很低。

(2)完備性。V無法欺騙P。若P知道一個定理的證明方法，則P使V以絕對優勢的概率相信他能證明。

在零知識協議中，除滿足上述兩個條件以外，還滿足下述的第三個性質。

(3)零知識性。V無法獲取任何額外的知識。

這三個性質，在前面的講解中已經解釋了，這里不再贅述。

基本的零知識協議

基本的交互式零知識證明協議的過程如下:

（1）證明者用所知道的信息和一個隨機數將這個難題轉變成另一難題，新的難題和原來的難題同構。然后用自己的信息和這個隨機數解這個新的難題。

（2）證明者利用位承諾方案提交這個新的難題的解法。

（3）證明者向驗證者透露這個新難題。驗證者不能用這個新難題得到關於原難題或其解法的任何信息。

（4）驗證者要求證明者:

(a)向他證明新、舊難題是同構的，或者:

(b)公開證明者在第（2）步中提交的解法並證明是新難題的解法。

（5）證明者同意。

（6）證明者和驗證者重復第（1）步至第（5）步 n 次。

非交互式零知識證明

我們在上文提到不能使Carol相信，因為這個協議是交互式的，並且Carol沒有介入交互中。為了讓Carol和其他感興趣的人相信，需要一個非交互式的協議。

基本的非交互零知識證明協議 過程如下：

（1）證明者使用他的信息和n 個隨機數把這個難題變換成n 個不同的同構難題，然后用他的信息和隨機數解決這n 個新難題。

（2）證明者提交這n 個新難題的解法。

（3）證明者把所有這些提交的解法作為一個單向散列函數的輸入，然后保存這個單向散列函數輸出的前n 個位。

（4）證明者取出在第 3 步中產生的n 個位，針對第i 個新難題依次取出這n個位中的第i 個位，並且：

(a)如果它是 0，則證明新舊問題是同構的，或者;

(b)如果它是 1，則公布他在第（2）步中提交的解法，並證明它是這個新問題的解法。

（5）證明者將第（2）步中的所有約定及第（4）步中的解法都公之於眾。

（6）驗證者或者其他感興趣的人，可以驗證第（1）步至第（5）步是否能被正確執行。

這個協議起作用的原因在於單向散列函數扮演一個無偏隨機位發生器的角色。如果證明者要進行欺騙，他必須能預測這個單向散列函數的輸出。但是，他沒有辦法強迫這個單向散列函數產生哪些位或猜中它將產生哪些位。這個單向散列函數在協議中實際上是驗證者的代替物—在第（4）步中隨機的選擇兩個證明中的一個。

零知識證明的應用

零知識證明是密碼學的一個高級協議，很多問題都有零知識證明的加密方案，但並不是所有問題都有，Goldreich,Micali和Wigderson給出了理論上存在零知識證明解的有效范圍。他們發現對於多項式時間內可以驗證解的決策問題（問題的答案僅為是/否）存在已知的零知識證明方案。

這里舉一個零知識證明的應用——哈密爾頓圖的交互式零知識證明和非交互式零知識證明。

哈密爾頓圖的交互式零知識證明

哈密爾頓圖（Hamiltonian Graph）是圖論中的一個重要概念。在一個圖中通過每一個頂點一次且僅一次的回路稱作哈密爾頓回路。有哈密爾頓回路的圖稱為哈密爾頓圖。現在尚不知道判斷一個圖是否是哈密爾頓圖的充要條件，即使知道判斷哈密爾頓圖的充要條件，要找到一個具體的哈密爾頓圖也是一個難題。

現在的問題是：有一個圖 G ，證明者知道這個圖的一個哈密爾頓回路。驗證者也知道這個圖，但不知道這個圖的哈密爾頓回路。現在證明者想要在不暴露哈密爾頓回路的條件下，向驗證者證明他知道這個圖的一個哈密爾頓回路。這個問題的解決方案是什么，零知識證明就派上用場了。

這里有一個事實是：如果證明者知道圖G 的一個哈密爾頓回路，那么他也能很容易找出這個圖的置換的哈密爾頓回路。

哈密爾頓圖的交互式零知識證明如下：

證明者隨機地生成圖的 G 一個置換H$，並加密H 到H' .
證明者將H' 的副本發送給驗證者。
驗證者要求證明者證明H' 是圖G 的同構副本的加密結果，或者出示H的哈密爾頓回路。
證明者通過解釋置換和解密證明H' 是圖G 的同構副本的加密結果，但不出示圖G ，H的哈密爾頓回路，或者只解密構成哈密爾頓回路的那些邊來出示$H$ 的哈密爾頓回路，但不證明圖G ,H 同構。
證明者和驗證者重復上述過程n次。

在一次協議中，證明者如果不知道圖G 的哈密爾頓回路，他最多能做的是創造一個圖H 與G 同構，或者創造一個與G 有相同點線的圖G' 及其哈密爾頓回路。也就是說，如果證明者不知道圖G的哈密爾頓回路，那么他就不可能每次都完成驗證者的要求。

完備性：假設證明者是誠實的協議參與者，嚴格按照協議的步驟執行協議，驗證者將以接近 1 的概率接受證明者的證明。

正確性：證明者如果不知道圖G的哈密爾頓回路，在每一輪協議中有 $\frac{1}{2}$ 的機會欺騙驗證者，協議執行n 次以后，證明者欺騙驗證者成功的概率為 $\frac{1}{2^n}$ ,驗證者以 $1-\frac{1}{2^n}$ 的概率拒絕證明者的證明。