2019/3/25
一元線性回歸——梯度下降/最小二乘法又名:一兩位小數點的悲劇
感覺這個才是真正的重頭戲,畢竟前兩者都是更傾向於直接使用公式,而不是讓計算機一步步去接近真相,而這個梯度下降就不一樣了,計算機雖然還是跟從現有語句/公式,但是在不斷嘗試中一步步接近目的地。
簡單來說,梯度下降的目的在我看來還是要到達兩系數的偏導數函數值為零的取值,因此,我們會從“任意一點”開始不斷接近,由於根據之前最小二乘法的推導,可以說方差的公式應該算一個二次函數...?總之,這么理解的話就算只用中學知識也能知道在導數值為0時求得最大/小值。
那么就很簡單了,我們讓a,b一點點接近就可以了,而逼近的過程十分有趣,且巧妙。當前點的導數值如果為正,說明該點的橫坐標需要左移,而為負則需要右移(為0就勝利了),因此根據這個特性我們可以直接設定為以下python代碼:
a=a-n*get_pa(c,d)
b=b-n*get_pb(c,d)
其中,get_pa()以及get_pb()對應的分別為a或b求偏導數值,以a,b兩個值為輸入值,而n則是非常重要的調節系數,重要到讓我無法正常運行程序,后文會着重提及。
運用到了正減,負增,通過減法實現,很巧妙【來自於Coursera的華盛頓大學“機器學習:回歸”課程的想法
接下來,還是先給出求方差,求偏導的函數。
求方差:
def get_sqm(a,b):
sqm=0
for i in range(100):
sqm=sqm+(cols2[i]-a-b*cols1[i])*(cols2[i]-a-b*cols1[i])
return sqm
求a,b的偏導:
def get_pa(a,b):
pa=0
for i in range(100):
pa=pa-2*(cols2[i]-a-b*cols1[i])
return pa
def get_pb(a,b):
pb=0
for i in range(100):
pb=pb-2*cols1[i]*(cols2[i]-a-b*cols1[i])
return pb
好像...也沒有太多可說的?那就迫不及待的進入正題吧!來自於我被調節系數n折磨的一整個下午的怨念!其實主題的循環函數並不是那么難理解和構建,我很早就完成了:
while abs(get_pa(a,b))>=10 and abs(get_pb(a,b))>=10 :
c=a
d=b
a=a-n*get_pa(c,d)
b=b-n*get_pb(c,d)
print(get_sqm(a,b))
偏導數的限制...我取了10...看起來很驚悚,但也是沒辦法,被嚇得,只能松一點了。
簡單來說就是不斷調整兩個系數取值,而且最終要的,也是我用臨時變量c,d的原因,a,b要同時調整,或者說,在當前情況下,由於兩偏導數都是既有a又有b的,牽一發而動全身,調完一個另一個也有了變化,不再准確,也不是之前的那個對應點的偏導數值了。
同時,n的存在也非常重要,它是外部限制調節幅度的方式,而它的取值又非常玄學,沒有一個定論......對於不同的數據有不同的措施,在Coursera上建議的0.1把我坑慘了。
使用0.1,最后只會給我兩個藍藍的“nan”,大概是python中的某一個錯誤表達吧,反正我一直以為我代碼有問題,直到晚上才隨手靈機一動,加了幾個0,然后——就成功了...
【太過於戲劇性了,我的焦慮完全一筆帶過
在同時我也打印出當前的方差,若是n取0.0001,則顯示出的數據為大約又450多行,象征性的表示一下
59842.51109094548
44733.39899894902
...
27787.81855782964
27787.002777912836
能感受到前后變化的差距,最后的a,b值也不錯,差別不大【偏導數限制在10好像也沒什么大關系...
-
最小二乘法公式法
a=-22.63450339669057 b=13.449314363947979 -
梯度下降(n=0.0001,偏導數約束為10)
a=-21.128787257903344 b=13.281329019963474 -
梯度下降(n=0.0001,偏導數約束為1)
a=-22.48409512730926 b=13.432534053091723 -
梯度下降(n=0.00001,偏導數約束為1)
a=-22.483484868708103 b=13.432465969541052
目前來看,下降偏導數約束帶來的提升可能比調整系數的下降來的多?不過畢竟直接從10減到了1,幅度比n的變化不知道大了多少。
n=0.0001,少一個0,就會有倆“nan”看着我,氣
由於圖像上的差異並不大所以就用n=0.00001,偏導數約束為1的圖像吧,不能讓它白跑那么久:
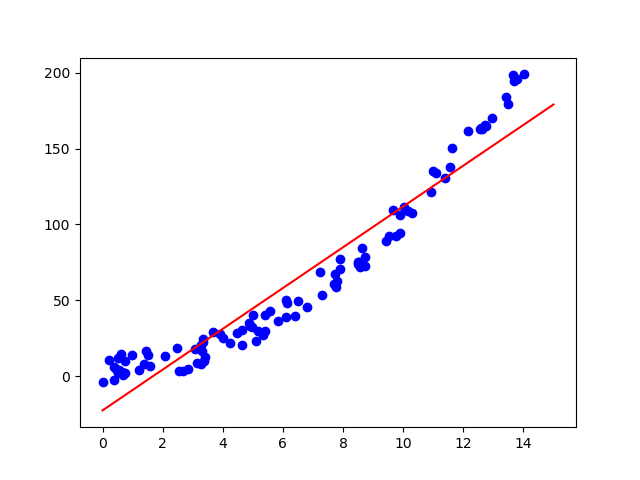
用的還是這個更像二次的數據,湊合看吧。
這里給出完整代碼:
import xlrd
import xlwt
import sympy as sp
import matplotlib.pyplot as plt
import numpy as np
workbook=xlrd.open_workbook(r'1.xls')
sheet=workbook.sheet_by_index(0)
cols1=sheet.col_values(0) #獲取第一列
cols2=sheet.col_values(1) #獲取第二列
#a+bx
#a=sp.Symbol('a')
#b=sp.Symbol('b')
#已知a=-22.63450339669057 b=13.449314363947979
def get_sqm(a,b):
sqm=0
for i in range(100):
sqm=sqm+(cols2[i]-a-b*cols1[i])*(cols2[i]-a-b*cols1[i])
return sqm
def get_pa(a,b):
pa=0
for i in range(100):
pa=pa-2*(cols2[i]-a-b*cols1[i])
return pa
def get_pb(a,b):
pb=0
for i in range(100):
pb=pb-2*cols1[i]*(cols2[i]-a-b*cols1[i])
return pb
n=0.00001
a=0.0
b=0.0
while abs(get_pa(a,b))>=1 and abs(get_pb(a,b))>=1 :
c=a
d=b
a=a-n*get_pa(c,d)
b=b-n*get_pb(c,d)
print(get_sqm(a,b))
print(a,b)
plt.scatter(cols1,cols2,color = 'blue')
x=np.linspace(0,15,100)
y=b*x+a
plt.plot(x,y,color="red")
plt.show()
就先這樣,草草結束了先...?
