DTW(動態時間調整)

動態時間調整算法是大多用於檢測兩條語音的相似程度,由於每次發言,每個字母發音的長短不同,會導致兩條語音不會完全的吻合,動態時間調整算法,會對語音進行拉伸或者壓縮,使得它們竟可能的對齊。
如上圖紅圈標注的位置,可以發現下面那條線中有許多的點與之對應,如果換成一個個離散的點表示的話,實際上是對上一條曲線該點進行了拉伸處理,使得它們最大化對齊。
最近在研究時間序列的問題,時間序列類似這個。假如我想計算兩條天氣的時間序列是否相似,由於時間序列有的時候會出現延遲的現象,導致兩條時間序列吻合的不好,可以通過這樣的方法來准確的計算。
這個算法的實現和動態規划十分相似。
為了對齊這兩個序列,我們需要構造一個n x m的矩陣網格,矩陣元素(i, j)表示qi和cj兩個點的距離d(qi, cj)(也就是序列Q的每一個點和C的每一個點之間的相似度,距離越小則相似度越高。這里先不管順序),一般采用歐式距離,d(qi, cj)= (qi-cj)2(也可以理解為失真度)。每一個矩陣元素(i, j)表示點qi和cj的對齊。DP算法可以歸結為尋找一條通過此網格中若干格點的路徑,路徑通過的格點即為兩個序列進行計算的對齊的點。

那么這條路徑我們怎么找到呢?那條路徑才是最好的呢?也就是剛才那個問題,怎么樣的warping才是最好的。
注明:兩個序列長度不同,不能使用歐氏距離進行匹配。使用dtw時,上圖方格中的每個連續的點(開頭(1,1)和結尾(m,n)還是要保證的)構成的曲線都有可能,這是就要找出代價最小的那條曲線,如圖中標出的黑色曲線。
我們把這條路徑定義為warping path規整路徑,並用W來表示, W的第k個元素定義為wk=(i,j)k,定義了序列Q和C的映射。這樣我們有:

首先,這條路徑不是隨意選擇的,需要滿足以下幾個約束:
1)邊界條件:w1=(1, 1)和wK=(m, n)。任何一種語音的發音快慢都有可能變化,但是其各部分的先后次序不可能改變,因此所選的路徑必定是從左下角出發,在右上角結束。
2)連續性:如果wk-1= (a’, b’),那么對於路徑的下一個點wk=(a, b)需要滿足 (a-a’) <=1和 (b-b’) <=1。也就是不可能跨過某個點去匹配,只能和自己相鄰的點對齊。這樣可以保證Q和C中的每個坐標都在W中出現。
3)單調性:如果wk-1= (a’, b’),那么對於路徑的下一個點wk=(a, b)需要滿足0<=(a-a’)和0<= (b-b’)。這限制W上面的點必須是隨着時間單調進行的。以保證圖B中的虛線不會相交。
結合連續性和單調性約束,每一個格點的路徑就只有三個方向了。例如如果路徑已經通過了格點(i, j),那么下一個通過的格點只可能是下列三種情況之一:(i+1, j),(i, j+1)或者(i+1, j+1)。

滿足上面這些約束條件的路徑可以有指數個,然后我們感興趣的是使得下面的規整代價最小的路徑:

分母中的K主要是用來對不同的長度的規整路徑做補償。我們的目的是什么?或者說DTW的思想是什么?是把兩個時間序列進行延伸和縮短,來得到兩個時間序列性距離最短也就是最相似的那一個warping,這個最短的距離也就是這兩個時間序列的最后的距離度量。在這里,我們要做的就是選擇一個路徑,使得最后得到的總的距離最小。
這里我們定義一個累加距離cumulative distances。從(0, 0)點開始匹配這兩個序列Q和C,每到一個點,之前所有的點計算的距離都會累加。到達終點(n, m)后,這個累積距離就是我們上面說的最后的總的距離,也就是序列Q和C的相似度。
累積距離γ(i,j)可以按下面的方式表示,累積距離γ(i,j)為當前格點距離d(i,j),也就是點qi和cj的歐式距離(相似性)與可以到達該點的最小的鄰近元素的累積距離之和:

注明:先把模板序列和測試序列的每個點相對應的距離算出來,構成一個m xn的矩陣。然后根據每個元素的代價計算一條最短路徑。這里的計算要符合以上三個約束。即,一個點的代價=這個點的值+來自min{下、左、斜下這三個方向的值}。下、左、斜下這三個方向的值可以依次遞歸求得,直到(1,1)點
3 例子
這個例子中假設標准模板R為字母ABCDEF(6個),測試模板T為1234(4個)。R和T中各元素之間的距離已經給出。如下:

既然是模板匹配,所以各分量的先后匹配順序已經確定了,雖然不是一一對應的。現在題目的目的是要計算出測試模板T和標准模板R之間的距離。因為2個模板的 長度不同,所以其對應匹配的關系有很多種,我們需要找出其中距離最短的那條匹配路徑。現假設題目滿足如下的約束:當從一個方格((i-1,j-1)或者 (i-1,j)或者(i,j-1))中到下一個方格(i,j),如果是橫着或者豎着的話其距離為d(i,j),如果是斜着對角線過來的則是 2d(i,j).其約束條件如下圖像所示:

其中g(i,j)表示2個模板都從起始分量逐次匹配,已經到了M中的i分量和T中的j分量,並且匹配到此步是2個模板之間的距離。並且都是在前一次匹配的結果上加d(i,j)或者2d(i,j),然后取最小值。
所以我們將所有的匹配步驟標注后如下:

怎么得來的呢?比如說g(1,1)=4, 當然前提都假設是g(0,0)=0,就是說g(1,1)=g(0,0)+2d(1,1)=0+2*2=4.
g(2,2)=9是一樣的道理。首先如果從g(1,2)來算的話是g(2,2)=g(1,2)+d(2,2)=5+4=9,因為是豎着上去的。
如果從g(2,1)來算的話是g(2,2)=g(2,1)+d(2,2)=7+4=11,因為是橫着往右走的。
如果從g(1,1)來算的話,g(2,2)=g(1,1)+2*d(2,2)=4+2*4=12.因為是斜着過去的。
綜上所述,取最小值為9. 所有g(2,2)=9.
當然在這之前要計算出g(1,1),g(2,1),g(1,2).因此計算g(I,j)也是有一定順序的。
其基本順序可以體現在如下:

計算了第一排,其中每一個紅色的箭頭表示最小值來源的那個方向。當計算了第二排后的結果如下:

最后都算完了的結果如下:

到此為止,我們已經得到了答案,即2個模板直接的距離為26. 我們還可以通過回溯找到最短距離的路徑,通過箭頭方向反推回去。如下所示:


注明:不管哪個方向,我都只加上了其本身的數值,即d(i j),沒有x2.得出的路徑是一樣的。
PYTHON代碼一個簡單的例子
import numpy as np # We define two sequences x, y as numpy array # where y is actually a sub-sequence from x x = np.array([2, 0, 1, 1, 2, 4, 2, 1, 2, 0]).reshape(-1, 1) y = np.array([1, 1, 2, 4, 2, 1, 2, 0]).reshape(-1, 1) from dtw import dtw euclidean_norm = lambda x, y: np.abs(x - y) d, cost_matrix, acc_cost_matrix, path = dtw(x, y, dist=euclidean_norm) print(d) >>> 0.1111111111111111 # Only the cost for the insertions is kept # You can also visualise the accumulated cost and the shortest path import matplotlib.pyplot as plt plt.imshow(acc_cost_matrix.T, origin='lower', cmap='gray', interpolation='nearest') plt.plot(path[0], path[1], 'w') plt.show()
結果圖中的白線,就是尋找到的兩條曲線的最小距離,曲線的開始是直線,縱坐標的零點對應橫坐標的0,和2點,說明對該處進行了拉伸。
DTW Barycenter Averaging (DBA)
DBA 是在DTW的基礎上做重心平均,為什么這么做,因為往往我們需要比較的時間序列不是一條而是一個集合,所以通過把時間序列壓縮成一條來進行比較
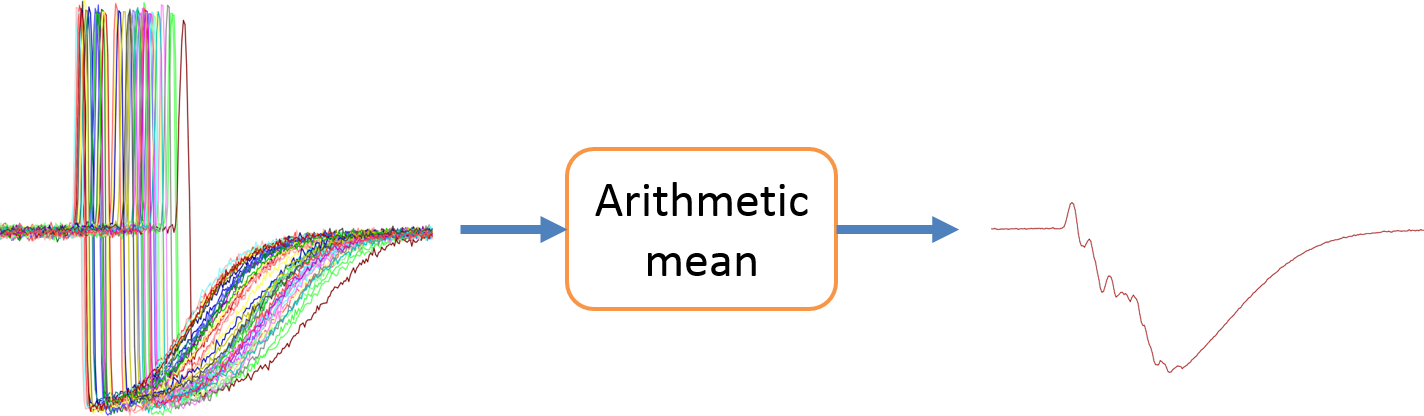
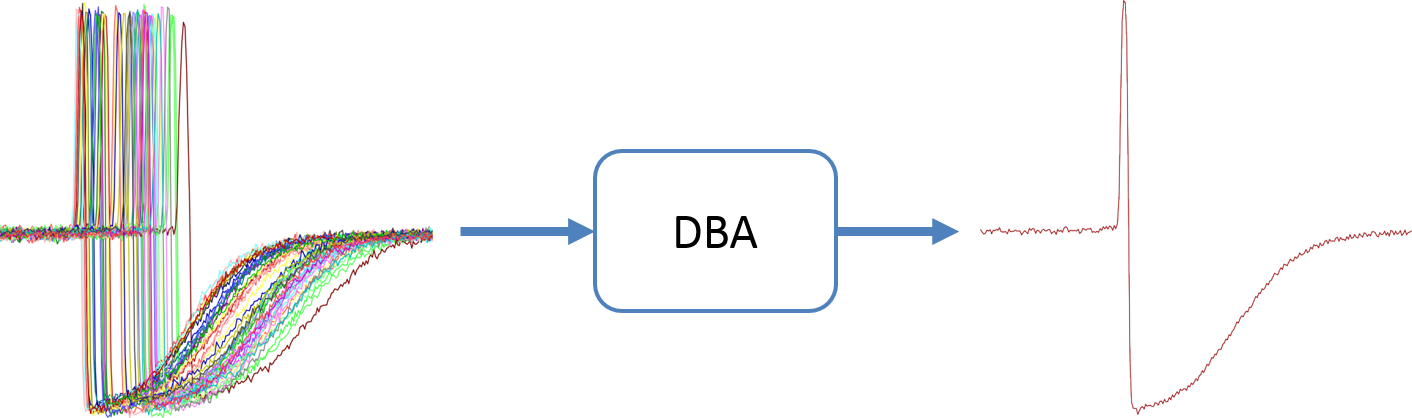
DBA代表動態時間扭曲重心平均。DBA是一種與動態時間扭曲一致的平均方法。下面給出一個時間序列集合的傳統算術平均值與DBA之間的區別的例子。
上圖可知,DBA的結果要好於傳統的求平均值結果。接下來介紹DBA算法,這個過程是一個迭代過程,每一次迭代都會執行以下兩步。
(1) 計算每個單獨時間序列與待細化的臨時平均序列之間的DTW,為了找出平均序列的坐標與時間序列集合的坐標之間的關系(其實就是找相似性)。
(2)在第一步中,將平均序列的每個坐標更新為與之關聯的重心坐標。
Let S = {S1, · · · , SN} 為要取平均值的時間序列集,
let C = (C1, . . . , CT )為迭代第 i 次和的平均序列
let C' = (C1'.......,CT') 為迭代i+1次對C集合的更新
我們要找到它的坐標。此外,平均序列的每個坐標都定義在任意向量空間E中(通常使用歐幾里得距離)

我們假設一個函數assoc,它將平均序列的每個坐標與S序列的一個或多個坐標聯系起來。這個函數是在計算C和S序列之間的DTW時計算出來的。然后定義 t 次平均序列 Ct' 的坐標為

Where

然后,通過再次計算平均序列與所有S序列之間的DTW,可以改變DTW產生的關聯。由於無法預測這些關聯將如何變化,我們建議讓C迭代收斂。下圖顯示了四個迭代(即(四次更新),其中一個例子包含兩個序列。


綜上所述,本文提出的動態時間扭曲平均方法是一種全局方法,可以對一組序列進行平均。兩個迭代之間的平均序列的更新與各個序列用於計算它們對所述更新的貢獻的順序無關。圖3顯示了一個使用DBA在[19]的一個數據集上計算平均序列的示例。這個圖顯示DBA保留了DTW的能力,可以識別時間的變化。

- Pattern Recognition 2011: A global averaging method for Dynamic Time Warping
Transfer learning for time series classification
這篇論文是講把遷移學習的思想用到時間序列的訓練上,最新穎的地方是使用DTW來比較兩個時間序列的相似性。
如果遇到時間序列集,使用DAB來整合一個時間序列集為一條時間序列,再使用DTW來比較相識性。
選用到訓練模型是一般的CNN(卷積神經網絡),遷移的方法是,對於不同時間序列集通過修改最后一層的 softmax 實現遷移。
使用熱力圖來表示不同的數據集使用遷移學習的效果,有的不僅沒有提高反而惡化,有的和沒有使用遷移學習一樣,有的有所提高。
說明了遷移學習對於相似的時間序列訓練具有優勢。
但是我覺得把遷移學習用於時間序列還是十分局限,條件也很多,兩條時間序列相似的時候才會獲得較好的效果,否則適得其反,會更加糟糕。
對於圖片的遷移學習比較順利,因為圖片在抽象層中具有相似性,比較普遍,統一類圖像就可以用遷移學習能獲得很好的效果,而且已經存在訓練好的模型VGG16,用於遷移學習十分方便,所以能不能訓練一個通用的時間序列模型?