# 實驗題部分
## 基本題
### 1、簡述sketch: - 對於數據流中大量的元素要統計其特征(出現頻率,數據流大小),對數據流多次使用哈希函數將事件映射到頻率,在合理的偏差內估計其大小,並顯著減少內存占用,是一種可靠性較高的概率統計數據結構。
### 2、Count-min Sketch: - 預備知識1:通過把關鍵碼值映射到表中一個位置來訪問記錄,以加快查找的速度,這個映射函數叫做哈希函數或散列函數。主要操作是對數據進行加法、乘法和移位運算。 - 預備知識2:Hash函數的基本特性: - 1.經過hash后能夠得到相應輸入的散列值。如果兩個散列值是不相同的(根據同一函數),那么這兩個散列值的原始輸入也是不相同的; - 2.散列函數的輸入和輸出不是一一對應的,如果兩個散列值相同,兩個輸入值很可能是相同的但不絕對肯定一定相等(可能出現哈希碰撞)。 - 算法過程: > 使用d個hash函數,每個hash函數的取值范圍都在[1,w]內,從而可以組成一個d * w的二維數組(hash table),該二維數組的長度大小固定。對於每個二元組(k, v),代表元素k需要更新v次,則分別使用d個hash函數對k進行hash操作,得到d個mapped counters,然后對它們全部增加v(即需要更新的數據)。***(count含義)*** 當需要查詢某個元素的頻率估計值時,也是先根據hash函數得到mapped counters,然后取其中的最小值即可,因為最小代表了沖突次數最少,相對最精確。***(min含義)***
-- 摘引自他人博客《Sketch調研[https://blog.csdn.net/u012332103/article/details/79702495]》,有刪改 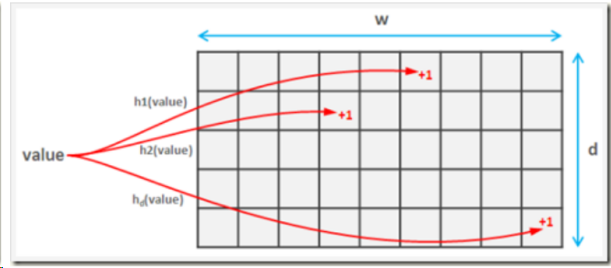
# 開放題部分
## 理論部分
### 1、解釋為什么 sketch 可以省空間 Count-min-sketch在處理數據時引入了hash函數,能夠把一個大范圍映射到一個固定大小的小范圍(簡單來說,就是將任意長度的二進制值映射為固定長度的、大小唯一的較小二進制值),往往是為了節省空間、加快存取,使得數據容易保存。該函數是CM-Sketch能夠極大節省空間的一個關鍵。 但是相應的代價是:由於上述hash函數的特性,多個key的散列值可能相同(哈希碰撞),從而導致探測計數器的估計值偏大。 因此為了減少哈希碰撞的概率: - 1、可使用多個哈希函數; - 2、可使用一個相對於數據足夠大的素數進行hash操作;(例如2的32次方附近) - 3、提高d和w的大小(越大精度越高),但是相應的在估計中使用空間也會增大。
### 2、用流程圖描述Count-min sketch的算法過程

備注:
- 1、Ai->Bi,就是IP和對應的請求大小;
- 2、update(Ai, Bi)包括了接下來的hash操作,是給Ai的原對應值上再添加Bi的值;
- 3、estimate(Ai),得到各個探測計數器中的最小值並返回最小值;
- 4、邊輸入邊算,這種流程圖的方法,可能會多次重復輸出已經輸出過的Ai->Bi。
### 3、拿它和你改進后方法進行對比,分析優劣
優點:
- 1、只需利用相對獨立的hash函數就能夠解決內存占用問題,對龐大的數據流可以實時處理,直接通過hash函數也可以直接找到的對應的value,無需遍歷,降低時間空間復雜度。
- 2、不需要精確估計數據包大小,適用於范圍性問題,雖然結果可能偏大,但是理論上可以控制在合理誤差范圍內。
- 3、拓展性強,由於不容易受數據長度大小的影響,加上鍵-值對應,在此基礎上可以發展成統計其他數據特征的數據結構。本人的原始代碼只能處理一種定長格式的數據的其中一種特征。
劣勢:
- 1、CM-Sketch的實現難度明顯高於本人的代碼,需要更深的知識掌握(例如兩兩獨立的hash函數要如何創建),如果要求更高的精度,代碼將會越復雜。
- 2、對於低頻的數據估計值誤差會偏大,可能不適用於需要太過精確判斷的問題中。
### 4、吐槽Count-min sketch
- 1、外國人寫個代碼還好基本對函數和基本單元進行了封裝,不然真的看不懂;
- 2、低頻數據的准確度有時差到驚人,甚至有內存分配出錯的狀態發生(或許是我改動完以后的問題)(二更:不是我的問題, 代碼自身的hash算法其中的大數運算導致的,已修改);
- 3、hash算法和整體架構修改起來並不簡單,但是看懂之后才會好很多。而且貌似偶爾會導致堆損壞?這個問題很不解,但是免不了對堆的維護,但它不會中斷程序(如下截圖,其中一次堆損壞)。

