卷積神經網絡CNN全面解析

• 卷積神經網絡（CNN）概述
• 從多層感知器（MLP）說起
  • 感知器
  • 多層感知器
    • 輸入層-隱層
    • 隱層-輸出層
  • Back Propagation
  • 存在的問題
• 從MLP到CNN
  • CNN的前世今生
  • CNN的預測過程
    • 卷積
    • 下采樣
    • 光柵化
    • 多層感知器預測
  • CNN的參數估計
    • 多層感知器層
    • 光柵化層
    • 池化層
    • 卷積層
• 最后一公里：Softmax
• CNN的實現
  • 思路
  • 其他

---

最近仔細學習了一下卷積神經網絡（CNN，Convolutional Neural Network），發現各處資料都不是很全面，經過艱苦努力終於弄清楚了。為了以后備查，以及傳播知識，決定記錄下來。本文將極力避免廢話，重點聚焦在推導過程上，為打算從零開始的孩紙說清楚“為什么”。

另外，因本人才疏學淺（是真的才疏學淺，不是謙虛），肯定會有很多謬誤，歡迎大家指出！

卷積神經網絡（CNN）概述

• 由來：神經元網絡的直接升級版
• 相關：Yann LeCun和他的LeNet
• 影響：在圖像、語音領域不斷突破，復興了神經元網絡並進入“深度學習”時代

卷積神經網絡沿用了普通的神經元網絡即多層感知器的結構，是一個前饋網絡。以應用於圖像領域的CNN為例，大體結構如圖1。

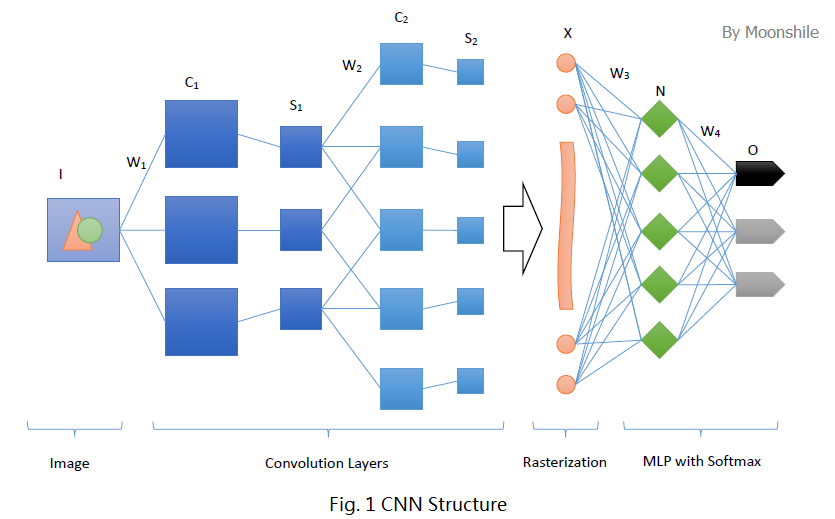
很明顯，這個典型的結構分為四個大層次

• 輸入圖像I。為了減小復雜度，一般使用灰度圖像。當然，也可以使用RGB彩色圖像，此時輸入圖像有三張，分別為RGB分量。輸入圖像一般需要歸一化，如果使用sigmoid激活函數，則歸一化到[0, 1]，如果使用tanh激活函數，則歸一化到[-1, 1]。
• 多個卷積（C）-下采樣（S）層。將上一層的輸出與本層權重W做卷積得到各個C層，然后下采樣得到各個S層。怎么做以及為什么，下面會具體分析。這些層的輸出稱為Feature Map。
• 光柵化（X）。是為了與傳統的多層感知器全連接。即將上一層的所有Feature Map的每個像素依次展開，排成一列。
• 傳統的多層感知器（N&O）。最后的分類器一般使用Softmax，如果是二分類，當然也可以使用LR。

接下來，就開始深入探索這個結構吧！

從多層感知器（MLP）說起

卷積神經網絡來源於普通的神經元網絡。要了解個中淵源，就要先了解神經元網絡的機制以及缺點。典型的神經元網絡就是多層感知器。

摘要：本節主要內容為多層感知器（MLP，Multi-Layer Perceptron）的原理、權重更新公式的推導。熟悉這一部分的童鞋可以直接跳過了~但是，一定一定要注意，本節難度比較大，所以不熟悉的童鞋一定一定要認真看看！如果對推導過程沒興趣，可直接在本節最后看結論。

感知器

感知器（Perceptron）是建立模型

 

f(x)=act(θTx+b)f(x)=act(θTx+b)

 

其中激活函數 act 可以使用{sign, sigmoid, tanh}之一。

• 激活函數使用符號函數 sign ，可求解損失函數最小化問題，通過梯度下降確定參數
• 激活函數使用 sigmoid （或者 tanh ），則分類器事實上成為Logistic Regression（個人理解，請指正），可通過梯度上升極大化似然函數，或者梯度下降極小化損失函數，來確定參數
• 如果需要多分類，則事實上成為Softmax Regression
• 如要需要分離超平面恰好位於正例和負例的正中央，則成為支持向量機（SVM）。

感知器比較簡單，資料也比較多，就不再詳述。

多層感知器

感知器存在的問題是，對線性可分數據工作良好，如果設定迭代次數上限，則也能一定程度上處理近似線性可分數據。但是對於非線性可分的數據，比如最簡單的異或問題，感知器就無能為力了。這時候就需要引入多層感知器這個大殺器。

多層感知器的思路是，盡管原始數據是非線性可分的，但是可以通過某種方法將其映射到一個線性可分的高維空間中，從而使用線性分類器完成分類。圖1中，從X到O這幾層，正展示了多層感知器的一個典型結構，即輸入層-隱層-輸出層。

輸入層-隱層

是一個全連接的網絡，即每個輸入節點都連接到所有的隱層節點上。更詳細地說，可以把輸入層視為一個向量 xx ，而隱層節點 jj 有一個權值向量 θjθj 以及偏置 bjbj ，激活函數使用 sigmoid 或 tanh ，那么這個隱層節點的輸出應該是

 

fj(x)=act(θTjx+bj)fj(x)=act(θjTx+bj)

 

也就是每個隱層節點都相當於一個感知器。每個隱層節點產生一個輸出，那么隱層所有節點的輸出就成為一個向量，即

 

f(x)=act(Θx+b)f(x)=act(Θx+b)

 

若輸入層有 mm 個節點，隱層有 nn 個節點，那么 Θ=[θT]Θ=[θT] 為 n×mn×m 的矩陣，xx 為長為 mm 的向量，bb 為長為 nn 的向量，激活函數作用在向量的每個分量上， f(x)f(x) 返回一個向量。

隱層-輸出層

可以視為級聯在隱層上的一個感知器。若為二分類，則常用Logistic Regression；若為多分類，則常用Softmax Regression。

Back Propagation

搞清楚了模型的結構，接下來就需要通過某種方法來估計參數了。對於一般的問題，可以通過求解損失函數極小化問題來進行參數估計。但是對於多層感知器中的隱層，因為無法直接得到其輸出值，當然不能夠直接使用到其損失了。這時，就需要將損失從頂層反向傳播（Back Propagate）到隱層，來完成參數估計的目標。

首先，約定標量為普通小寫字母，向量為加粗小寫字母，矩陣為加粗大寫字母；再約定以下記號：

• 輸入樣本為 xx，其標簽為 tt
• 對某個層 QQ ，其輸出為 oQoQ ，其第 jj 個節點的輸出為 o(j)QoQ(j) ，其每個節點的輸入均為上一層 PP 的輸出 oPoP ；層 QQ 的權重為矩陣 ΘQΘQ ，連接層 PP 的第 ii 個節點與層 QQ 的第 jj 個節點的權重為 θ(ji)QθQ(ji)
• 對輸出層 YY ，設其輸出為 oYoY， 其第 yy 個節點的輸出為 o(y)YoY(y)

現在可以定義損失函數

 

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪Eo(j)Qn(j)Q=12∑y∈Y(t(y)−o(y)Y)2=ϕ(n(j)Q)=∑i∈Pθ(ji)Qo(i)P+b(j)Q{E=12∑y∈Y(t(y)−oY(y))2oQ(j)=ϕ(nQ(j))nQ(j)=∑i∈PθQ(ji)oP(i)+bQ(j)

 

其中， ϕϕ 為激活函數。我們依舊通過極小化損失函數的方法，嘗試進行推導。則

 

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪∂E∂θ(ji)Q∂E∂b(j)Q=∂E∂o(j)Q∂o(j)Q∂n(j)Q∂n(j)Q∂θ(ji)Q=∂E∂o(j)Q∂o(j)Q∂n(j)Q∂n(j)Q∂b(j)Q{∂E∂θQ(ji)=∂E∂oQ(j)∂oQ(j)∂nQ(j)∂nQ(j)∂θQ(ji)∂E∂bQ(j)=∂E∂oQ(j)∂oQ(j)∂nQ(j)∂nQ(j)∂bQ(j)

 

上邊兩個式子的等號右邊部有三個導數比較容易確定

 

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪∂o(j)Q∂n(j)Q∂n(j)Q∂θ(ji)Q∂n(j)Q∂b(j)Q=ϕ′(n(j)Q)=o(i)P=1{∂oQ(j)∂nQ(j)=ϕ′(nQ(j))∂nQ(j)∂θQ(ji)=oP(i)∂nQ(j)∂bQ(j)=1

 

然后再看剩下的比較復雜的一個偏導數。考慮層 QQ 的下一層 RR ，其節點 kk 的輸入為層 QQ 中每個節點的輸出，也就是為 o(j)QoQ(j) 的函數，考慮逆函數，可視 o(j)QoQ(j) 為 o(k)RoR(k) 的函數，也為 n(k)RnR(k) 的函數。則對每個隱層

 

∂E∂o(j)Q=∂E(n(1)R,n(2)R,...,n(k)R,...,n(K)R)∂o(j)Q=∑k∈R∂E∂n(k)R∂n(k)R∂o(j)Q=∑k∈R∂E∂o(k)R∂o(k)R∂n(k)R∂n(k)R∂o(j)Q=∑k∈R∂E∂o(k)R∂o(k)R∂n(k)Rθ(kj)R∂E∂oQ(j)=∂E(nR(1),nR(2),...,nR(k),...,nR(K))∂oQ(j)=∑k∈R∂E∂nR(k)∂nR(k)∂oQ(j)=∑k∈R∂E∂oR(k)∂oR(k)∂nR(k)∂nR(k)∂oQ(j)=∑k∈R∂E∂oR(k)∂oR(k)∂nR(k)θR(kj)

 

令 δ(j)Q=∂E∂o(j)Q∂o(j)Q∂n(j)QδQ(j)=∂E∂oQ(j)∂oQ(j)∂nQ(j)

則對每個隱層

 

∂E∂o(j)Q=∑k∈R∂E∂o(k)R∂o(k)R∂n(k)Rθ(kj)R=∑k∈Rδ(k)Rθ(kj)R∂E∂oQ(j)=∑k∈R∂E∂oR(k)∂oR(k)∂nR(k)θR(kj)=∑k∈RδR(k)θR(kj)

 

考慮到輸出層，有

 

∂E∂o(j)Q=⎧⎩⎨⎪⎪∑k∈Rδ(k)Rθ(kj)R,o(j)Y−t(j),k has input node jj is an output node, i.e. Q=Y∂E∂oQ(j)={∑k∈RδR(k)θR(kj),k has input node joY(j)−t(j),j is an output node, i.e. Q=Y

 

故有

 

δ(j)Q=∂E∂o(j)Q∂o(j)Q∂n(j)Q=∂E∂o(j)Qϕ′(n(j)Q)=⎧⎩⎨⎪⎪(∑k∈Rδ(k)Rθ(kj)R)ϕ′(n(j)Q),(o(j)Y−t(j))ϕ′(n(j)Y),k has input node jj is an output node, i.e. Q=YδQ(j)=∂E∂oQ(j)∂oQ(j)∂nQ(j)=∂E∂oQ(j)ϕ′(nQ(j))={(∑k∈RδR(k)θR(kj))ϕ′(nQ(j)),k has input node j(oY(j)−t(j))ϕ′(nY(j)),j is an output node, i.e. Q=Y

 

綜合以上各式，有梯度結果

 

∂E∂θ(ji)Q∂E∂b(j)Q=∂E∂o(j)Q∂o(j)Q∂n(j)Q∂n(j)Q∂θ(ji)Q=δ(j)Qo(i)P=∂E∂o(j)Q∂o(j)Q∂n(j)Q∂n(j)Q∂b(j)Q=δ(j)Q∂E∂θQ(ji)=∂E∂oQ(j)∂oQ(j)∂nQ(j)∂nQ(j)∂θQ(ji)=δQ(j)oP(i)∂E∂bQ(j)=∂E∂oQ(j)∂oQ(j)∂nQ(j)∂nQ(j)∂bQ(j)=δQ(j)

 

本來到這里應該就結束了，不過同正向的時候一樣，為了計算方便，我們依然希望能夠以矩陣或者向量的方式來表達。結論在這里：

假設有層 P,Q,RP,Q,R ，分別有 l,m,nl,m,n 個節點，依序前者輸出全連接到后者作為輸入。層 QQ 有權重矩陣 [ΘQ]m×l[ΘQ]m×l ，偏置向量 [bQ]m×1[bQ]m×1 ，層 RR 有權重矩陣 [ΘR]n×m[ΘR]n×m ，偏置向量 [bR]n×1[bR]n×1 。那么

 

∂E∂ΘQ∂E∂bQδQ=δQoTP=δQ={(ΘTRδR)∘ϕ′(nQ),(oY−t)∘ϕ′(nY),Q is a hidden layerQ=Y is the output layer∂E∂ΘQ=δQoPT∂E∂bQ=δQδQ={(ΘRTδR)∘ϕ′(nQ),Q is a hidden layer(oY−t)∘ϕ′(nY),Q=Y is the output layer

 

其中，運算 w=u∘vw=u∘v 表示 wi=uiviwi=uivi 。函數作用在向量或者矩陣上，表示作用在其每個分量上。

最后，補充幾個常用的激活函數的導數結果，推導很簡單，從略。

 

ϕ′(x)ϕ′(x)ϕ′(x)=sigmoid′(x)=sigmoid(x)(1−sigmoid(x))=oQ(1−oQ)=tanh′(x)=1−tanh2(x)=1−o2Q=softmax′(x)=softmax(x)−softmax2(x)=oQ−o2Qϕ′(x)=sigmoid′(x)=sigmoid(x)(1−sigmoid(x))=oQ(1−oQ)ϕ′(x)=tanh′(x)=1−tanh2(x)=1−oQ2ϕ′(x)=softmax′(x)=softmax(x)−softmax2(x)=oQ−oQ2

 

存在的問題

多層感知器存在的最大的問題就是，它是一個全連接的網絡，因此在輸入比較大的時候，權值會特別多。比如一個有1000個節點的隱層，連接到一個1000×1000的圖像上，那么就需要 10^9 個權值參數（外加1000個偏置參數）！這個問題，一方面限制了每層能夠容納的最大神經元數目，另一方面也限制了多層感知器的層數即深度。

多層感知器的另一個問題是梯度發散。 （這個問題的具體原因還沒有完全弄清楚，求指教！） 一般情況下，我們需要把輸入歸一化，而每個神經元的輸出在激活函數的作用下也是歸一化的；另外，有效的參數其絕對值也一般是小於1的；這樣，在BP過程中，多個小於1的數連乘，得到的會是更小的值。也就是說，在深度增加的情況下，從后傳播到前邊的殘差會越來越小，甚至對更新權值起不到幫助，從而失去訓練效果，使得前邊層的參數趨於隨機化（補充一下，其實隨機參數也是能一定程度上捕捉到圖像邊緣的）。

感謝shwley提供的幫助~

因為這些問題，神經元網絡在很長一段時間內都被冷落了。

從MLP到CNN

卷積神經網絡的名字怪嚇人，實際理解起來也挺嚇人的。哈哈，其實只要看明白了多層感知器的推導過程，理解卷積神經網絡就差不多可以信手拈來了。

摘要：首先解釋卷積神經網絡為什么會“長”成現在這般模樣。然后詳細推導了卷積神經網絡的預測過程和參數估計方法。

CNN的前世今生

既然多層感知器存在問題，那么卷積神經網絡的出現，就是為了解決它的問題。卷積神經網絡的核心出發點有三個。

• 局部感受野。形象地說，就是模仿你的眼睛，想想看，你在看東西的時候，目光是聚焦在一個相對很小的局部的吧？嚴格一些說，普通的多層感知器中，隱層節點會全連接到一個圖像的每個像素點上，而在卷積神經網絡中，每個隱層節點只連接到圖像某個足夠小局部的像素點上，從而大大減少需要訓練的權值參數。舉個栗子，依舊是1000×1000的圖像，使用10×10的感受野，那么每個神經元只需要100個權值參數；不幸的是，由於需要將輸入圖像掃描一遍，共需要991×991個神經元！參數數目減少了一個數量級，不過還是太多。
• 權值共享。形象地說，就如同你的某個神經中樞中的神經細胞，它們的結構、功能是相同的，甚至是可以互相替代的。也就是，在卷積神經網中，同一個卷積核內，所有的神經元的權值是相同的，從而大大減少需要訓練的參數。繼續上一個栗子，雖然需要991×991個神經元，但是它們的權值是共享的呀，所以還是只需要100個權值參數，以及1個偏置參數。從MLP的 10^9 到這里的100，就是這么狠！作為補充，在CNN中的每個隱藏，一般會有多個卷積核。
• 池化。形象地說，你先隨便看向遠方，然后閉上眼睛，你仍然記得看到了些什么，但是你能完全回憶起你剛剛看到的每一個細節嗎？同樣，在卷積神經網絡中，沒有必要一定就要對原圖像做處理，而是可以使用某種“壓縮”方法，這就是池化，也就是每次將原圖像卷積后，都通過一個下采樣的過程，來減小圖像的規模。以最大池化（Max Pooling）為例，1000×1000的圖像經過10×10的卷積核卷積后，得到的是991×991的特征圖，然后使用2×2的池化規模，即每4個點組成的小方塊中，取最大的一個作為輸出，最終得到的是496×496大小的特征圖。

現在來看，需要訓練參數過多的問題已經完美解決。 而梯度發散的問題，因為還不清楚具體緣由，依然留待討論。 關於梯度發散，因為多個神經元共享權值，因此它們也會對同一個權值進行修正，積少成多，積少成多，積少成多，從而一定程度上解決梯度發散的問題！

下面我們來揭開卷積神經網絡中“卷積”一詞的神秘面紗。

CNN的預測過程

回到開頭的圖1，卷積神經網絡的預測過程主要有四種操作：卷積、下采樣、光柵化、多層感知器預測。

卷積

先拋開卷積這個概念不管。為簡便起見，考慮一個大小為5×5的圖像，和一個3×3的卷積核。這里的卷積核共有9個參數，就記為 Θ=[θij]3×3Θ=[θij]3×3 吧。這種情況下，卷積核實際上有9個神經元，他們的輸出又組成一個3×3的矩陣，稱為特征圖。第一個神經元連接到圖像的第一個3×3的局部，第二個神經元則連接到第二個局部（注意，有重疊！就跟你的目光掃視時也是連續掃視一樣）。具體如圖2所示。

圖2的上方是第一個神經元的輸出，下方是第二個神經元的輸出。每個神經元的運算依舊是

 

f(x)=act(∑i,jnθ(n−i)(n−j)xij+b)f(x)=act(∑i,jnθ(n−i)(n−j)xij+b)

 

需要注意的是，平時我們在運算時，習慣使用 θijxijθijxij 這種寫法，但事實上，我們這里使用的是 θ(n−i)(n−j)xijθ(n−i)(n−j)xij ，原因馬上揭曉。

現在我們回憶一下離散卷積運算。假設有二維離散函數 f(x,y),g(x,y)f(x,y),g(x,y) ， 那么它們的卷積定義為

 

f(m,n)∗g(m,n)=∑u∞∑v∞f(u,v)g(m−u,n−v)f(m,n)∗g(m,n)=∑u∞∑v∞f(u,v)g(m−u,n−v)

 

現在發現了吧！上面例子中的9個神經元均完成輸出后，實際上等價於圖像和卷積核的卷積操作！這就是“卷積神經網絡”名稱的由來，也是為什么在神經元運算時使用 θ(n−i)(n−j)xijθ(n−i)(n−j)xij 。

如果你足夠細心，就會發現其實上述例子中的運算並不完全符合二維卷積的定義。實際上，我們需要用到的卷積操作有兩種模式：

• valid模式，用 ∗v∗v 表示。即上邊例子中的運算。在這種模式下，卷積只發生在被卷積的函數的定義域“內部”。一個 m×nm×n 的矩陣被一個 p×qp×q 的矩陣卷積（ m≥p,n≥qm≥p,n≥q ），得到的是一個 (m−p+1)×(n−q+1)(m−p+1)×(n−q+1) 的矩陣。
• full模式，用 ∗f∗f 表示。這種模式才是上邊二維卷積的定義。一個 m×nm×n 的矩陣被一個 p×qp×q 的矩陣卷積，得到的是一個 (m+p−1)×(n+q−1)(m+p−1)×(n+q−1) 的矩陣。

現在總結一下卷積過程。如果卷積層 cc 中的一個“神經中樞” jj 連接到特征圖 X1,X2,...,XiX1,X2,...,Xi ，且這個卷積核的權重矩陣為 ΘjΘj ，那么這個神經中樞的輸出為

 

Oj=ϕ(∑iXi∗vΘj+bj)Oj=ϕ(∑iXi∗vΘj+bj)

 

下采樣

下采樣，即池化，目的是減小特征圖，池化規模一般為2×2。常用的池化方法有：

• 最大池化（Max Pooling）。取4個點的最大值。這是最常用的池化方法。
• 均值池化（Mean Pooling）。取4個點的均值。
• 高斯池化。借鑒高斯模糊的方法。不常用。具體過程不是很清楚。。。
• 可訓練池化。訓練函數 ff ，接受4個點為輸入，出入1個點。不常用。

由於特征圖的變長不一定是2的倍數，所以在邊緣處理上也有兩種方案：

• 忽略邊緣。即將多出來的邊緣直接省去。
• 保留邊緣。即將特征圖的變長用0填充為2的倍數，然后再池化。一般使用這種方式。

對神經中樞 jj 的輸出 OjOj ，使用池化函數 downsample ，池化后的結果為

 

Sj=downsample(Oj)Sj=downsample(Oj)

 

光柵化

圖像經過池化-下采樣后，得到的是一系列的特征圖，而多層感知器接受的輸入是一個向量。因此需要將這些特征圖中的像素依次取出，排列成一個向量。具體說，對特征圖 X1,X2,...,XjX1,X2,...,Xj ，光柵化后得到的向量

 

ok=[x111,x112,...,x11n,x121,x122,...,x12n,...,x1mn,...,x2mn,...,xjmn]Tok=[x111,x112,...,x11n,x121,x122,...,x12n,...,x1mn,...,x2mn,...,xjmn]T

 

多層感知器預測

將光柵化后的向量連接到多層感知器即可。

CNN的參數估計

卷積神經網絡的參數估計依舊使用Back Propagation的方法，不過需要針對卷積神經網絡的特點進行一些修改。我們從高層到底層，逐層進行分析。

多層感知器層

使用多層感知器的參數估計方法，得到其最低的一個隱層 SS 的殘差向量 δsδs 。現在需要將這個殘差傳播到光柵化層 RR ，光柵化的時候並沒有對向量的值做修改，因此其激活函數為恆等函數，其導數為單位向量。

 

δR=(ΘTSδS)∘ϕ′(nR)=ΘTSδSδR=(ΘSTδS)∘ϕ′(nR)=ΘSTδS

 

光柵化層

從上一層傳過來的殘差為

 

δR=[δ111,δ112,...,δ11n,δ121,δ122,...,δ12n,...,δ1mn,...,δ2mn,...,δjmn]TδR=[δ111,δ112,...,δ11n,δ121,δ122,...,δ12n,...,δ1mn,...,δ2mn,...,δjmn]T

 

重新整理成為一系列的矩陣即可，若上一層 QQ 有 qq 個池化核，則傳播到池化層的殘差

 

ΔQ=Δ1,Δ2,...,ΔqΔQ=Δ1,Δ2,...,Δq

 

池化層

對應池化過程中常用的兩種池化方案，這里反傳殘差的時候也有兩種上采樣方案：

• 最大池化：將1個點的殘差直接拷貝到4個點上。
• 均值池化：將1個點的殘差平均到4個點上。

即傳播到卷積層的殘差

 

Δp=upsample(Δq)Δp=upsample(Δq)

 

卷積層

卷積層有參數，所以卷積層的反傳過程有兩個任務，一是更新權值，另一是反傳殘差。先看更新權值，即梯度的推導。

如圖三上方，先考慮卷積層的某個“神經中樞”中的第一個神經元。根據多層感知器的梯度公式

 

∂E∂θji=δjoi∂E∂θji=δjoi

 

那么在圖三上方的例子中，有

 

∂E∂θ11=δ11o22∂E∂θ12=δ11o21∂E∂θ21=δ11o12∂E∂θ22=δ11o11∂E∂θ11=δ11o22∂E∂θ12=δ11o21∂E∂θ21=δ11o12∂E∂θ22=δ11o11

 

考慮到其他的神經元，每次更新的都是這四個權值，因此實際上等價於一次更新這些偏導數的和。如果僅考慮對 θ11θ11 的偏導數，不難發現如圖3下方所示，其值應該來自於淡藍色和灰色區域。是不是似曾相識？是的，又是卷積！但是又有兩處重要的不同：

• 在計算對 θ11θ11 的偏導數時，淡藍色區域和灰色區域的對應位置做運算，但是在卷積運算中，這些位置應該是旋轉過來的！
• θ11θ11 在 ΘΘ 矩陣的左上角，而淡藍色區域在右下角，同樣是旋轉過的！

因此，對卷積層 PP 中的某個“神經中樞” pp， 權值（以及偏置，不再具體推導）更新公式應該是

 

∂E∂Θp∂E∂bp=rot180((∑q′Oq′)∗vrot180(Δp))=∑u,v(δp)uv∂E∂Θp=rot180((∑q′Oq′)∗vrot180(Δp))∂E∂bp=∑u,v(δp)uv

 

其中，rot180rot180 是將一個矩陣旋轉180度； Oq′Oq′ 是連接到該“神經中樞”前的池化層的輸出；對偏置的梯度即 ΔpΔp 所有元素之和。

下面討論殘差反傳的問題。

如圖4，考慮淡藍色像素點影響到的神經元，在這個例子中，受影響的神經元有4個，他們分別以某個權值與淡藍色像素運算后影響到對應位置的輸出。再結合多層感知器的殘差傳播公式，不難發現這里又是一個卷積過程！同樣需要注意的是，正如圖4中的數字標號，這里的卷積是旋轉過的；另外，這里用的卷積模式是full。

如果前邊的池化層 Q′Q′ 的某個特征圖 q′q′ 連接到這個卷積層 PP 中的某“神經中樞”集合 CC ，那么傳播到 q′q′ 的殘差為

 

Δq′=(∑p∈CΔp∗frot180(Θp))∘ϕ′(Oq′)Δq′=(∑p∈CΔp∗frot180(Θp))∘ϕ′(Oq′)

 

最后一公里：Softmax

前邊我有意忽略了對Softmax的討論，在這里補上。因為Softmax的資料已經非常多了，所以這里不再詳細討論。具體可以參考這篇文章。

需要補充說明的是，不難發現，Softmax的梯度公式與多層感知器的BP過程是兼容的；另外，實現Softmax的時候，如果需要分為 kk個類，同樣也可以設置 kk 個輸出節點，這相當於隱含了一個類別名稱為“其他”的類。

CNN的實現

我建立了一個Github的repo，目前內容還是空的，近期會逐漸上傳。

思路

以層為單位，分別實現卷積層、池化層、光柵化層、MLP隱層、Softmax層這五個層的類。其中每個類都有output和backpropagate這兩個方法。

另外，還需要一系列的輔助方法，包括：conv2d（二維離散卷積，valid和full模式），downsample（池化中需要的下采樣，兩種邊界模式），upsample（池化中的上采樣），以及dsigmoid和dtanh等。

其他

還需要考慮的是可擴展性和性能優化，這些以后再談~

 

from: http://www.moonshile.com/post/juan-ji-shen-jing-wang-luo-quan-mian-jie-xi