A*尋路算法

寫在前面的話

---

無意中在cocoaChina的首頁看到了一篇介紹A*算法用swift實現的文章，對A*尋路算法產生了興趣。在百度谷歌了很多文章后，終於A*算法的流程，同時讓我發現了兩篇非常好的英文文章：

A* Pathfinding for Beginners

Introduction to A*

第一篇文章是非常好的A*算法入門文章，通讀一遍就基本可以用代碼實現了；第二篇文章可以說給我帶來了震撼，原來算法可以這樣講，推薦大家都看一下。

看完第二篇文章就產生了要學習作者的方式講一下A*算法的沖動，同時也當是練練手，好久沒寫javaScript了。

講解方式也按照<Introduction to A*>一文中的順序，從最簡單的廣度優先算法(Breadth-First-Search)、大名鼎鼎的Dijkstra算法到Greed-Best-First-Search算法，最后是A*算法。

（關於A*算法，網上資料很多，A*算法的變種也很多，有興趣的朋友可以自行搜索，
本文僅對四種常見尋路算法進行簡單介紹，若有不合理或錯誤之處，請諒解並在回復中指出）

廣度優先算法

---

廣度優先算法是最簡單的尋路算法，算法執行的結果是獲得從地圖上任意一點S到其他所有可達點的最短路徑，這里只考慮上下左右四方向行走的情況，算法流程非常容易理解：

1. 設定搜索起點S，放入openList中；
2. 判斷openList是否為空，若為空，搜索結束；若不為空，拿出openList中的第一個節點G；
3. 遍歷G的上下左右四個相鄰節點N1-N4，對每個節點N，如果N不在openList或closeList中，那么令N的父節點為G，將N放入openList中；如果N已經在openList或closeList中，跳過不處理；
4. 將G放入closeList中，重復步驟2.

演示gif：

演示程序

藍色方塊是不可通過的，S為掃描的起始點，一層層向外擴展，最終所有可到達的節點都被掃描，這一過程有時被稱為“flood fill”。對於每一個被掃描的節點，為其添加一個指向父節點的方向箭頭，然后你會發現，從地圖上任意一點開始，只要沿着箭頭的方向移動，總能走到起始點S，而且走過的路徑必然是最短路徑之一。

看到廣度優先算法，最先想到的應用場景就是塔防，敵人總是從固定的一個或幾個出生點出現，向着固定的一個或幾個目標移動，我們完全可以在每一關開始前以出生點為起始點遍歷整個地圖，這樣本關中怪物的移動路線就可以確定了。

下面讓我們考慮以下場景，地圖中存在森林、山嶺和平原，角色在這些地形上移動時，移動力消耗是不同的，比如《文明》中。這就要求我們把每一個區塊的消耗考慮在內，這時，Dijkstra算法就可以發揮作用了。

Dijkstra算法

---

在地圖內的每個區塊移動消耗不同時，Dijkstra算法可以非常方便的找出從地圖上某個起始區塊到其他所有可達區塊的最短路徑，這里仍然只考慮上下左右四個方向移動的情況，算法流程如下：

說明：起始區塊記作S，從S到當前區塊G的總移動消耗記作CG，優先隊列openList中數據為(G,CG)（區塊，S到當前區塊總移動消耗）,區塊G自身移動消耗記作ZG。

1. 設定起始區塊S，將區塊S和總移動消耗C=0（記作(S,0)）放入openList，其中openList是一個優先隊列(PriorityQueue)，總移動消耗C越低優先級越高；
2. 判斷openList是否為空，如果是空，算法結束；否則，從openList中拿出優先級最高的區塊G；
3. 遍歷G的上下左右四個相鄰區塊N1-N4，對每個區塊N，如果N已經在closeList中，忽略該區塊；如果N不可達，忽略該區塊；否則會有兩種情況:
   1. 如果N不在openList中，那么將(N,CN)放入openList中，其中CN=CG+ZN,既S到N的移動總消耗等於S到G的移動總消耗加上N本身的移動消耗，令N的父節點為G;
   2. 如果N已經在openList中，取出(N,CN)，仍然計算CN1=CG+ZN，如果CN1小於CN，用(N,CN1)替換openList中的(N,CN)，令N的父節點為G；如果CN1大於或等於CN，不做處理。
4. 重復步驟2直至算法結束。

演示gif ：

演示程序

藍色區域不可通過，白色區塊代表平原地形，移動一格消耗為1，綠色區塊代表森林，移動一格消耗為5，黑色區塊帶表山脈，移動一格消耗為10。區塊中的數字表示從起始點到當前區塊的最小移動消耗。從演示程序可以看出，由於優先隊列的存在，區塊消耗越高，進入closeList的時間越靠后，這與廣度優先算法中一層層向外擴展的方式不同。

不難想到，當地圖上的所有區塊移動消耗相同時，Dijkstra算法就簡化為廣度優先算法，因為移動總消耗最低的區塊總會是當前區塊的相鄰區塊。

在《Introduction to A*》中，作者提出了一個非常有趣的Dijkstra算法的應用，在這里和大家分享下：在某個游戲中，當我希望我的角色更傾向於經過某些區塊時（比如經過這些區塊可以獲得增益效果、道具等等）或者傾向於躲避某些區塊時（比如經過這些區塊會丟失生命值，或者這些區塊上的敵人非常危險），我們可以通過調整這些區塊的移動消耗來影響移動路徑的產生從而影響角色的移動行為。一片區域上的移動消耗很小時，算法生成的最短路徑會傾向於經過這片區域，如gif中要到達森林區塊的右側時，路徑沒有橫穿森林，而是繞着森林邊緣走的，反之亦然。

廣度優先算法和Dijkstra算法都需要遍歷整個地圖，而在大多數場景中，我們只需要知道一個點到另一個點的最短路徑，下面的Greed-Best-First-Search為我們提供了一個思路。

Greed-Best-First-Search

網上沒有找到比較官方的翻譯，有人譯作“最好優先貪婪算法”，我們暫時這么稱呼它。

最好優先貪婪算法與上面兩種算法的不同之處在於，它總是嘗試向離目標節點更近的方向探索，怎樣才算離目標節點更近呢？在只能上下左右四方向移動的前提下，我們通過計算當前節點到目標節點的曼哈頓距離來進行判斷。

假設當前節點坐標為(x,y)，目標節點的坐標為(x1,y1)，曼哈頓距離計算公式如下：

Manhattan_distance = abs(x1-x)+abs(y1-y)

由於曼哈頓距離只在兩點之間沒有障礙物的情況下才與實際距離相等，一般情況下曼哈頓距離總是小於實際距離。因此，當節點間不存在障礙物時，算法可以保證找出最短路徑，但是一旦障礙物出現，最短路徑就無法保證了。

算法流程如下：

說明：起始節點記作S，目標節點記作E，對於任意節點G，從當前節點G到目標節點E的曼哈頓距離記作MG，優先隊列openList中數據為(G,MG)（節點，當前節點到目標節點E的曼哈頓距離）。

1. 將起始節點S放入openList，openList是一個優先隊列，曼哈頓距離越小的節點，優先級越高。
2. 判斷openList是否為空，如果為空，搜索失敗，目標節點E不可達；如果不為空，從openList中拿出優先級最高的節點G;
3. 遍歷節點G的上下左右四個相鄰節點N1-N4，如果N在openList或closeList中，忽略節點N；否則，令N的父節點為G，計算N到E的曼哈頓距離MN，將(N,MN)放入openList。
4. 判斷節點G是不是目標節點E，如果是，搜索成功，獲取節點G的父節點，並遞歸這一過程（繼續獲得父節點的父節點），直至找到初始節點S，從而獲得從G到S的一條路徑；否則，重復步驟2。

演示gif：

演示程序

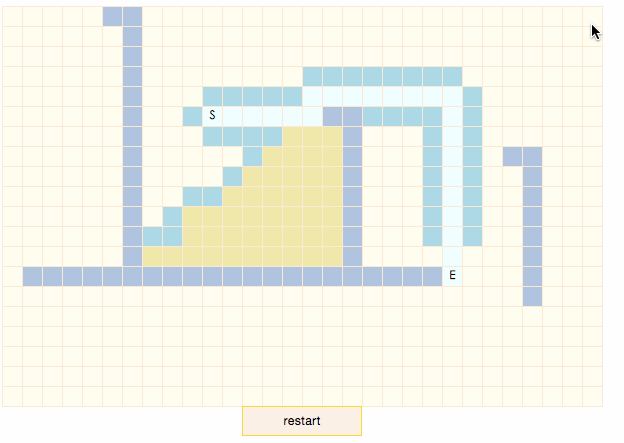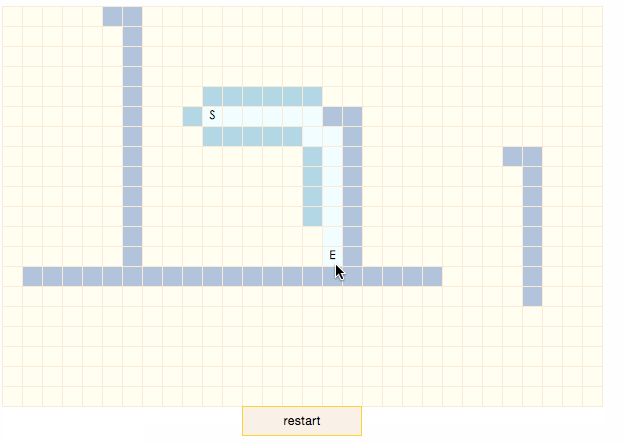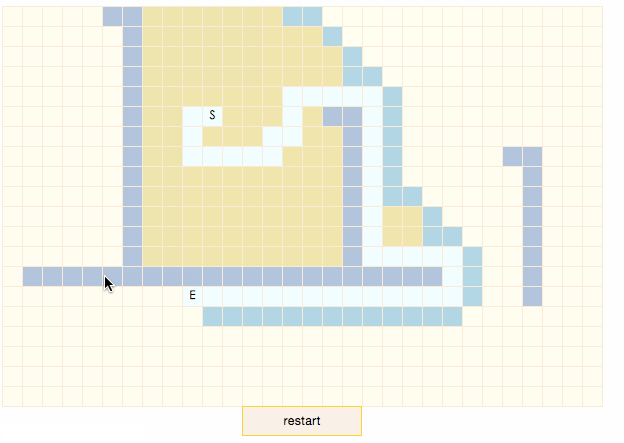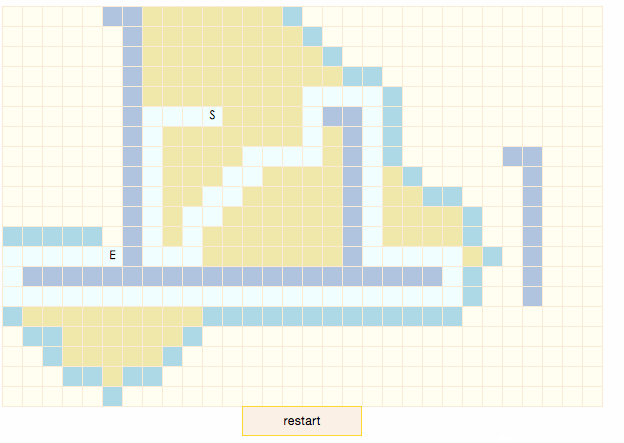
演示程序中，暗藍色表示節點是障礙物，土黃色表示節點處於closeList中，淡藍色表示節點處於openList中，白色表示節點處於搜索出的結果路徑上。點擊地圖上的區塊可以重新設置目標節點E。可以看出，當目標節點處於地圖左下方時，搜索路徑很明顯不是最短路徑。雖然算法不能保證可以找到最短路徑，但當地形不復雜時（如gif中起點和終點間沒有障礙物），路徑搜索速度是四種算法中最快的。

最好優先貪婪算法雖然不能保證找出最短路徑，但為我們提供了一個思路，A*算法就是Dijkstra算法與最好優先貪婪算法結合后得到的算法。

A*算法

---

A*算法與最好優先貪婪算法一樣都通過計算一個值來判斷探索的方向。對於節點N，計算公式如下：

F(N)=G(N)+H(N)

其中G(N)就是Dijkstra算法中計算的，從起點到當前節點N的移動消耗，而H(N)，在只允許上下左右移動的前提下，就是最好優先貪婪算法中當前節點N到目標節點E的曼哈頓距離。因此，當節點間移動消耗非常小時，G對F的影響也會微乎其微，A*算法就退化為最好優先貪婪算法；當節點間移動消耗非常大以至於H對F的影響微乎其微時，A*算法就退化為Dijkstra算法。

算法流程如下：

說明：起始節點記作S，目標節點記作E，對於任意節點P，從S到當前節點P的總移動消耗記作GP，節點P到目標E的曼哈頓距離記作HP，從節點P到相鄰節點N的移動消耗記作DPN，用於優先級排序的值F(N)記作FP。

1. 選擇起始節點S和目標節點E，將(S,0)（節點，節點F(N)值）放入openList，openList是一個優先隊列，節點F(N)值越小，優先級越高。
2. 判斷openList是否為空，若為空，則搜索失敗，目標節點不可達；否則，取出openList中優先級最高的節點P;
3. 遍歷P的上下左右四個相鄰接點N1-N4，對每個節點N，如果N已經在closeList中，忽略；否則有兩種情況，
   • 如果N不在openList中，令GN=GP+DPN，計算N到E的曼哈頓距離HN，令FN=GN+HN，令N的父節點為P，將(N,FN)放入openList；
   • 如果N已經在openList中，計算GN1= GP+DPN，如果GN1小於GN，那么用新的GN1替換GN，重新計算FN，用新的(N,FN)替換openList中舊的(N,FN)，令N的父節點為P；如果GN1不小於GN，不作處理。
4. 將節點P放入closeList中。判斷節點P是不是目標節點E，如果是，搜索成功，獲取節點P的父節點，並遞歸這一過程（繼續獲得父節點的父節點），直至找到初始節點S，從而獲得從P到S的一條路徑；否則，重復步驟2;

演示gif：

演示程序

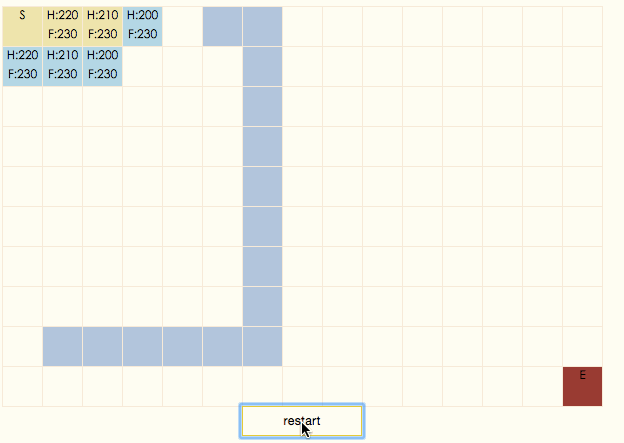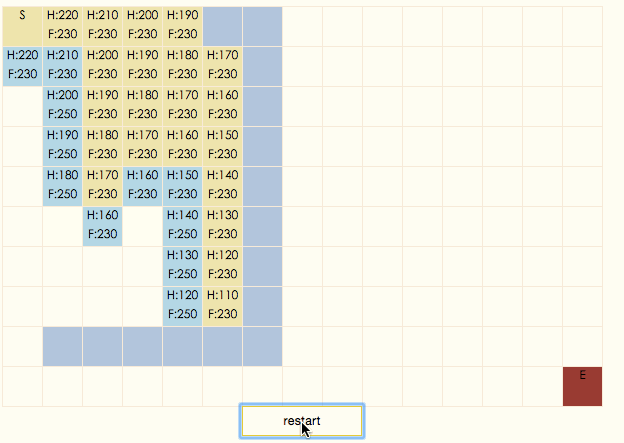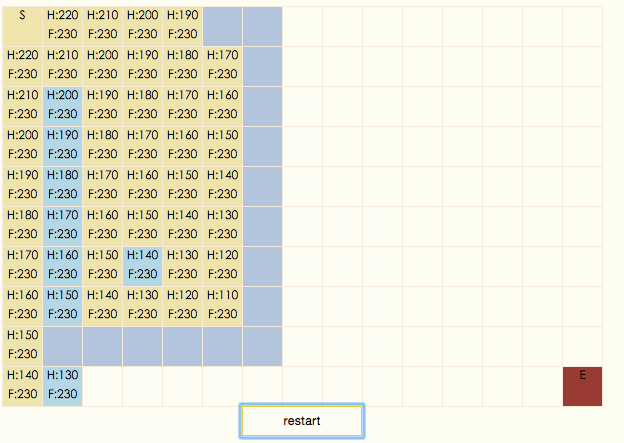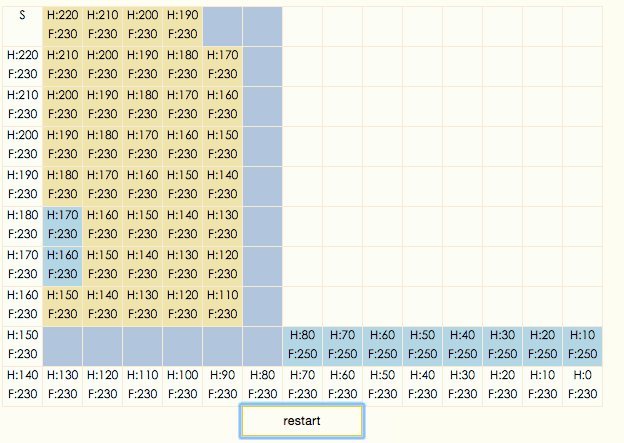
演示gif中，土黃色表示節點在closeList中，淡藍色表示節點在openList中，深藍色表示節點不可通過，白色表示節點在搜索出的結果路徑上。可以看出，A*算法總是設法保證搜索路徑上的F值保持不變。

在繼續測試演示程序時，我發現了一個問題：

由於我用JS開發的上述演示程序，沒有趁手的優先隊列，所以用Array客串了一把，每次取值時根據F值進行倒序排序，取隊列末尾的值。從gif中可以看出，算法執行的並不完美，我們當然希望A*算法在簡單環境下能夠擁有和最好優先貪婪算法一樣的運行速度，但我的A*算法卻出現了無用的掃描，並不在搜索結果上的區域也參與了計算。怎樣避免這一情況呢？

首先想到的當然是改進我的優先隊列，但這有點麻煩啊，別着急，有更簡單的方法，這個方法和接下來要了解的啟發式算法有關。

關於最優選擇貪婪算法和A*算法中的曼哈頓距離的運用屬於啟發式算法(Heuristic Algrathm)的一種，這也是A*算法公式F=G+H中H的由來。

這里摘抄一段《Introduction to A*》的作者在另一篇文章《Heuristic》中的一小段，講述H(n)如何影響A*算法的行為。

At one extreme, if h(n) is 0, then only g(n) plays a role, and A* turns into Dijkstra’s algorithm, which is guaranteed to find a shortest path.
If h(n) is always lower than (or equal to) the cost of moving from n to the goal, then A* is guaranteed to find a shortest path. The lower h(n) is, the more node A* expands, making it slower.
If h(n) is exactly equal to the cost of moving from n to the goal, then A* will only follow the best path and never expand anything else, making it very fast. Although you can’t make this happen in all cases, you can make it exact in some special cases. It’s nice to know that given perfect information, A* will behave perfectly.
If h(n) is sometimes greater than the cost of moving from n to the goal, then A* is not guaranteed to find a shortest path, but it can run faster.
At the other extreme, if h(n) is very high relative to g(n), then only h(n) plays a role, and A* turns into Greedy Best-First-Search.

翻譯如下：

1. 一種極端情況是，當H(n)=0時，只有G(0)有效，此時A*算法變為Dijkstra算法，可以保證找到最短路徑。
2. 如果H(n)總能保證不大於從n到終點的實際距離，那么A*算法就可以保證找到最短路徑（如上面演示程序中，在智能上下左右四方向移動的前提下，曼哈頓距離總是小於或等於實際距離）。H(n)相比實際距離越小，A*算法需要探索的節點就更多，性能就會更差一些。
3. 如果H(n)與n到終點的實際距離相等，那么A*算法就可以一直保持探索路徑在最優路徑上而不需要探索額外的節點，使得算法執行非常快。雖然這是理想狀態下的場景，但是如果提前對地圖進行分析，我們還是可以保證A*算法在近似理想的狀態下工作。（關於A*算法的優化后面會講到）
4. 另一種極端情況是，當H(n)相對於G(n)非常大時，只有H(n)有效，A*算法就會變成最優選擇貪婪算法，不能保證找到最短路徑。

回到剛才的問題，這個簡單的方法就是修改我們的H(n)，新的曼哈頓距離公式為

Manhattan_distance = abs(x1-x)+abs(y1-y)*1.01

我們對上下方向的距離進行了輕微的調整，效果如何呢？

演示程序

允許斜方向移動演示程序

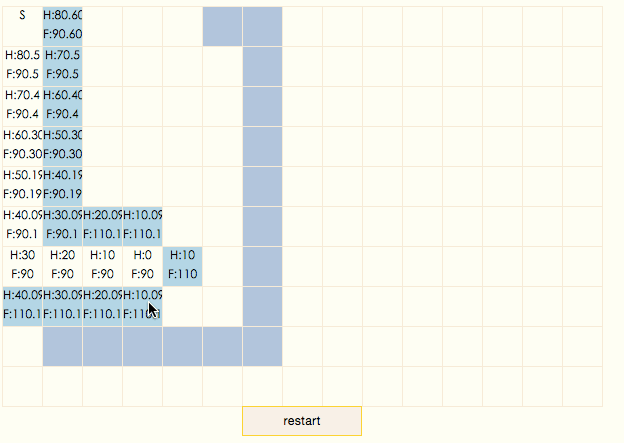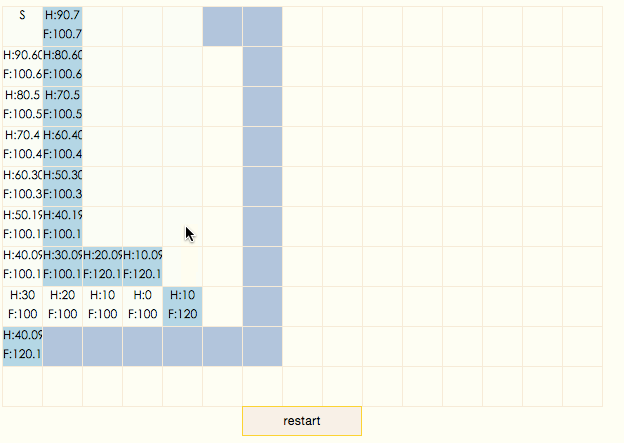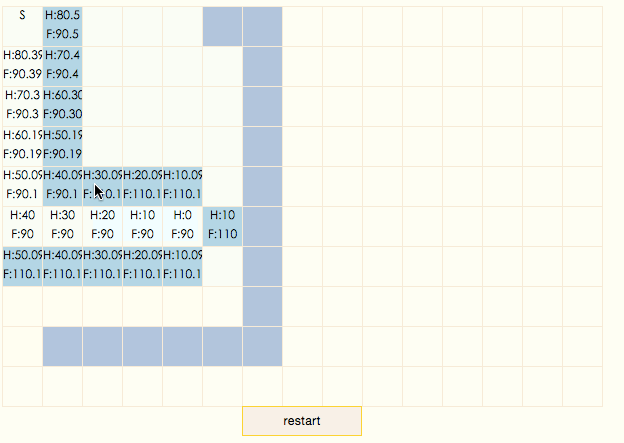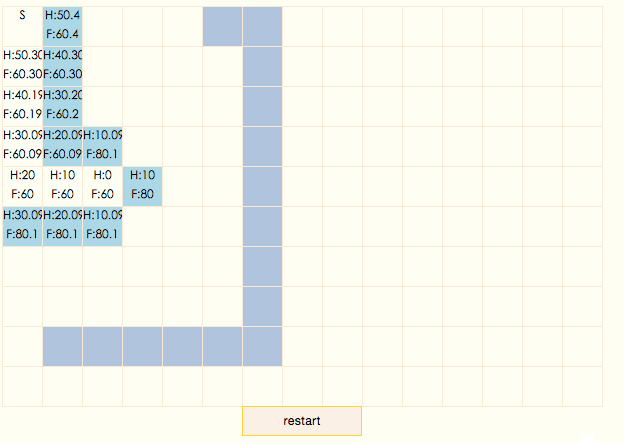
可以看到，掃描過程非常高效，所有closeList中的節點都出現在了結果路徑上。這是因為A*算法會沿着F值變小的方向搜索，由於曼哈頓公式的調整，原本F值相等的節點不再想等，同一列由上到下遞減，這就產生了gif中的現象，結果路徑總是先向下走，直到和目標節點同一行后，再向右走。

關於四種算法的選擇

1. 雖然最優選擇貪婪算法只在特定情況下才可以找到最短路徑（沒有障礙物、沒有地形移動消耗差異），但是它的運行速度是最快的。如果情況允許，優先使用本算法。
2. 當需要知道地圖上某個點到所有其他點的最短路徑，或者反過來，地圖上所有點到某個點的最短路徑時，選擇廣度優先算法（各區塊移動消耗相同）或Dijkstra算法（各區塊移動消耗不同）。
3. 在一般情況下，使用A*算法總是正確的。

A*算法的一般優化

---

在情況允許的前提下，在生成地圖或者加載地圖時，記錄地圖上的特征區域。特征區域分為兩類：

• 第一類是不可到達區域，當目標點位於不可到達區域時，以上四類算法都會進行全圖掃描，這絕對是資源的極大浪費；
• 第二類是導航點，所謂導航點，就是地圖上兩個區域間移動的必經之路，例如游戲中兩片陸地被河流分割，中間一座小橋，這座橋就是導航點，當需要找到從一片大陸到另一片大陸的最短路徑時，可以先算出起點到這座橋的最短路徑，再算出這座橋到終點的最短路徑，那么兩者加起來就是起點到終點的最短路徑。同樣的道理，如果地圖分為兩層，樓梯的部分也是導航點。