本文是对于北京大学熊英飞老师《软件分析》课件以及南京大学李樾老师《软件分析》课程视频的总结。
1.哥德尔不完备定理及其在软件分析中应用
1.1定理内容
对任意能表示自然数的系统,一定有定理不能 被证明
1.2定理应用
主流程序语言的语法+语义=能表示自然数的形式系统 。
哥德尔不完备定理在处理内存泄露判定问题时的应用
设有表达式T不能被证明
a=malloc()
if (T) free(a);
return;
若T为永真式,则没有内存泄露,否则就可能有。
2.停机问题
2.1停机问题内容
停机问题的实质是判断一个程序在给定输入上是否会终止 ,不存在一个算法能回答停机问题。
2.2停机问题实例
假设存在停机问题判断算法:bool Halt(p) ,p为特定程序,给定某邪恶程序
void Evil() {
if (!Halt(Evil)) return;
else while(1);
}
Halt(Evil)的返回值是什么?
• 如果为真,则Evil不停机,矛盾
• 如果为假,则Evil停机,矛盾
2.3一个检查停机问题的算法
当前系统的状态为内存和寄存器中所有Bit的值 ,给定任意状态,系统的下一状态是确定的 。令系统的所有可能的状态为节点,状态A可达状态B 就添加一条A到B的边,那么形成一个有向图(有限 状态自动机),如果从任意初始状态出发的路径都无环,那么系统 一定停机,否则可能会死机 ,给定起始状态,遍历执行路径,同时记录所有访问过的状 态。 如果有达到一个之前访问过的状态,则有环。如果达到终 态,则无环。 因为状态数量有穷,所以该算法一定终止。
3.可判定问题
判定问题(Decision Problem):回答是/否的问题
可判定问题(Decidable Problem)是一个判定问题,该问题存在一个算法,使得对于该问题的每 一个实例都能给出是/否的答案。
停机问题是不可判定问题
4.莱斯定理(Rice’s Theorem)
4.1定理内容
我们可以把任意程序看成一个从输入到输出上的 部分函数(Partial Function),该函数描述了程序的行为 。
关于程序行为的任何非平凡属性,都不存在可以 检查该属性的通用算法
- 平凡属性:要么对全体程序都为真,要么对全体程序 都为假
- 非平凡属性:不是平凡的所有属性
- 关于程序行为:即能定义在函数上的属性
- 特别注意莱斯定理的适用条件是关于程序行为而不是结构,并且不适用莱斯定理的也未必可判定。例如程序使用了多少个变量,就是涉及程序结构的问题,所以像[确定程序使用的变量是否多于50个]这样的问题无法用莱斯定义来说明它是不是不可判定的。
4.2莱斯定理的证明
反证法:给定函数上的性质P,因为P非平凡,所以一定存在程序使 得P满足,记为ok_prog。假设检测该性质P的算法为P_holds。
编写如下函数来检测程序p是否停机
Bool halt(Program p) {
void evil(Input n) {
Output v = ok_prog(n);
p();
return v;
}
return P_holds(evil);
}
如果P_holds存在,则我们有了检测停机的算法
5.近似法
5.1定义
近似法:允许在得不到精确值的时候,给出不精确的答案。对于判断问题,不精确的答案就是不知道。
近似求解判定问题:输出“是”、“否”或者“不 知道”,我们的目标就是尽可能多的回答“是”、“否”,尽可能少的回答“不知道”。
5.2分类
假设正确答案是一个集合S
-
must分析:返回的集合总是S的子集
-
may分析:返回的集合总是S的超集
must和may的区分并不严格,可以互相转换 ,可以将判定问题取反,或者队友返回集合的问题,将返回值定义为原集合的补集。
6.软件分析的评定标准
在编译器优化中,我们需要保证决定不改变程序的语义 。安全性就是根据分析结果所做的优化绝对不会改变程序语义 。安全性的定义和具体应用场景有关,但往往对应于 must分析和may分析中的一个 。安全性有时也被成为健壮性(soundness)、正确性 (correctness) 。 健壮性的反面有时也被称为完整性(completeness) ,如果健壮性对应must-analysis,则完整性对应may-analysis。
根据莱斯定理,现实中不存在既sound又complete(即下图中的truth的分析)

如上图,我们举例来理解这几个概念,假设一个程序中某错误有十个,分别是a、b、c、d...等等,这是个错误叫做truth,sound就是找到了不小于十个的错误,这其中包含了真实的这十个,我们称之为overapproximate,也就是过近似。而complete就是找到错误的数量不大于十个,但是能保证所有找到的都是真实的错误,我们称之为underapproximate。
软件分析的目的并不是求完美解(也求不到),我们的目的是求最优解,因此会产生两种情况:
- 妥协soundness(false negatives漏报)
- 妥协completeness(false positives误报)
绝大多数软件分析都是妥协completeness,所以从静态分析角度只要满足soundness就是正确的。
7.软件分析求解过程
软件分析求解过程分为两步,分别是abstraction和safe-approximation.
- Abstraction:符号分析里的简单例子,可以将变量值抽象为正负零以及未知和未定义
- Safe-approximation(Over-approximation)
- Transfer functions
- Control flows
8.控制流分析
控制流分析主要是通过控制流图来实现的。控制流图中的每个节点可以是一条单独的三地址指令也可以(或者说大多数情况下)是一个基本块(Basic Block,简称BB)。
8.1控制流图中的基本块
基本块是连续的三地址指令的集合,它满足以下条件:
- 每个BB只有一个入口,且必为该BB的第一条语句。
- 每个BB的出口必为该BB的最后一条语句。
下面是一个BB分析的实录

方法:先将第一句和最后一句指令分别作为所在块的入口及出口,接下来找出所有的跳转语句,将它们作为所在BB的最后一句,再将这些跳转语句的目标语句作为所在BB的第一句,以此切分出BB来。结果如下:

8.2控制流图
控制流图中的节点就是基本块
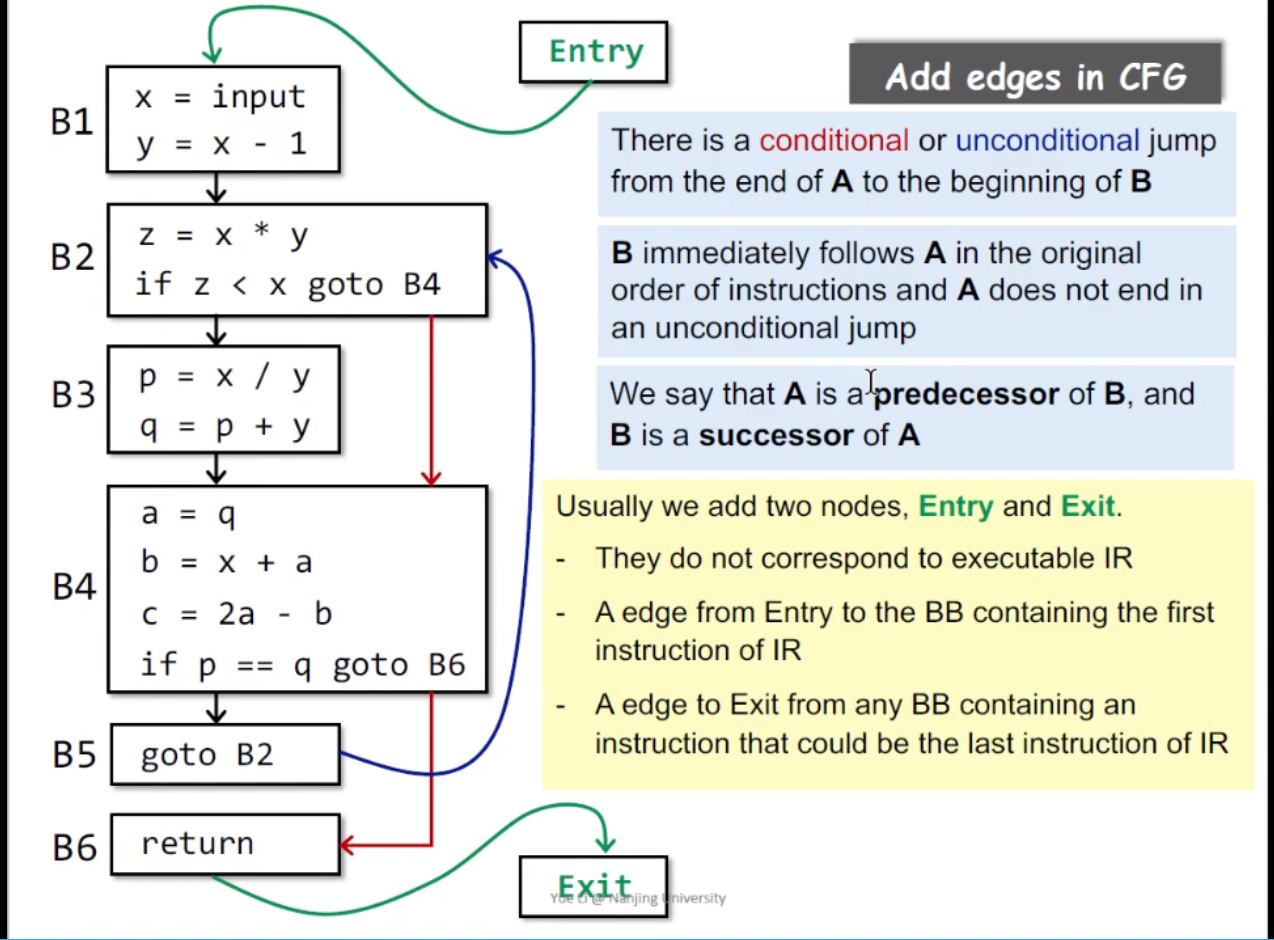
从基本块A到基本块B中间右边的条件是:
- 从块A的出口到块B的入口之间有条件性或者无条件性的跳转。
- A的出口指令是一个无条件的goto(),这样A到B之间就没有边。
- 条件Jump Block天然有两个出口,这取决于条件值是否为真。
我们经常将指令间的跳转转化为基本块间的跳转,关于以上的内容的总结如下图: