目的
求一个实对称矩阵的所有特征值和特征向量。
前置知识
对于一个实对称矩阵\(A\),必存在对角阵\(D\)和正交阵\(U\)满足$$D=U^TAU$$\(D\)的对角线元素为\(A\)的特征值,\(U\)的列向量为\(A\)的特征向量。
定义\(n\)阶旋转矩阵$$G(p,q,\theta)=
\begin{bmatrix}
1 & & & & & \cdots& & & & & 0\
&\ddots & & & & & & & & &\
& &1 & & & & & & & &\
& & &\cos\theta & & & &-\sin\theta & & &\
& & & &1 & &0 & & & &\
& & & & &\ddots & & & & &\
& & & &0 & &1 & & & &\
& & &\sin\theta & & & &\cos\theta & & &\
& & & & & & & &1 & &\
& & & & & & & & &\ddots &\
0& & & & & & & &0 & &1
\end{bmatrix}
\[即在单位矩阵的基础上,修改$a_{pp}=a_{qq}=\cos\theta,a_{qp}=-a_{pq}=\sin\theta$ 对于$n$阶向量$\alpha$,$\alpha\cdot G(p,q,\theta)$的几何意义是把$\alpha$在与第$p$维坐标轴和第$q$维坐标轴平行的平面内旋转角度$\theta$,并且旋转后的模长保持不变。 ## 算法原理 大概思路使通过旋转变换使非对角线上的元素不断变小,最后得到与原矩阵相似的对角矩阵。 每次找到矩阵$A$绝对值最大的的非对角线元素,设为$a_{pq}$,令$U=G(p,q,\theta)$,将$A$变换为$U^TAU$ 变换后的值为 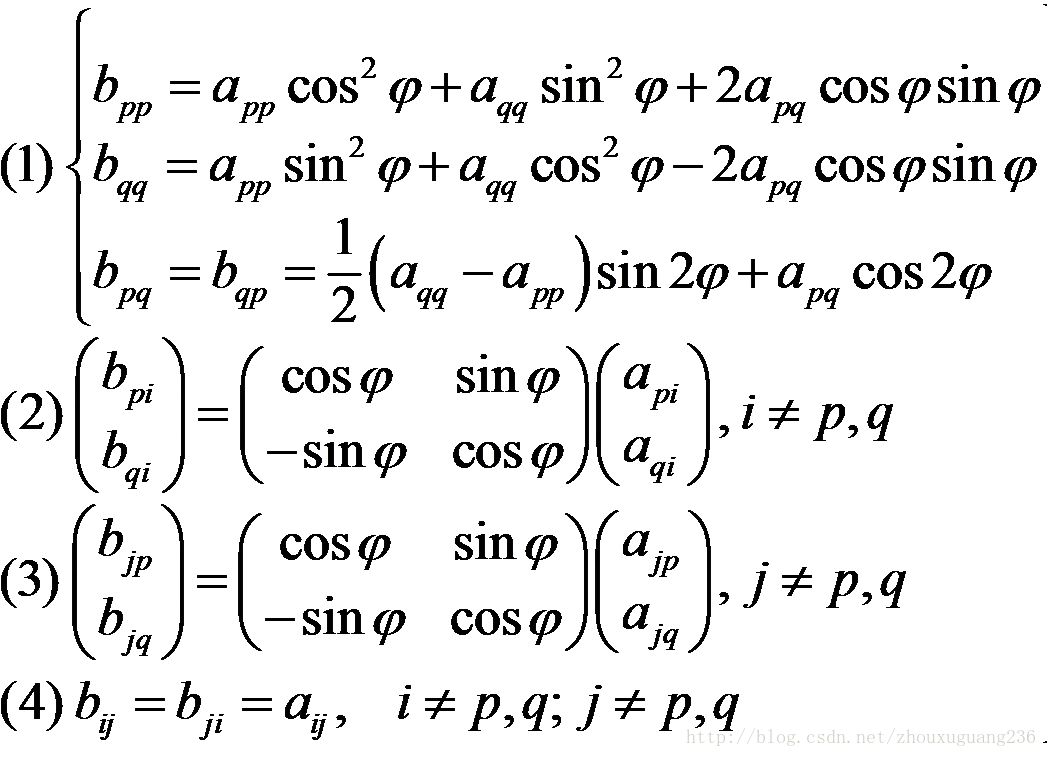 通过令$b_{p,q}=0$解得$$\theta=\frac{1}{2}\arctan\frac{2a_{pq}}{a_{qq}-a_{pp}}$$特别地当$a_{qq}=a_{pp}$时$\theta=\frac{\pi}{4}$ 注意到旋转操作并不会改变每个行向量或列向量的模长,即矩阵$A$的F-范数$||A||_F=\sqrt{\sum_i\sum_ja_{ij}^2}$是不变的,并且通过计算可以得出$$b_{ip}^2+b_{iq}^2=a_{ip}^2+a_{iq}^2$$从而可以得知非对角线元素的平方和变小,对角线上元素的平方和增大,故非主对角线上元素的平方和收敛。 ## 算法流程 (1)令矩阵$T=E$,即初始化单位矩阵 (2)找到$A$中绝对值最大的非对角选元素$a_{pq}$ (3)找到对应的角度$\theta$,构造矩阵$U=G(p,q,\theta)$ (4)令$A=U^TAU,T=TU$ (5)不停地重复(2)到(4),直到$a_{pq}<\epsilon$或迭代次数超过某个限定值,则$A$的对角线元素近似等于$A$的特征值,$T$的列向量为$A$的特征向量 ## 代码 ```c #include<bits/stdc++.h> using namespace std; const int N=1005; const double eps=1e-5; const int lim=100; int n,id[N]; double key[N],mat[N][N],EigVal[N],EigVec[N][N],tmpEigVec[N][N]; bool cmpEigVal(int x,int y) { return key[x]>key[y]; } void Find_Eigen(int n,double (*a)[N],double *EigVal,double (*EigVec)[N]) { for (int i=1;i<=n;i++) for (int j=1;j<=n;j++) EigVec[i][j]=0; for (int i=1;i<=n;i++) EigVec[i][i]=1.0; int count=0; while (1) { //统计迭代次数 count++; //找绝对值最大的元素 double mx_val=0; int row_id,col_id; for (int i=1;i<n;i++) for (int j=i+1;j<=n;j++) if (fabs(a[i][j])>mx_val) mx_val=fabs(a[i][j]),row_id=i,col_id=j; if (mx_val<eps||count>lim) break; //进行旋转变换 int p=row_id,q=col_id; double Apq=a[p][q],App=a[p][p],Aqq=a[q][q]; double theta=0.5*atan2(-2.0*Apq,Aqq-App); double sint=sin(theta),cost=cos(theta); double sin2t=sin(2.0*theta),cos2t=cos(2.0*theta); a[p][p]=App*cost*cost+Aqq*sint*sint+2.0*Apq*cost*sint; a[q][q]=App*sint*sint+Aqq*cost*cost-2.0*Apq*cost*sint; a[p][q]=a[q][p]=0.5*(Aqq-App)*sin2t+Apq*cos2t; for (int i=1;i<=n;i++) if (i!=p&&i!=q) { double u=a[p][i],v=a[q][i]; a[p][i]=u*cost+v*sint;a[q][i]=v*cost-u*sint; u=a[i][p],v=a[i][q]; a[i][p]=u*cost+v*sint;a[i][q]=v*cost-u*sint; } //计算特征向量 for (int i=1;i<=n;i++) { double u=EigVec[i][p],v=EigVec[i][q]; EigVec[i][p]=u*cost+v*sint;EigVec[i][q]=v*cost-u*sint; } } //对特征值排序 for (int i=1;i<=n;i++) id[i]=i,key[i]=a[i][i]; std::sort(id+1,id+n+1,cmpEigVal); for (int i=1;i<=n;i++) { EigVal[i]=a[id[i]][id[i]]; for (int j=1;j<=n;j++) tmpEigVec[j][i]=EigVec[j][id[i]]; } for (int i=1;i<=n;i++) for (int j=1;j<=n;j++) EigVec[i][j]=tmpEigVec[i][j]; //特征向量为列向量 } int main() { scanf("%d",&n); for (int i=1;i<=n;i++) for (int j=1;j<=n;j++) scanf("%lf",&mat[i][j]); Find_Eigen(n,mat,EigVal,EigVec); printf("EigenValues = "); for (int i=1;i<=n;i++) printf("%lf ",EigVal[i]); printf("\nEigenVector =\n"); for (int i=1;i<=n;i++) for (int j=1;j<=n;j++) printf("%lf%c",EigVec[i][j],j==n?'\n':' '); return 0; } ```\]
